2000-02-07[n年前へ]
■記憶の中の風景 
Photoshopで美術遊び 水彩画と色鉛筆 編
大学時代のとある日にCanon Ftbというカメラをゴミ捨て場で拾ってから、写真が私の趣味の一つになった。大学院に入る頃には、使われていなかった暗室と写真焼き付け機をも研究室の地下で見つけ、せっせと写真を焼き付けることも大好きになった。その暗室は怪人二十面相が登場しそうな古〜いレンガ造りの建物の地下にあって、実に不気味な場所だったのだが、全然気にならなかったのが今から考えるにとても不思議だ。
私が拾ったFtbはいつの間にか壊れてしまったから、他のカメラを買ったり(それでも中古だったが)、交換用のレンズを買ったりということはした。しかし、私の興味は風景や被写体の方には向いたが、カメラやレンズあるいは暗室機材といったものに対してはあまり物欲がわかなかった。
そんなことを思い出したのは、私の職場の人達がCanon EOS D30(358000円ナリ)を買ったり、EF300mmF2.8L(690000円ナリ)を買ったりと、物欲大魔人に変身していたからだ。まるで、「この世の終わりまであと一ヶ月」の「宵越しの金は持たない江戸っ子状態」で買い物をしまくっているのである。マジメに、「こ、この世の終わりが来るのですか?」とか、「あそこに見える富士山はヤッパリ噴火するのですか?」はたまた、「あなたは実はスタパ齋藤なのですか?」とかおそるおそる尋ねたくなるホドなのである。
ところで、ふと気付くと時はすでに二十一世紀になっていて、持ち歩いていたEOS620はデジタルカメラのFinePixに代わり、数学教室の地下にあった暗室はノートPCの中にあるPhotoshopに変わってしまっている。そんなことをつらつらと考えていると、ちょっとセンチメンタルな気分になったので、今回は暗室で印画紙上に浮かび上がる画像を眺めていた頃を思い出しながら、photoshopで少し遊んでみることにした。(こんなに無意味に前振りを書いたのは、そんなに大した話じゃないけどセンチな気分なのだから勘弁して欲しい、という気持ちである。)
写真というのは何の考えも無しに撮ってしまうと、不必要にリアルになってしまう。不必要にリアルということは、逆に必要なところがリアルでなくなってしまったりする。あまりにリアルすぎて、「記憶の中の風景」とは違ってしまったりするのである。そうなると、私にとってはリアルな「昔見た風景」ではないのである。私の中の記憶が間違っているといえばそれまでなのだが、私の中ではその記憶が基準なのだ。
そんな時、いっそのこと写真を絵画風に加工して、私の「記憶の中の風景」に合わせてしまおうかと思うことがある。写真を絵画風に加工するソフトというのはたくさんあるので、そんなことは簡単にできてしまう。Photoshopに含まれているフィルターでもそれっぽい(かなり不十分な機能ではあるが)ものはたくさんあるし、サードパーティー製のプラグインもたくさんある。そしてまた、インターネット上の情報でも、「絵画風&ソフトフォーカス(デタラメPhotoshop)」などがある。そんな中でも、特にこのVirtualPainterなどはかなりスゴイ。いくつかの処理ができるのだが、その中でも特にこのPlince(色鉛筆風)とRabica (水彩画風)の二つはとてもきれいである。
 |  |
 |  |
ソフトが勝手に自動変換したとは思えないくらい、なかなかスゴイできばえである。最初見たときはちょっとビックリしたほどだ。少なくとも私が色鉛筆や絵の具の筆を手にしても、こんな絵は書くことができないに違いない。いや、正直に言えば「できないに違いない」どころではなくて、「できない」のである。
ところで、このソフトはシェアウェアで、未だ購入していないので画面中に「Unregistered」という文字が恥ずかしくも輝いている。もちろん、素晴らしいソフトなので買うつもりではあるのだが、他人様の作ったソフトをただ使うのは今ひとつ面白くない。まずは、自分自身で同じようなことができるかどうか挑戦して、そしてできることならば自分の好きなような効果が出るようなプラグインなりソフトを作ってみたい。
というわけで、自分の頭を整理するために、まずはPhotoshop5.5単体を使って、この二つの処理と似た処理をしてみることにした。まずは簡単そうな水彩画風からだ。
下の写真はメキシコのティファナで撮ったよくある街並みの写真だ。何の変哲もない写真ではあるが、実はこの直後にデジカメを道路に落としてしまって、私のデジカメ様はこの後お亡くなりになってしまったという、私にとってはとても哀しい写真なのである。
 |
さて、この画像を水彩画風に変換する時の方針は、
- 色が付いてる部分は、水彩絵の具で塗りつぶす。つまり、階調性をなくして、境界はにじませる。
- 細かな部分は鉛筆で書くから、シャープに書く。
そして、水彩絵の具っぽくするために、CMYチャンネルを選択して、「フィルタ→ノイズ→ダスト&スクラッチ」をかける。そうすると、もうかなり水彩画調に感じられるようになる。そして最後に水彩絵の具のにじみを再現するために、CMYチャンネルのみに「フィルタ→表現手法→拡散」あるいは、ランダムのグレーノイズを2チャンネル分用意して、「フィルタ→変形→置き換え」でにじみを表現しよう。ちなみに、今回は「フィルタ→変形→置き換え」の方を使ってみた。ここで、「フィルタ→ブラシストローク→はね」はCMYKモードでは使えなかったので、残念ながら却下である。また、色モード変換時に彩度が低下するので、彩度アップは適時しておいた方が良いだろう。
こうして、紙の漉き目に沿った水彩絵の具のにじみも処理すると下のような画像が出来上がる。「できるかな?」の色鉛筆風のメキシコのティファナの風景である。
 |
私のセンスがいまいちなのはさておき、水彩画風にする処理としてはまぁ許せるレベルだと言えるかもしれない。処理自体は何段階もあるが、アクションファイルでも作ってやれば、簡単にできると思う。
さてさて、このイキオイで一気に色鉛筆風も片づけてしまおう。こちらの色鉛筆風の方針は、
- 画像を何色かに分解して、その色で斜線をひく。
- 色が濃い部分は別の角度からも線をひく。
- 細かい部分は黒鉛筆で少しだけシャープな線を入れておく。
まずは、まずは「イメージ→色調補整→色相・彩度」で彩度を最大にする。「イメージ→色調補整→トーンカーブ」で少し明るめの画像にする。次に、「フィルタ→ピクセレート→点描」で、何色かの色に分解しつつ、なおかつ点画像にすることであとで色鉛筆風の斜線に変形する準備をしておく。そして、「フィルタ→ブラシストローク→ストローク(斜め)」で点を斜線に変形させ、その後「フィルタ→シャープ→アンシャープマスク」をかけて、エッジをシャープにして、色も鮮やかにして色鉛筆っぽくする。また、現画像を「イメージ→色調補整→トーンカーブ」ですご〜く明るめの画像にしたものに対して、同様の処理をかけて(ただし、斜線の角度は変え)、先程の画像にαチャンネルで重ね合わせる。また、現画像を「イメージ→色調補整→トーンカーブ」でものすご〜く明るくしたものもさらにαチャンネルで重ね合わせる。
この色鉛筆風の処理のコツは点描で分解して、ストローク(斜め)+アンシャープマスクで長めの鮮やかな線にすることである。
すると、こんな感じで「できるかな?」の色鉛筆風の藤原紀香のできあがりである。Photoshop付属のフィルタだけで処理している割には、なかなか良い感じのできに思えるのだが、それは単に藤原紀香の色香に惑わされているだけかもしれない。
 |
今回は、写真画像を会画風にするためにはどんな処理をすればよいかを考えるために、Photoshopの内蔵フィルタだけを使って処理してみた。次回は、今回考えた処理の流れを自作アプリで組んでみたいと思う。そうそう、あと「こんな処理をしてみたい」という希望メールも大歓迎です。そういう希望を教えていただければ幸いです。だからといって多分何をするわけでもありませんが、ハイ。
2000-06-29[n年前へ]
■オッパイ星人の力学 
胸のヤング率編
本WEBサイトは「技術系サイト」というジャンルに分類されることが多い。が、実際にはどうも変な話題も多いように思う。しかし、私の観察によれば技術系サイトと呼ばれるところには必ずこの手の話が転がっているのである。実際、究極の技術系サイトの「Fast&First」でもというような素晴らしい話題はいっぱいあるし、同様に至高の技術系サイトである「今日の必ずトクする一言」の中でもという絶品の作品達が飾られている。
いや、つまり何が言いたいのかというと、変な話を書いてしまったことを正当化したいのである。技術系サイトには「とても身近なナゾ」への探求話が欠かせないのだから、変な話を書いたけど、勘弁しておいて欲しい、と言いたいのである。間違ってもエロサイトには分類して欲しくないのである。さて、どんな話かは下を読んで頂くことにして、もう少し言い訳を続けたい。何と言うか、この話を書き終えて何故か言い訳なしにはWEBに出せないような気持ちに、私はなっているのである。いっそのこと、この話は封印しようかとも考えた。しかし、先に示したように究極・至高の技術系サイトにもこういった?類の話があることに勇気付けられ、せっかくなので公にしてみることにした次第である。
以前、
で「できるかな?」読者の好みを調べてみた。それがこの下の円グラフである。 |
この円グラフから引っ張った部分は「エロ」である。これは、「IO = アイオー」ではない。「エロ= えろ=すけべぇ」である(前にも書いたけど)。 かように、「エロ」に興味を持つ人は多い。例を挙げるならば、「オッパイ星人」という言葉があるくらい、男の中には女性の胸に興味を持つ人が多い。私の友人の中には、ことあるごとに「おぉっ!!」と言いながら、通り過ぎる女性の胸を眺めるような輩までいるのである。しかもメガネをポケットからすばやく取り出し、サッとメガネをかけながら眺めるのである。まるで、ウルトラマンのセブンに変身する瞬間のモロボシダンなのである。「ウルトラセブンか、オマエは!」とか「モロボシダンがオッパイ星人に変身してどないすんねん!」と突っ込みたくなるほどである。
とりあえずこういう「オッパイ星人」のために、今回は「オッパイ星人の力学」について考えてみたい。具体的には、「バスト(なんか気恥ずかしいので言葉を変えた)の力学」について考えてみることにした次第である。
それでは、バストの力学について考え始めることにしよう。今回は、まずバストの基礎特性を調べ、次回にその運動力学について考えてみる予定である。
最初に、基本的な知識からだ。TVを観ていると、よく「Fカップアイドル」というような言葉を聞く。その言葉はよく耳にするのだが、実際のところその意味は知らなかった。そこで、調べてみると、ブラジャーのカップサイズは次の表のようにして決まるという。
| カップ | AAA | AA | A | B | C | D | E | F | G | H | I | J | K |
| アンダーバストと トップバストとの差 | 5.0 | 7.5 | 10 | 12.5 | 15 | 17.5 | 20 | 22.5 | 25 | 27.5 | 30 | 32.5 | 35 |
胸のバスト直下の部分の胸囲 = 「アンダーバスト」と、バスト部分の胸囲= 「トップバスト」の差からブラジャーのカップサイズが決まるわけだ(って今知っただけの知ったかぶりだけど)。Kカップなんてのもあるなんて驚きである。いやぁ、知らなかった。
しかし、「アンダーバストとトップバストとの差」が判っただけではバストの力学について考えるのは難しい。もう少し、取り扱いやすい量に変形させたい。そこで、次のような図を考えてみた。これは「胸部の断面図」である。上方向が人の前面方向である。
 |
バストを「半球状の物体」と仮定して、その「半球の半径 = r」を計算したいのである。そうすることで、バストの形状を計算しやすくなるのである。現実問題としては、バストがそうそう「半球状の物体」になるわけはないだろう。しかし、今回はとりあえず理想のドーム形状のバストを計算してみる、ということで許してもらいたい。
さて、上の極めて大雑把な近似をしまくりの図を見て頂くと判るように、
アンダーバスト = 4r + 4r + 2 胸のベース部分の厚さであり、
トップバスト = 2 r + 2 π r/2 + 4r +2 胸のベース部分の厚さである。したがって、
「アンダーバストとトップバストとの差」 = ( 2 r+2π r/2+4r+2胸のベース部分の厚さ)と計算してやることができる。そのようにして、計算した「胸のカップ数とr(cm)」を示したものが下の表である。ただし、実際には胸囲はそもそも下へ行くほど小さくなっているだろうから、アンダーバストはトップバストよりも胸のベース部分が35%小さいとして計算してみた。
- ( 4r+4 +2胸のベース部分の厚さ )
=2 r+2πr/2-4r
| カップ | AAA | AA | A | B | C | D | E | F | G | H | I | J | K |
| r | 2.8 | 4.3 | 5.7 | 7.1 | 8.5 | 10 | 11 | 13 | 14 | 16 | 17 | 19 | 20 |
これをグラフにしたものを下に示す。ほぼ直線的にバストのサイズが増加しているのが判ると思う。
 |
例えば、AAAカップだと半径2.8cmの半球状の物体だ。まるで、スーパーボールである。これなら、ブラジャーはいらないだろう。それが、Kカップともなると半径20cm程になる。ちょうどメロンを半分に切った感じだろうか?これはかなり、デカイ。
このr(cm)さえ計算できれば、あとは物体形状も体積もわかる。体積が判れば、当然のごとく重さも計算することができる。というわけで、次は重さについて考えてみよう。何しろ、バスとの運動力学を考えるならば、どの程度の質量を持つかどうか考えることは避けて通れないのである。
バストのほとんどの部分を占めるのはきっと脂肪だろう。脂肪の密度は水とほぼ同じだろう。そこで、脂肪の比重が1g/cm^3であるとして計算してやると、「胸のカップ数と胸一個あたりの重さ(g)」は以下のように計算することができる。(実はこの計算には後の松坂季美子の胸の重さに合わせるための定数、季美子定数を乗してある。)
| カップ | AAA | AA | A | B | C | D | E | F | G | H | I | J | K |
| 胸一個あたりの重さ(g) | 8.9 | 30 | 71 | 140 | 240 | 382 | 570 | 810 | 1100 | 1500 | 1900 | 2500 | 3100 |
なんと、Kカップでは「胸のカップ数と胸一個あたりの重さ(g)」が3000g= 3kg程もあるのだ。新生児が二人胸にぶら下がっているのである。この数字がホントなら大変な話だ。肩に負担がかかりんまくりである。1.5リットルのペットボトルを4本も胸にぶら下げているのだから、これは大変だ。なるほど、ブラジャーは必需品である。
上の表をグラフにしたものが下である。
 |
バストの質量は体積に比例する、すなわち、バストのサイズ( =長さ )の二乗に比例する。そこで、このような形状のグラフになるわけである。このグラフを眺めていると、Dカップ辺りを境にして、それより大きくなると胸や肩にかかる負担がシャレにならないくらいの大きさになると推測される。
ところで、地表にいる限り、当然バストも重力の影響を受ける。いや、むろん地表でなくても重力の影響は及ぼされるわけだが、そういう話は今回はおいておく。とりあえず、六本木を歩いている彼女も、ロサンゼルスにいる彼女も重力の影響を受けるのである。重力を受ければ、当然バストは重力で引っ張れる方向に垂れ下がってしまう。その様子を示したのが、次の図である。ここでは、「胴体から垂れ下がるバスト」を単純に「重りとバネで表すことができるモデル」だとしてみた。
 |
さて、一般的にバネの特性はフックの法則により
ここまで来れば、あともう一歩である。この式のkすなわち「バストに関するヤング率」を調べるだけである。「バストの垂れ具合」と「バストの重さ」を同時に計ってやれば良いのである。そうすれば、残るただ一つの変数、「バストに関するヤング率」を計算することができる。いやぁ、簡単、簡単....
といっても、実際のところここが一番苦労した。「バストの垂れ具合」と「バストの重さ」を同時に計らせてくれる人なんかどこにもいないのである。当たり前である。
そこで、ネットで検索をかけまくること数時間、ついに私は見つけたのだ。
そして、その質量 一個1kg!」
科学の徒として、私が丁寧に観察した結果、松坂季美子の「バストの垂れ具合」は約10cmであることがわかった。いや、もちろん科学の探究心のためであって、それ以外の気持ちはなかったことをここに誓っておこう。
その苦労の結晶のデータが、
- 松坂季美子はGカップ、バストの重さ=1kg、バストの垂れ具合10cm
この境界条件さえあれば、「バストに関するフックの法則」を完全に解くことができて、「バストに関するヤング率」も導き出すことができるのだ。ちょちょいのちょい、である。
その「バストに関するヤング率」を用いて計算してみた「胸のカップ数とバストの垂れ具合(cm)」を次に示してみる。
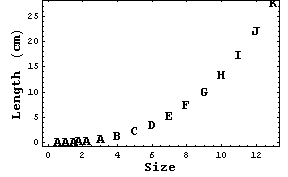 |
バストの「カップ」サイズの三乗に比例して、「バストが垂れていく様子」がよくわかると思う。この物理形状は「カップ」サイズに比例して、「バストの垂れ具合」は「カップ」サイズの三乗に比例するというデータを用いることにより、「究極のバストサイズ」を導き出せるのではないか、と私は考えているのである。が、それはまたいつかの話題と言うことにして、話を続けたい。
ところで、「バストに関するヤング率」は常に一定ではない。「おばあちゃんの垂乳根」を想像して頂けばわかるように、年をとれば「バストの垂れ具合」は大きくなるのである。
というわけで、さっきの計算結果をもっと若い条件、すなわちもっとヤングなヤング率で計算してみたのが次のグラフである。
 |
赤のもっとヤングなヤング率で計算してみた場合には、バストには張りがあって、バストの垂れ具合は小さいことがわかると思う。
さて、今回はバストの基礎特性を調べてみた。次回、この「バストに関するフックの法則」を用いて、「オッパイ星人の動力学」について考えてみたい、と思う。
追伸 : この話を書き上げた後に、恐る恐る回りの人に感想を聞いてみた。すると、
と言われてしまいました。ハイ、申し訳ありません。その通りでございます。返す言葉もありません。「こんなの作るくらいなら、
男の人のヤング率でも計算しなさいよ。」
2001-06-21[n年前へ]
■二十一世紀の「ミニスカートの幾何学」 
可愛いAIBOはちょっぴりエッチ
「面白い記事がありましたが、読みましたか?ふふっ(笑)。」というメールが先日私に届いた。さてさて、一体どんな記事だろう?うむむ…?と見に行ってみると、それはZDNNのこんな記事だった。
- 「しつけ」られたAIBO——無線遠隔操作ソフトに,盗撮防止機能
- ( http://www.zdnet.co.jp/news/0106/08/aibo.html?0b06012410 )
しかし、しかし、である。これだけでは、先のメールの書き主が私にわざわざこのニュースを知らせてくれる理由がわけ判らないではないか。私はお茶ノ水博士のようなロボット博士でもなければ、TVチャンピオン常連のおもちゃオタクでもないのである。ましてや、先のメールの「ふふっ(笑)」は奇奇怪怪としか言いようが無い。もしかしたら、これは新手のAIBOの売り込みだろうか?あのSONYもついにSPAMを出すようになったか、あのSONYがなぁ、と思いつつ記事を読み進んでいくと、記事の終わり近くになってやっと疑問は氷解したのである。その部分を少し引用してみると、
今回,遠隔撮影を可能にするAIBO Navigator開発にあたって,ソニー社内でも盗撮問題が再浮上。AIBOを担当するエンターテインメントロボットカンパニー内に「倫理委員会」を設置するなど,盗撮問題に対して真面目に取り組んだという。ということだそうだ。なるほど、これはまさにである。理系学生の憧れナンバー1といえばソニーであるが、そのソニーの「真心」とも言うべきソニーの「倫理委員会」と私は同じような「研究」をしていたわけである。「女性のためのミニスカート理論の構築を目指していた」ミニスカートの幾何学はまさに「真心・倫理」を具現化した研究と言っても良いくらいであるが、やはり判る人には判るのである。先のメールの主は私に「あなたのレポートはまさに日本の倫理のために役立っているのですよ」と教えて下さっているに違いないのである。もっとも、残念なことに私はソニーの倫理委員会と違って「短いといわれているミニスカートの丈の長さを実際に定規で測って調べたり」する機会には恵まれなかったのである。
「AIBOのアタマが,ある角度以上に上を向くと,見てはいけないものが見えてしまう」(ソニー)ということで、倫理委員会では、まず盗撮される側のデータを収集。女性の平均身長の調査から始まり、短いといわれているミニスカートの丈の長さを実際に定規で測って調べ、AIBOの頭部カメラがどの角度までなら大丈夫かをさまざまな角度から調査。その結果、可動角度を最大20度とし、首の位置が20度以上動くようなモーションをしなくてはいけないときは、動画が止まる機構までも装備した
が、そんなことはさておき、「角度で20度までなら、見てはいけないものが見えない」というのは本当だろうか?それは、ミニスカートの幾何学で調べるとどういうことになるのだろうか?というわけで、このナゾについて少し考えてみたい、と思うのである。
というわけで、まずは「ミニスカートの幾何学」の復習をしよう。ミニスカートの内側の下着が見えるか、見えないかを考えるには次のような図を考えると判りやすい。ここでは女性の真下の地点を原点にとり、水平方向にX軸をとり、鉛直上向きにY軸をとっている。
 |
スカートの内側の「見てはいけないもの」が見えてしまうのは、上の図で緑の線よりも下側に入って、その緑の線より上を見上げた場合である。そして、ここでその緑の線は
- 女性の下着の一番下の部分の位置
- ミニスカートの一番端の下の位置
それでは、その「限界角度」を調べるために、とっても簡単「ミニスカートの幾何学」を活用しよう。まずは、例えば女性のヒップ周りが88cmとしてみた場合に、スカート中央から端までの長さ(rcm)は、女性のヒップを円と近似すると、
2πr = 88cmであるから、スカート中央から端までの長さ(r cm)は
r = 14cmとなる。すると、図を見ればわかるように、緑の線 -> 「下着防衛ライン」はスカートの丈を未知数として、
y = - ((スカートの丈 - 25)/14) x + 股下長さという式で表すことができるわけだ。ここで、「AIBOがそれ以上上を向くと見てはいけないものが見えてしまう」という緑の線の角度は
ArcTan[ (スカートの丈 - 25)/14 ] / (2 π)*360で表されるから、それを計算してみて、「スカートの丈」に対する「見てはいけないものが見えてしまう」限界角度を計算してみると、その結果は次のグラフのようになる。
 |
このグラフを見れば判るように、女性のスカートが長くなれば長くなるほど、「見てはいけないものが見えてしまう」限界角度は大きくなる。当り前である。長いスカートの中を覗こうとしたら、AIBOはそのスカートの中へ入り込んで、かなりの上を見上げなければならない。もちろん、スカートの丈が短くなればなるほど、スカートの中身は覗きやすくなる。そうすると、AIBOがそれほど上を見上げなくても、「見えてはいけないもの」が見えるようになってしまうのである。
さて、前回の「ミニスカートの幾何学」では女性達が履くスカートは短くても32cmまでであって、その長さであれば角度が30°ほどにもなる急な階段でも女性のスカートの中の「見えてはいけないもの」は見えることが無い、ということを明らかにした。というわけで、それを知ってか知らずか女性達の履くスカートは短くても32cmまでなのである。だとすれば、その32cmに対応する限界角度は「見てはいけないものが見えるための必要角度」ということになるわけである。
すると、このグラフを見れば一目瞭然、スカートの下限「見てはいけないものが見えてしまう」限界角度は20数度よりも大きいことが判るのだ。ということは、先の記事の通りに、AIBOの首の上限角度を20度にしておけば、もうどうやってもAIBOはスカートの中身を覗くことができなくて、AIBOが盗撮者の手先となってしまう危険は防ぐことができるのである。それより上を眺めれば、見たことのない映像が見ることができるハズなのではあるが、ロボット三原則に基づいて(大ウソ)、AIBOの首はそれより上には上がらないように設計されているわけである。
というわけで、こんな風にソニーの「倫理委員会」がうらやましいばかりの数々の実験を重ねて調べたことも、このミニスカートの幾何学から導き出すことができるのだ。あぁ、なんて社会の役に立つ研究なのだろう。こんな女性のため、社会正義のための幾何学がこの他にあるのだろうか…。しかし、そんな社会正義のための研究だったハズなのに、この「ミニスカートの幾何学」をきっかけにしてhirax.netが色モノサイト扱いされ、さらには有害サイト扱いされるようになるとは… 思いもしなかったなぁ… ふっ… (涙)…。
2001-12-24[n年前へ]
■サンタが街にやってくる 
複数サンタクロースの巡回問題
簡易に書き直した2011年版もあります。
幼い頃、クリスマスの夜を清里の聖ルカ教会で過ごしたことがある。今では、「アイスクリーム」で有名になってしまった聖ルカ診療所の隣の教会だ。清里を通る小海線が蒸気機関車からディーゼル列車に切り替わった頃だった。私の住んでいた野辺山から一番近い病院がその聖ルカ診療所だった。今はどうなのか判らないけれど、あの病院の中の風景はまるで高原の療養所のようで(高原の診療所なのだから大して違いはないのだけれど)、とても不思議だった。
さて、クリスマスの人気者と言えば、やはりサンタクロースである。世界中の子供達から待ち焦がれられ、プレゼントを配って歩くのだから、クリスマスイヴのサンタは大忙しなのである。一体、サンタクロースはどんな風にプレゼントを配って歩くのだろう、と思った私は「サンタクロースの巡回問題」について考察をしてみることにした。
知らない人のために書いておくと、「巡回サンタクロース問題(TSP:TravelingSanta Problem)」というのは「巡回セールスマン問題(TSP:Traveling SalesmanProblem)」の特殊例である。そもそも「巡回セールスマン問題」というのは「n人の顧客の場所が与えられたとき、全ての顧客を一回ずつ経由して巡回する際に、移動距離が最小になる経路を求める。」という問題である。計算幾何分野で最もメジャーな話であって、カーマーカー特許などこれに関係するものである。つまりは、色々なものを配達する際には「配達経路を考えるのは実は結構大変なのだ」という問題なのである。
これまで「巡回サンタクロース問題」を考えた人がいなかったか、と言うとそんなことはなくて、試しにinfoseekで"サンタ"AND"巡回"で検索すると、既に素晴らしい研究がなされている。それが
- サンタクロース研究
- ( http://www.geocities.co.jp/HeartLand-Suzuran/5872/santa.html )
そこで、そんなこれまでの「巡回サンタクロース問題」に関する研究を踏まえながら、「できるかな?」ではさらに「サンタクロース巡回問題」を考え、そして、できることであればサンタの隠された真実にさらに迫ってみようと思う。「サンタクロース巡回問題」の中には、サンタクロースの真実に近づく鍵が含まれている、と私は何故か感じるのである。
まず、始めに問題提起をしてみよう。
「果たしてサンタは一人なのか?」
どのような事件においても(別に事件ではないが)、単独犯か複数犯かというのはとても重要な問題である。犯人が単独犯か複数犯かで証拠の指し示す意味は異なってくる。サンタは一人、と私たちは何故か思い込んでいるが、そんな先入観は正しい捜査のたまには捨てる必要がある。
そこで、まずはサンタの歴史から調べてみると、Santaさんの起源、クリスマスページ!によれば、サンタクロースの起源であるSt.Nicolausは西暦4世紀頃の人であるという。その頃の人口は現在よりもはるかに少なかった。それは、サンタの労働量がはるかに少なかったということだ。なるほど、この時代であれば、サンタは一人でも不思議ではないかもしれない。
とはいえ、Santaさんの起源の中の色々なサンタの目撃情報を見ると、本当にサンタは一人なのか疑問を感じるのもまた確かである。色々なサンタが目撃されている、ということはサンタは実は複数犯の可能性が高いのではないだろうか?
また、世界の人口は人口増加に示されている全世界の人口増加の様子を見れば明らかなように爆発的に増えている。ちなみに、そこに示されているグラフを対数軸にし、近似式を加えたものが以下である。
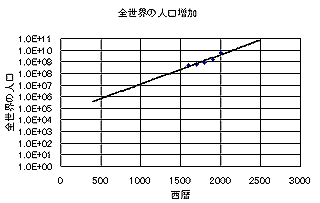 |
St.Nicolausのいた西暦4世紀頃に比べて現在の人口は4桁、すなわち、10000倍に増えている(近似式によれば。ホントのところは知らない)。これでは、サンタクロースは年々仕事量が驚異的に増えていることを意味する。もし、サンタが単独犯であるとするならば、過労死はまぬがれそうにない。
サンタの単独犯説に対する疑問は「サンタクロース巡回問題」からも示される。N人の顧客(今回の例ではN人の良い子供)が与えられたとき、サンタが計算しなければならない経路の総数は(N-1)!/2で与えられる。2で割っているのは「対称巡回サンタクロース問題(A家からB家間での距離と、B家からA家間での距離が同じという性質がある場合)」であるからだ。
子供の家N=100までの場合の、サンタが計算しなければならない経路の総数(N-1)!/2を以下に示してみる。
 |
どうだろうか、Nが少し増えると爆発的にサンタが計算しなければならない経路の総数(N-1)!/2が増えていくのがわかると思う。一軒多くなるだけで、ものスゴイ数の計算をしなければならなくなるのである。サンタが実際に配達して回るのも大変だが、その前に配達経路を決める計算量は実はもっと大変なのである。
先の人口増加の割合をこれに加えるならば、「サンタが計算しなければならない経路の総数」は天文学的数字になることは明白である。
そこで、私はやはりサンタ複数犯説が真実に近いと思うのである。サンタ複数犯説が正しいとするならば、ッ実はこの「サンタクロース巡回問題」は遥かに容易に解くことができるようになるのである。
それでは、複数サンタがいるときの「サンタクロース巡回問題」を考えてみよう。サンタが複数のm人いる場合を考える≠ニA「サンタが計算しなければならない経路の総数」はm*(N/m-1)!/2で示される。
一例として、サンタが1,2,10人の場合を示してみる。
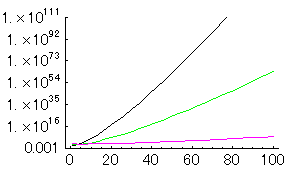 |
このグラフからサンタが複数いる場合と、単独の場合とで巡回経路を考える手間が全然違うのがわかるだろう。サンタが2人いると、計算量は半分になるのではなく、ものすごく少なくなるのである。
実際の巡回においての仕事量は、サンタがm人いれば1/mになる。しかし、その前準備はサンタがm人いれば((N-1)!/2)/(m*(N/m-1)!/2)分の一になるのだ。簡単に言えば、メチャクチャ楽になるのだ。サンタが一人では事実上サンタがプレゼントを配ることは不可能だけれど、複数犯であれば容易にプレゼントを配ることができるのだ。
このように「複数サンタクロース巡回問題」を考えることにより、サンタは複数いることが明らかだと私は思うのだ。
ただこれだけでは、不十分だ。全世界の子供達も年を経るに従って、爆発的に増えている。サンタが複数いるにしても、それでもやはり大変だ。サンタ達の人数も爆発的に増えていかなければ、とてもじゃないがやってられないことだろう。
それを解決する一つの答えはこうだ。「子供が増える割合に従って、サンタも増える」と考えるのだ。子供が一人増えると、サンタも一人増えるのだ。そうすれば、何の問題もない。子供が一人現れると、サンタも一人増えるのであれば何の問題もなくなる。
ところで、「子供が一人現れると、サンタも一人増え、サンタの数が子供と同じ比率で増えていく」ということは、子供たちがいずれサンタになるという考えが自然だとは思えないだろうか。そうだ、子供達がサンタになるのだ。子供達が大人になって、そしてサンタになるのだ。
もしかしたら、それはサンタという名前ではないのかもしれない。普段は他の名前で呼ばれているのかもしれない。けれど、クリスマスだけはサンタという名前になるのだ。電話ボックスで着替えるちょっと情けないスーパーマンのように、クリスマスイヴだけは彼らは変身するのだ。
こうして、サンタ達は子供の枕元にやってくる。むかし子供だったサンタ達が子供達の枕元にやってくる。そして、夢を見ている子供達が起きてしまわないように、そっと枕もとにプレゼントを置く。
サンタなんかこれまで私の枕元には来なかった、という人たちも多いのかもしれない。けれど、きっと、そんな人たちもまたサンタになっていくのだろう、そして、その時、本当にサンタがいる、ということに気づくのだろう。
2002-06-02[n年前へ]
■職場のスフィンクスの名台詞 
止まったエスカレーターに何故上手く乗れないのか?
ある朝、いつものように出社すると、いつもと違うことがあった。職場へ行くために通らなければならないエスカレーターが動いていない。エスカレーター横のガラスが割れているため、それを直すまではエスカレーターを止めたままにしているらしい。かなり、不便ではあるが、壊れたモノはしょうがないのである。しょうがなく、建物の端にある階段をエッチラ、オッチラ上って職場の居室へ行ったのである。 |
きっとスカレーターはすぐに直るだろうと思っていたのだが、残念ながらエスカレーターは直る気配が全く無いまま数日過ぎた。いつまでたっても、いぜんとしてエスカレーターは停止したままなのである。しかし、私たちの職場にはそのエスカレーターを使わないと辿り着けないので、その職場の人達はその止まったままのエスカレーターをいつしか階段代わりに登り降りするようになっていた。止まったエスカレーターは「楽ちんなエスカレーター」ではないけれど、ただの階段としては十分使える、というわけだ。
ところが、である。ただの階段と違って、何故か止まった「エスカレーター」は歩きづらいのである。特に、エスカレータに乗る最初の一歩がなんとも上手くいかないのだ。よく、エスカレーターに乗る最初の一歩や、エスカレーターから降りる最初の一歩が上手く出せない人がいるが、ちょうどあんな感じになってしまうのである。普段、動いているエスカレーターを使う分には、私は「上手く乗れない」なんてことは全然無いのだけれど、何故か止まったエスカレーターに足を踏み出そうとすると、体のバランスが崩れてしまうのだった。もちろん、エスカレーターが止まっていることも、微妙に段差が違うことも判っているのだけれど、だけれども何故かバランスを崩してしまうのである。
というわけで、私も含めてあらゆる人達がスカッスカッと何故かバランスを崩しながら、止まったエスカレーターに恐る恐る足を踏み出していたのである。
そんなある日、止まったエスカレータの横にシミュレーションプログラム作成を生業とするN氏がいつまでも立っていることに気づいた。そして、止まったままのエスカレーターを登り降りしようとする人達を次から次へとつかまえては、N氏は何事かを喋りかけているのである。何故だか、N氏は通る人通る人に何かの言葉を発しているのであった。それはまるで、ピラミッドの前に佇み、そこを通る旅人達に謎かけをするというスフィンクスであるかのようだった。
もちろん何処へ行くにもその止まったままのエスカレーターを使わなければならないので、私もすぐにN氏改めスフィンクスに捕まってしまうこととなった。そして、N氏はこう言ったのである。
「止まったエスカレーターに足を踏み入れるとき、何故だか体のバランスが崩れるような気がしないか?オマエは?」もちろん、それは私も不思議に思っていたわけで、
「そー、そー、そうなんですよねー。ただの止まったエスカレーターなんだから、普通の階段みたいなものなのに、不思議ですよねー。」と私が答えると、
「喝〜!不思議ですよねー、じゃぁないだろー。何故?どうして?を追求するのがオマエの仕事じゃないのかー!」と怒るのである。そ・それは私の仕事ではないのじゃないだろうか…、百歩譲ってそれが趣味なら確かにそうかもしれないが…、ワタシは別に子供電話相談室ではないんだけどなー…、と私が心の中で考えていると、
「ちゃんと、物事にはすべて原因があるハズだぁー。止まったエスカレーターに足を踏み入れるとき、何故体のバランスが崩れるのか、その理由を考えてみろー。」と怒りまくるのである。ここまでくると、ピラミッドの前で謎かけをするスフィンクスそのものである。いや、むしろそれよりタチが悪いかもしれない。何しろ、このスフィンクスはシミュレーション・プログラムを作るのを仕事にしているのだから、物理と論理に長けているのである。だから、きっと結構素朴であろう元祖スフィンクスよりなおさらタチが悪いのだ。
う〜む、これはそう簡単にこのスフィンクスからは解放されそうにないな〜、と思いながらも、私が
「う〜ん、エスカレーターが止まっている、って判っていても、無意識のうちに体がエスカレーターが動いていると思いこんじゃうんですかね〜。それで、何かバランスを崩してしまうんですかね〜」とあいまいに答えると、
「違〜う。答えはちゃんとすぐ目の前にあるのに、それにオマエは何故か気づいていないだけなのだ〜」と、スフィンクス、じゃなかったN氏はものすごく嬉しそうに叫ぶのだった。そして、そのスフィンクスは驚くべき解説を始めたのである。
「オレ達はエスカレーターが止まっている、という大きなことに気をとられて目の前、いや足下と言った方が良いか、の大事なことが見えていないんだよ。ホラ、エスカレーターの動く階段部分の直前がどうなっているか、良く見てみろよ。そこだけ傾いて斜面になっているだろう?」「あー、確かにそーですねぇ〜」「確かにそーですねぇ〜、じゃねぇよ。エスカレーターに乗ろうとするときに、俺たちの体を支えている足はそのちょうど斜面の上に乗っかっているわけだよ」「…」
 |  |
「だから、エスカレーターに足を踏み出そうとする瞬間、実はオレ達の体はエスカレーターの方に傾いてしまっているわけだ。だけど、オレ達は- エスカレーターが止まっている - ということに気をとられて、斜面の上でオレ達の体がすでに傾いてしまっていることに気づかないわけさ」このN氏改めスフィンクスが語る話を聞いたときに、ワタシは目からウロコが落ちるような気がした。そして、ワタシの頭の中で加納朋子「ななつのこ」冒頭の台詞の文章「オレ達が止まったエスカレーターに足を踏み入れるとき体のバランスが崩れるのは、踏み出したオレたちの足に原因があるわけじゃなくて、もう一方の足下が傾いているということに気づかないことが原因なわけだ」
「答えはすぐ目の前に書いてあるのに、オレ達はただそれに気づかないだけなんだよー」
いつだって、どこでだって、謎はすぐ近くにあったのです。何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。が流れ出したのである。何もスフィンクスの深遠な謎などではなくて、職場の壊れたエスカレーターの前でも謎(大切かどうかはともかく)はいくらでも日常にあふれていて、そして時には誰かがスフィンクスに変身して、その謎に答えを出してくれるのであった。なるほど、なのである。
そして、「動く階段部分の直前にある斜面」を意識するようになった途端、止まったエスカレーターでも何の問題もなく乗れるようになり、むしろ、どうしてあんなにスカッスカッとバランスを崩していたのか不思議に思えるほどになったのだった。
で、その後スフィンクス改めN氏と「動く階段部分の直前にある斜面」のその他の効果、止まったエスカレーターに足を踏み入れるとき体のバランスを崩してしまうということ以外の効果、についてしばらく話をした。で、数日後成田で「動く歩道」の上を歩きながら、その効果を確認したので、その内容を書いてみる。
 |
上の写真は平らな「動く歩道」だが、この場合にも先の場合と同じように、「動く歩道部分」直前は斜面になっている。そして、私たちは「動く歩道」に片足を踏み出すとき、もう一方の足は必ずその斜面部分に立っている。それは、ちょうど跳び箱を飛ぶ前に必ず私たちが踏切板を踏み込む瞬間のようなのである。すると、斜めになった面に片足で立った私達は、それに気づかないまま無意識のうちに体が前に倒れ、加速するのである。もちろん、斜面を片足で後ろに踏み出す効果もあって加速するのである。
私達が普通に歩いている状態に比べて、「動く歩道」の上を歩く状態というのは、私達の体の速度は速いのである。だから、普通に歩く状態から「動く歩道」の上を歩く状態にスムースに移行するためには、私達はその瞬間に「動く歩道」の速度に応じた若干の加速をしてやらなければならない。ところが、「動く歩道部分」直前の斜面のために、無意識のうちに私達はその加速を行ってしまうのである。だから、比較的スムースに「動く歩道」の上に移動して、しかもその瞬間の不連続な速度変化を感じずに済むわけだ。
そして、「動く歩道」を降りるときには、これとは逆のことが生じる。つまり、通常の歩道部分に踏み出した片足が、斜面部分に着地し、その斜面が私達の方に傾いているため上り坂を上るような状態になって、自然と私達の体は減速するのだ。だから、「動く歩道」から普通の歩道部分への移行がスムースになる、というわけなのである。
このような効果が誰にでも起きるのかどうかは判らないし、仮にそれが一般的に起きる現象だとしても、それが制作者達の意図したものであるかどうかは判らない。しかし、止まったエスカレーターを前に当惑したことのある人や、あるいはいつもエスカレーターや「動く歩道」に上手く乗れない人は、ぜひ「動く部分直前の斜面」に気をつけながら、足を踏み出してみてもらいたい、と思うのだ。
それにしても、「答えは目の前に書いてあるのに、オレ達はただそれに気づかないだけ」とは、ミステリー小説の中の気持ちの名探偵の台詞のようである。色んなところで色んなことで、私達はよろめいたり、つまづいたりするけれど、そんな時目の前の景色や、足下の景色をじっと眺めてみれば、目の前にその答えが大きく書いてあったり、あるいは転がっていたり、そして時にはその答えを踏みつけていたりするものなのかもしれないな、とふと思ったりするのである。だけど、やっぱり私達はそんな答えには気づかないまま、無意識に体が傾いてバランスを崩してしまうのかもしれないな、と思ったりもするのである。
