1999-11-23[n年前へ]
■ミニスカートの幾何学 
32cmの攻防戦
早朝、東名高速で事故渋滞にはまってしまった。仕方がないので、TVを眺めていると、面白い話をやっていた。それは、ミニスカートの丈の話である。何でも、最近の流行はミニスカートの丈が32cmのものであるらしい。女子高生?などが言うには、
「34cmだと長いしぃ。」だから、32cmだと言うのだ。別に、オリンピック選手でもないのだから、ミニスカートの丈の限界まで挑戦しなくても良いだろう、と私などは思ってしまう。しかし、彼女たちはそう考えないらしい。人それぞれである。
「30cmだと下着が見えちゃうしぃ。」
それにしても、スカートの丈が32cmと30cmの間でそんなに、違いがあるものだろうか? 「見える・見えない」を決める分水嶺がその2cmの違いにあるものなのだろうか? 妙に不思議である。 そこで、ミニスカートの幾何学について考えてみることにした。題して「32cmの攻防戦」である。
何より先に確認しておくが、私は今回は科学的好奇心で動いているのである。そこに、一点の不純な気持ちも存在しないことを、ここで確認しておく。いや、むしろ、女性のためのミニスカート理論の構築を目指しているといっても良いかもしれない。といっても、信用されないとは思うのであるが...
 |
さて、先のTV番組によれば、腰からスカートの先までの長さを「スカートの丈」というらしい。また、先のTV番組により、「腰から下着の一番下の部分(股下を計るときの一番上)までの長さが大体25cmである」という重要な情報を得ることができた。
それでは、解析を始めてみよう。以下に、今回考えた「ミニスカートの幾何学」を示す。なお、今回使用する長さの単位は全て(cm )である。
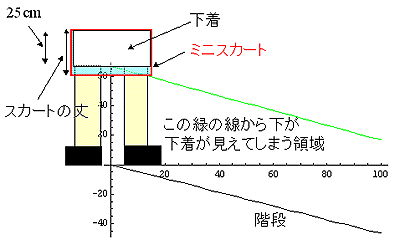 |
まず、階段の途中に立つミニスカートを履いた女性の下着中央部分とミニスカートの最下部を結ぶ直線を考える。この線よりも下が、下着が見えてしまう領域である。もちろん、階段の下には潜り込めないわけであるから、その線と階段で囲まれた領域内から見た際に下着が見えてしまうわけだ。その線のことを「下着防御ライン」と呼ぶことにする。
さて、ミニスカートの形状を考えよう、スカートの丈はもちろん入力条件としてわかる。すると、足りないパラメータは幅である。そこで、ヒップ周りが88cmとしてスカート中央から端までの長さ(rcm)を求める。2πrが88cmであるから、
r = 14cmとなる。
また、駅などの階段というと25度位だろうか。30度というとかなり急な階段である。湘南通商の階段とか急な階段は色々あるが、今回は急な階段の斜度として、25-30度位としておく。ちなみに、京都駅北口のエスカレータで実測したところ、25,6度であった。
それでは、スカートの丈が32cmで階段の角度が30度である場合の計算をしてみる。女性の股下は仮に70cmであるとしておく。おそらく、身長160cm位であれば、この程度であろう。
それでは、ミニスカートの丈が32cm、30cmの時の「下着防御ライン」を計算したものを示す。
 |  |
緑、すなわち、ミニスカートの丈が32cmの時は「下着防御ライン」は階段とほぼ平行である。それに対して、丈が30cmの時の「下着防御ライン」は、ミニスカートを履いた女性から離れるほど階段よりも上に離れていく。ということは、人間の視点位置が「下着防御ライン」を越えるということである。すなわち、下着が見られてしまうということだ。
階段と「下着防御ライン」の差、すなわち、人の目の高さがこの程度ならミニスカートの下の下着を見ることができる、というものを示してみる。
 |
32cmの丈の場合、10m(1000cm)離れても、目の高さが150以下の人しか「下着防御ライン」を突破できない。すなわち、女性は事実上「下着を見られる恐れがない」といって良いだろう。もちろん、20mとか離れたら別である。しかし、超人的な視力がなければ、そのような条件下で下着を確認することはできないであろう。
それに対して、30cmの丈の場合には6m離れた時点ですでに視点が2mの位置にある人でも「下着防御ライン」を突破できてしまう。これでは、「全ての人に下着を見られてしまう」ということになる。
もし、女性の身長が20cm程度高く、180cm程度であったら、どうなるだろうか。おそらく、股下長さは10cm程度長くなる。すると、上の図(階段と「下着防御ライン」の差)の緑、赤ラインは10cm程度高くなる。それでも、緑の32cmスカートの「下着防御ライン」はやはり安全圏といえるだろう。
また同様に、厚底サンダル・ブーツなどを履いた場合には股下長さが20cm弱高くなると考えられる。この影響を考えると、長さとしては身長の影響よりも大きいわけである。それは、身長の1/2が股下長さの増加に繋がるのに対し、厚底靴の長さはそのものずばり股下長さの増加に繋がるからである。しかし、それでもやはり緑の32cmの「下着防御ライン」は安全圏である。
すなわち、32cmと30cmのスカートの丈の長さの間には、「下着が見える・見えない」に関する分水嶺が確かに存在するのだ。先の、
「30cmだと下着が見えちゃうしぃ。」という発言は理論的に裏付けられたのである。
それでは、次に階段の角度が25度である場合の計算をしてみる。
 |
緑の線、すなわちスカートの丈が32cmの場合の「下着防御ライン」が階段にどんどんすり寄っているのがわかると思う。すなわち、「下着防御ライン」はより強固なモノとなっているのである。階段と「下着防御ライン」が女性から離れるほど近づくのである。次に、階段と「下着防御ライン」の差を見てみよう。
 |
緑線、すなわちスカートの丈が32cmの場合に注目する。 女性から、離れても、近づいても、何人たりとも、下着を見ることはできないのだ。下着がシュバルツシルト半径の中に隠されるといっても良い。女性の安全を確保する「完全安全条件」を満たす「下着防御ライン」が完成されているのだ。
これは階段と「下着防御ライン」が平行である条件を境として、そのような条件が達成される。その条件よりより「下着防御ライン」が強固になると、誰も「下着防御ライン」を突破することはできない。すなわち、「完全安全条件」が達成されるのである。
この絶対に下着を防御可能(「完全安全条件」)な「完全安全条件」とは、階段と「下着防御ライン」が平行である条件であるから、ミニスカートの丈(xcm)をパラメータとして、
Tan[階段の角度] = (x-25)/14で計算することができる。ここで、14は腰回りの半径(cm)であり、Hip88cmの人の場合である。もちろん、極端な安産体型の場合には、その14という値を適当に補正する必要がある。
さて、この条件には女性の身長(股下長さ)は関係しないところが面白い。もちろん、厚底サンダルなどを履いても同じである。もちろん、若干の影響はあるが、あまり影響はない。
さて、今回の「ミニスカートの幾何学」の考察により、判明した結果をまとめてみよう。
ミニスカート内部の下着が「見える・見えない」には
- ミニスカートの丈が30cmと32cmの間に、分水嶺が確かに存在する
- 絶対に下着を防御可能(「完全安全条件」)なミニスカートの丈(x cm)とは、Tan[階段の角度]= (x-25)/14 により決定される
- ここで、14は腰回りの半径(cm)であり、Hip88cmの人の場合である
- 極端な安産体型の場合には、その14という値を適当に補正する必要がある
- 一方、ミニスカートを履いている人の身長はほとんど影響を及ぼさない
- 厚底サンダルの方が身長よりは影響を及ぼすが、それでもほとんど影響はない
ミニスカートを身につける女性の経験に基づく、「30cmだと下着が見えちゃうしぃ。」理論はなかなか正しいことがわかる。経験というものを軽んじてはいけない、という良い?例かもしれない。結果の伴わない理論に価値はない、ということだろうか。
それにしても、厚底ブーツにミニスカートを履いた女性達は、ロールプレイングゲームの主人公達のようだ。色々なアイテムを手に入れ、冒険を続けている主人公達のようである。ほんの少しだけ、うらやましいような気もする。
さて、こういう話題を書くと少し不安がある。もちろん、私もミニスカートを見ると、妙に心が落ち着かないのも確かに事実ではある。しかし、だからといってことさらに興味津々というわけでもない、と思う。多分。ということで、「できるかな?」の女性読者の数が減少しないことを、ただ祈るのみである。
2000-07-18[n年前へ]
■モザイクの向こう 
隠しているから良いのです
「できるかな?」への質問?で、同じような内容のメールを頂くことがよくある。その内の一つは、
感温液晶の入手先を教えて下さい。というものである。何か不思議な気がするのだが、けっこう感温液晶を欲しいと思う人がいるらしい。しかも、そのような人はインテリア関係を扱う人が多い。「人のぬくもり」を感じさせるものを作りたい、というわけのである。これを逆に言えば、「人のぬくもり」を感じさせないものが世の中には溢れているということなのだろう。液晶という実に物理的なものを通して「人のぬくもり」を感じることができる、ということが実に不思議で同時に爽快でもある。
さて、私自身は新宿の東急ハンズで感温液晶を購入したのだが、その人達のメールによれば、最近はどうも置いていないらしい。仕方がないので、
- 日本書籍 後藤富治 村上 聡 著 おもしろ科学モノ情報 200選 2000年版
感温液晶シートですが、実験材料でなくて遊ぶのにという返事を最近は出すことにしている。
使うのでしたら、光洋 03-3212-1571にあるようです。
日比谷パークビル9F
平日8:30-5:30
JR有楽町駅近く
 |
そういうわけで、こちらの感温液晶の入手方法に関するメールの方は良いのだが、もうひとつのよく頂くメールの内容がある。こちらの方はメールを頂いても、返事ができるわけでもなく、いつもそのままになっていた。その内容はと言えば、
画像処理と言えば、まずはAVのモザイクの消し方を研究して下さい。というものである。AVのモザイクというと、あの映してはマズイ部分を隠すアノ画像処理のことだろう。本来のモザイクという言葉のモノだけではなくて、アノマズイ部分を隠す画像処理一般について、それをどうにかして欲しい、と言っているのだろうと思う。
しかし、そう言われても困ってしまう。もちろん、私は「見えないもの」を「見える」ようにするのは大好きであるし、趣味でも仕事でも、「見える?見えない?」の境界線に興味を惹かれ、日夜考え続けている。だから、AVのモザイク〜マズイ部分を隠すアノ画像処理〜のようにわざわざ「見えない」ように細工をされてしまうと、それを何とか「見える」ようにしたいという気持ちが無い、と言ってしまうと嘘になるだろう。
しかし、残念ながら、このAVのモザイクの件に関しては「見えない」方が良いと思っているのである。それは、私の好みの根幹に関わる部分なのであるが、ダラダラと言い訳を書いても仕方がない、やはりここはFAQに対しての答えを用意しておくべきだと考えて、ここに簡単な説明を書いておくことにした次第である。
まずは、代表的なマズイ部分を隠すアノ画像処理の種類を示してみたい。次に示す画像は左から、
- オリジナル
- オリジナルに「モザイク」をかけたもの
- オリジナルに「ぼかし」をかけたもの
- オリジナルに「塗りつぶし」をかけたもの
 |  |  |  |
この3つのマズイ部分を隠すアノ画像処理のなかから、今回は
- オリジナルに「モザイク」をかけたもの
- オリジナルに「ぼかし」をかけたもの
さて、まずは「モザイク」に挑戦してみたい。試しに、ミロのヴィーナスのヌード画像に対して、「モザイク」をかけてみよう。次に示すのが、とあるヌード画像に対して「モザイク」をかけたものである。
19kB  | 1kB  |
GIF画像ということで圧縮もかけてあるため、一概に比較はできないが、オリジナル画像が19kBであるのに対して、右の「モザイク」画像は1kBしかない。つまり、情報量がおよそ1/20であるわけだ。それもそのはず、上の「モザイク」画像は実はオリジナル画像を単に縮小したものを拡大表示してみたものである。情報量が少なくなるのも当然だろう。
19kB  | 縮小したもの(GIF画像) 1kB | 単に拡大表示したもの 1kB  |
それでは、画像の情報量が減ってしまっている場合に、元の画像を復元することはできないのだろうか?いや、ハッキリと言えばヌード画像に対して「モザイク」がかけられてしまったとしたら、その「モザイク」の向こうのヌード画像を拝むことはできないのだろうか?
それが実はできるのである。その証拠に巷には「AVモザイク消し器」というものが溢れている。また、そんな大層な機械でなくても、巷には「モザイク」の向こうを見通すノウハウという秘伝が伝えられている。例えば、私がリサーチした限りでは、
- TVの前に半透明のシートを張る
- 目を薄開きにして、TV画面を見る
その原理とは「オリジナルの画像の性質を考える」ことである。先のオリジナルのヌード画像をじっくり見ればわかると思うが、ヌード画像というものは割合滑らかである。マッチョなヌード画像ならばいざしらず、少なくとも女性のヌード画像は普通滑らかな画像であるわけだ。当然である。だとしたら、その性質をフル活用してやれば、「モザイク」の向こうのヌード画像を拝むことができるのである。
もう少しわかりやすく言うと、こんな感じだ。まずは、滑らかなグレイスケールの画像に「モザイク」をかけてみよう。
| オリジナル | |
| 上の画像に「モザイク」をかけたもの |
すると、元のオリジナル画像は極めて滑らかな画像であるのに、下の「モザイク」をかけた画像は「モザイク」のせいで滑らかでなくなってしまっている。だとすれば、「モザイク」画像を滑らかにしてやれば、元のオリジナル画像っぽくなるのではないだろうか?周囲の画像を考えながら、滑らかな画像にすれば良いのではないだろうか?具体的に言えば、注目画素の周囲で平均値などを計算してやればよいのだろう。つまり、「ボカシ」をかけてやれば良いのである。「ボカシ」をかけると画像はソフトで滑らかになる。「モザイク」をかけた画像が滑らかでなくなってしまっているのを、「ボカシ」をかけることで滑らかにして、元の画像っぽくしてやれば良いのだ。
先の秘伝
- TVの前に半透明のシートを張る
- 目を薄開きにして、TV画面を見る
例えば、上の「モザイク」画像にぼかしをかけたものを次に示してみよう。「モザイク」画像にぼかしをかけることで、元のオリジナル画像に極めて近い画像になっていることがわかると思う。
| オリジナル | |
| 上の画像にモザイクをかけたもの | |
| モザイク画像にぼかしをかけたもの |
これが、いわゆるひとつの「モザイク」の向こうのヌード画像を拝む秘訣なのである。試しに、先のとあるヌード画像に対して「モザイク」をかけた画像を「ぼかす」ことで「モザイク」の向こうのヌード画像を拝んでみたのが次の画像である。「モザイク」画像よりはオリジナル画像っぽいことがわかると思う。
| オリジナル | オリジナル画像に モザイクをかけたもの | モザイク画像に ぼかしをかけたもの |
 |  |  |
さて、それでは逆にオリジナルに「ぼかし」をかけることでマズイ部分を隠すアノ画像処理をした場合はどうだろうか?この場合は「モザイク」の向こうのヌード画像を拝むことはできるだろうか?
といっても、こちらは以前
で扱っているので、ここでは詳しく書かない。ぼけた画像は例えば、- ウィーナ・フィルタ
- ハイパス・フィルタ
と書くだけでも何なので、試しに、Photoshopのカスタムフィルタで簡単な「ボカシ復元用フィルタ」を作成してみたものをここにおいておく。Photoshopユーザは試してみると面白いかもしれない。
このカスタムフィルタの内容はごく簡単なオペレータ演算で、次の図に示すようなオペレータ演算子を用いたフィルタである。 |
試しにこのカスタムフィルタを用いて、とあるヌード画像に対してかけられた「ぼかし」画像の向こうのヌード画像を拝んでみたのが次の例である。ちなみにここでの「ぼかし」はPhotoshopでガウス「ぼかし」の半径4ピクセルの設定でフィルタをかけてみたものだ。
| オリジナル | オリジナル画像に ぼかしをかけたもの | ぼかし画像に 先のカスタムフィルタをかけたもの |
 |  |  |
こんな簡単なカスタムフィルタでもとあるヌード画像の「ボカシ画像」を鮮鋭化できて、その「ぼかし」の向こうのヌード画像を拝むことができることが判ると思う。
実際に、私がネット上で膨大な数のエロ画像、いや違った「ボカシ」画像だ、を収集し試した結果ではかなりの割合の画像に対して、驚くべき効果を挙げることができた。本WEBに訪れるような方のほとんどには当然の知識だとは思うが、もしもこういった処理をかけたことのない方がいらっしゃれば、是非一回挑戦しみてもらいたい。特に素人ヌードの「ぼかし」画像がお薦めである(あくまで復元効果の大きさに関してだけど)。
さて、ここまで書いてから言うのはどうかと思うのだが、以前
でも書いたように、私は「素晴らしい芸術は完全な自由の中では生まれない」と思っている。それと同じで、制限の中で表現する方が実は素晴らしいものができると思っているのである。それは、私服の女子高生には心ときめかないが、制服の女子高生には思わず目を惹かれるのと同じである。完全に何でもありの私服だと実はそう簡単に輝かないのだが、制限のかかっている制服だと何故かとても輝いてしまうのと同じだ。私などは、通っていた高校が制服がなかったため、思わず同級生に「セーラー服を着て来てくれぇ」とリクエストをしてしまったくらいである。あれ、何の話だっけ...そう、つまりわざわざ隠してある部分を眺めてみることは良いとは思わないのである。隠してあるものは、隠しておいたままにしておいた方が良いのではないか、と思うのである。
そう言えば、先ほど「ミロのヴィーナス」の画像用に表紙を使わせて頂いた細野不二彦のギャラリーフェイクの中では、主人公藤田が、
「ミロのヴィーナスは腕が隠されているからこそ、人々の心を捉えたんじゃないですかね」というようなことを言う。私も本当にそう思う。
 |
「ミロのヴィーナス」の存在しない腕を想像することで、現実には作りえない理想の姿を、その像を見る人々は感じることができるのだろう。隠してあるからこそ、良いのである。
あまりに緻密に描写した弟子に「言い仰せて何がある」と言ったのは松尾芭蕉だったはずだ。想像する余地を残して、現実よりもさらに大きいものを表現した方が良い、ということである。私も本当にその通りだと思う。ある一部分だけを切り取ってその部分だけを見てみて、後は想像力におまかせというのが、私も表現としては一番良いと思うのである。もちろん、全ての人の想像力を越えるものを表現する力があるというならばともかく、そんなことができないのならばわざと一部分だけを表現するのが一番良いと思うのである。
いや、だからって別に私が変な想像をしまくりってわけじゃないとは思うけど。かといって、私が想像力とか好奇心が少ない方かと言われると...うーん...
2000-12-24[n年前へ]
■A型vB型・大戦争 
血液型分布を眺めてみよう
今年も私の職場には新入社員が入ってきた。その新入社員の中の一人は「血液型+ 動物占い」の信者だった。何しろ、ことあるごとに「血液型 + 動物占いの結果が同じ人はとってもよく似ているんですよ!もうビックリするくらい当てはまるんですよ!もちろん、たま〜に例外の人もありますけど。」といつも私たちに言うのである。もちろん、私も含めてその周囲の人は「その自信と根拠は一体どこからくるんだぁ!」とツッコミを入れるわけであるが、少なくとも本人は気持ち良いくらい自信満々なのである。とはいえ、私も占いというものは「根拠無しにテキト〜に何かを決めつけることができるという素晴らしいもの」だとも思うので、まぁそれはそれで楽しいわけだ。そんな血液型大好きな新入社員なら可愛いものであるが、それがもう少しエラ〜イ人になるとちょっとばかり大変である。私のとなりの部署の部長なども実はそんな血液型信仰者なのであるが、その部の配属には血液型が参考にされるというオソロしくも確かな真実がある(ホントにホント)。そこの某部長曰く「B型は実験が杜撰だから嫌い。」という実に誠実な理由に基づき、その部はA型人間大集合なのである。というよりも、その部からB型は外されているのだ。恐るべき純血追求型人事手法である。ヒットラーもビックリである。
そんなA型人間大集合の部がある一方で、私が所属している部屋(課)は何故かB型が多い。10人強の中で半数程がB型なのである。どこで読んだのか忘れたが、日本人の血液型はA型35%,B型 25%,AB型 10%,O型 30%位であるらしいから、私の課のB型比率はかなり高い。しかし、もちろんそれは単なる偶然だろう。隣の部がB型を排除しているから私の部屋がB型で溢れているのじゃないか、という恐ろしい想像ができないこともないが、そういうわけでもないだろうと私は信じたい。
しかし、「信じたい」という気持ちだけで物事を決めつけるのは危険この上ない。それは「セーラー服の女子高生はみんな可愛くて純真だと信じたい」という危険さと同じくらいデンジャラスである。何事も、先入観で判断してはイケナイのである。確認することが重要なのだ。そこで、今回は「10人強の中で半数程がB型なんていうのはよくある偶然」だということを血液型分布・配置シミュレーション(超手抜き)でも行って確認してみたいと思うのである。そして、私が所属している部屋(課)にB型が多いのがただの偶然であること、つまりある特定の血液型の人間が集まることが不自然ではないことを確認してみたいのである。
さて、今回の血液型分布・配置シミュレーションのやり方は次の通りだ。
- まずは256人の人間を用意する。
- その256人に対して、A型 35%,B型 25%,AB型 10%,O型 30%位になるようにAB型の抗原(AA,AO,BB,BO,AB,OO型)を配置する。
- その後、遺伝子を移動して血液型を再配置する。
- 近所の人間と子供を作る(遠距離恋愛は考えない)。
- 血液型分布・配置を調べる。
この説明の中で、一言で「遺伝子を移動して、近所の人間と子供を作る」と書いたが、もちろんその現象の中には
- 人が引っ越したり・移動したりしていったり、
- 愛が芽生えて子供がデキたり、愛が芽生えないけどデキちゃったりして子供が出来たり、
まぁ、しかしカマキリのようにエッチのあとにメスがオスを食べちゃう動物もいたりするのだし(実際のところは知らないけど)、この恐怖の「子供が一人出現すると親が一人消えてしまう」システムもそんなに不自然ではないのである、ということにしておこう。というわけで、いつもながらの強引な展開だ。
そんなわけで、行ってみた血液型分布・配置シミュレーションの結果が下の動画である。一マス一マスが一人の人間である。時間毎にどんどん血液型分布・配置が変化していく様子が判ると思う。ちなみに、
赤 = A型、緑 = B型、水色 = AB型、紫 = O型である。
 ファイルサイズがデカイのは直すつもり… |
この結果はカラフルにただチカチカするだけの計算結果ではないのである。このチカチカこそが人生の喜怒哀楽なのだ。そこを是非とも心して眺めてもらいたい、と切望する次第である。
じゃぁ、時間を追ってA型、緑 = B型、青色 = O型、紫 = AB型(色が一部さっきと逆転していることに注意)がどう変化していったかというと下の図のような感じだ。それほど一定ではないことがわかるだろう。それぞれの血液型の比率が逆転したりする下克上な瞬間だってままあるのである。
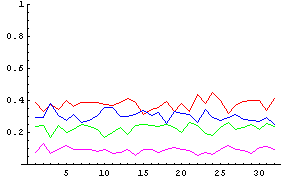 A型、緑 = B型、青色 = O型、紫 = AB型 |
もちろん、これは256人という少ない人数だからこんなに大きく比率が変動するわけである。しかし、今回は「つまりある特定の血液型の人間が集まる」かどうかを調べたいのである。つまり、ある少人数の人間達を考えたときに特定の血液型の比率が多くなることがあるかを調べたいのだから、考える人数は少人数で構わないわけだ。
256人という比較的多い人数を考えた場合ですら、人生のドラマが続く中でそれぞれの血液型比率は結構変化して、それぞれの血液型の比率が逆転したりすることもあるわけだが、じゃぁもっと狭い領域に注目したらどうなるだろうか?例えば、下の瞬間の血液型分布・配置を眺めてみよう。
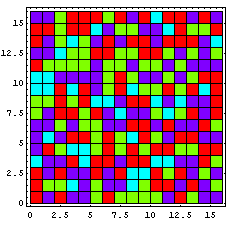 |
おやおや、結構
- A型 = 赤が連続していたり
- B型 = 緑が集まっていたり
- O型 = 紫が多いくせに固まっていたり
- AB型 = 水色が少ないながらも集まっていたり
試しに、先程のシミュレーションである16人(つまり私の部屋(課)の人数位だ)を抽出して調べたときに、A型が一番多かった場合と、一番少なかった場合で、A型の割合だどんなだったかを調べてみたのが次に示すグラフである。ここで、
- 赤 = その瞬間にA型が一番多かったグループにおけるA型の比率
- 青 = その瞬間にA型が一番少なかったグループにおけるA型の比率
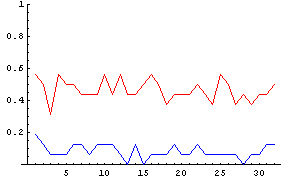 赤 = A型が一番多かったグループにおけるA型の比率 |
なるほど、A型が一番多かったグループではA型の比率が60%を越える時もある。逆にA型が少ないグループでは16人のなかにA型がいない、という状況すらあるのだ。
ということは、私の部屋のB型がほぼ半数という状態だって別に不自然ではなく、それはごく自然なわけだ。もちろん、A型とB型の比率が違うことを考慮しても、全然不自然ではないだろう。ということは、血液型信仰者の某部長による隣の部のB型キライの恐るべき純血追求型人事手法の余波をうけて、私たちの部屋がB型だらけということはなくて、それは単なる偶然だろう、ということがわかるわけだ。
ところで、ここまで書いて「血液型信仰者の某部長」が「ヘンな人」というイメージを持たれてしまうと非常に困る。何故なら、もっと変でなおかつエライ人がイッパイいるのである。(ここでいう「エライ」は関東弁&関西弁のニュアンスだ。つまり、「偉いけど大変な」というニュアンスだ。)血液型信仰者なんてカワイイもんじゃないの、と思えるくらいのスゴサである。だって、ダウジングが超大好きで、奇跡の水が超〜大好きな人だっているのだ。もしかしたら、ダウンジングなんて言葉を知らない人がいるかもしれない。しかし、知らなくて当たり前である。ダウンジングとは下の絵のような棒を持って水脈などの場所捜しをする迷信の中の迷信である。キング・オブ・迷信と言っても良いくらいのアイテムである。
 |
しかも、なんとダウジング&奇跡の水大好き人間が実は某新規材料開発部署の責任者だったりするので、そこらへんは考えると実はかなりコワイものがあるのだが、それはそれ、結構笑える事実(ホントにホント)ので良しということにしておきたい。
2001-03-04[n年前へ]
■柿ピーのシーソー・ゲーム 
柿とピーナツの供給バランスを考える
結婚しようとするカップルが少しばかり気にした方がよいのが、「柿ピーの好み」である。知らない人がいるとは思えないが、念のために書いておこう。柿ピーと言えば、柿ピー= 柿の種 + ピーナッツであって、亀田製菓の大ヒット商品である。そして、何と言ってもビールの安上がりのおつまみだ。
 |
この「安上がりで手軽なおつまみ」というところが、結婚しようとするカップルにはとても重要である。何故なら、結婚する前のカップルであれば洒落た店で飲むことも多いかもしれないが、結婚後はなかなかそうはいかない。いつの間にか手に持ったワイングラスは缶ビール(しかも発泡酒)に変〜身し、「テーブルの上の豪華な食事」はちゃぶ台の上の亀田製菓の柿ピーにバケラッタしているのである。
そうなると、かつては「このソースとても美味しいよね。うふっ。」なんて言っていた二人も変わらざるをえない。そりゃそうだ。柿ピーを目の前にして、気取ってみてもしょうがないわけだ。そんな時、こんな会話に走りがちである。
「柿の種ばっか、食べないでよ!」そう、柿ピーがなまじ「柿の種 + ピーナッツ」なので、片方がどんどん減っていったりすると、これがもう大変。かつては、ワインを片手に愛を語らっていた二人も、今やビール(しかも実は発泡酒)を片手に食い物の奪い合いをすることになるのである。
「オマエこそ、ピーナッツどんどん食えよ!」
これが、カップルの二人がとても似たもの同士で、「私達二人とも柿の種がスゴ〜ク好きだから、ピーナッツなんかいらないの。だから、- 柿の種だけが100%入った柿の種 - を買うの!」なんて感じなら、もちろんノープロブレムだろうし、あるいは、「ぼくらは、ピーナッツだけを買うのさ!」という感じのカップルでも同様だろう。
 |
あるいは、もう「ぼくは柿の種が好きだけど、きみはピーナッツが好き。二人は違っているから良い組み合わせなのさ。柿の種はぼくがどんどん食べるから、君はピーナッツをお食べ」なんてカップルでもいいだろう。こちらも、「ひとまずは」ノープロブレムである。つまりは、全く同じが正反対のカップルであれば、大抵の場合ほとんど問題はないのである。
しかし、「柿ピーは柿の種とピーナッツが適当な割合で入っているから良いのさ」なんていうグルメ気取りのカップルがいたりすると、大変である。
「アンタの食べる割合、少しおかしくない?」となるのは必至である。この数分後には、巨人の星の一徹父ちゃんのごとく、ちゃぶ台はひっくり返されているのに違いないのである。柿ピーの割合恐るべしだ。
「何言ってんだよ!オマエの方が柿ピー食べ過ぎだってんだよ!」
「そんなことないわよ!」
そして、しかもこれが理系カップルともなれば、もう最低だ。
「柿とピーの割合は7:3で食べなさいよ!」という具合になるに決まっているのだ。このままいくと、柿ピーを前にして離婚談義にもなりかねない。なんともオソロシイ話である。(* ピー柿は7:3でピーナツの方が多い。そんなのが実在することが私にとっては驚きである。)
「違うだろ、6:4が適正値に決まってるだろ!」
「そんなにピーナッツを食べたいなら、柿ピーじゃなくてピー柿*にしなさいよ!」
「別にピーナッツが過半数を超えるほどがイイって言ってんじゃねぇ〜!」
「何よ、もっと定量的に話しなさいよ!」
そういうわけで、「柿ピーの好み」「柿ピーの割合」「柿ピーの消費の割合」なんていうものは、結構結婚しようとするカップルには重要なのである。結婚しようとするカップルはぜひとも心して聞いておいてもらいたい。とはいえ、モテモテ度テストで
「女にモテない、というより、女に興味がないオマエ。今、一番気になることがドリキャスの値下げだったりなんかしない? まーそれも人生だけど、モテたほうがおいしいことは多いぜ? もうちょい女に関心持てよ。」と判定された私が言っても説得力がないか。
ところで、そもそも柿ピーの割合はどのくらいが普通なのだろうか?WEBで検索してみると、柿ピー10に対して
- 柿の種 : 7〜6
- ピーナッツ : 3〜4
そこで、試しに私も手元にあった小袋入り亀田の柿ピーの中身を調べてみた。調べたのは「小袋入り亀田の柿ピー」である。
 |
この一袋の中身を開けてみると大体こんな感じである。
 |
もちろん、単に数えても良いわけではあるが、「クダラナイことに、無意味なほどに大ゲサな道具を使うのがこのサイトのポリシー」でもあったりするので、まずは画像処理ソフトを使って柿の種とピーナッツの個数をカウントしてみた。使ったソフトはUTHSCSAImageTool である。PCベースでフリーでお手軽で粒子カウントとなるとこのソフトになるだろう。もちろんNIH-imageベースのScionImagePCという選択肢もないわけではないが、こと粒子カウントになるとはるかにImageToolの方が使いやすい。マクロの取っつきやすさ(機能は較べものにならないほどおちるが)もNIH-image系よりも上である。
さて、まずは上の画面内で柿の種を粒子カウントしてみたのが次の画面だ。この画面では見つかった柿の種は赤い縁取りがされ、個数がマーキングされていることがわかると思う。ちなみに、この画面内では93個の柿の種が見つかった。しつこいようだが、「数えた方が早いだろっ!」というツッコミはこの「できるかな?」では厳禁である。
 |
同じようにして、ピーナッツをカウントしてみたのが次の画面である。この画面では、ピーナッツは23個見つかった。
 |
すると、個数ベースでピーナッツが23/(93+23) = 20%で、残りが柿の種で80%ということになる。柿ピーの割合は大体8:2であったことになる。確か、WEBの亀田製菓に関する情報では
「柿ピー」のブレンドは、柿の種6に対してピーナッツ4が基本と書いてあったような気がするので、今回の8:2というデータは測定誤差、とその他の何らかの誤差が重なったものだろう。いや、そんな誤差はどうでも良いか。
ところで、大きな袋に入った柿ピーを食べながらよく考えることがある。私は柿の種が大好きなので、柿の種ばっかり選んで食べていくと、袋の口近くの上の方にはピーナッツばかりが残り、明らかに袋の場所ごとに柿の種とピーナッツの割合が異なってしまっていることがよくある。この柿の種とピーナッツの割合の時間的・空間的変化は一体どうなっているものだろうか?そこで、今回その「ピーナッツの柿ピーに占める割合の時間・空間的変化」について、少し考えてみることにした。
まずは簡単に判るように、袋の中から均等に柿の種とピーナッツを「柿ピーの割合を適当な割合で」食べていった場合、「ピーナッツの柿ピーに占める割合」は次の図のようになる。この図は横軸が時間で、縦軸がピーナッツの柿ピーに占める割合である。
緑 : 柿ピーを8:3の割合で食べた場合  |
今回の場合柿ピーは8:2で入っているので、青の場合のように柿ピーを8:2の割合で食べていくと、時間にして10分後に柿ピーがなくなるまで、ピーナッツの柿ピーに占める割合は20%をキープしたままである。しかし、(少しばかりピーナッツが好きな人が)柿ピーを8:3の割合で食べてしまうと、つまりピーナッツを過剰に食べてしまうと、どんどんピーナッツの割合は減ってしまい、ついに8分経過後にはピーナッツが袋の中から無くなってしまうのである。つまり、あとの2分は悲しみと共に柿の種を食べ続けなければならないのである(私は柿の種が好きなので悲しくもなんともないが)。
じゃぁ、袋の中の空間的分布も考えてみたらどうなるか、というのを次に計算してみた。まずは、袋を大きく二つに分けて、袋の入り口で適当な割合で柿ピーを食べた後、袋の奥から袋の入り口の方へ柿ピーを持ってくる。また、その際に適度に柿ピーをかき混ぜる。そして、柿ピーがなくなるまで柿ピーの割合の変化を調べてみるのである。ちなみに、IE4以降+Excel2000以降?の人であれば、ここをクリックすれば、その計算シートで遊ぶことができると思う。
例えば、「柿ピーを8:2の割合で食べた場合」と「柿ピーを8:5の割合で食べた場合」のピーナッツの柿ピーに占める割合の時間・空間的変化を調べてみたのが、次に示す結果である。ちなみに、このいずれも横軸は時間である。また、時間軸にして30前後の時点で柿ピーは完全になくなっている。
 ちょっと計算上の誤差が大きいが、それはちょっと無視してもらいたい。 |
さて、左の「柿ピーを8:2の割合で食べた場合」、つまり本来の柿ピー比と同じ割合で食べていった場合には、入り口近くでも奥の方でも柿ピーの比率は変わらない。そして、入り口の方から柿ピーを取った分を、奥の方から補給しているので、奥の方では時間軸20の時点で空になってしまっている。左の図でピーナツの割合がゼロになっているように見えるのは、実は単に柿ピーがなくなっただけなのである。そして、入り口近くの柿ピーが時間軸30の時点で空になっているまで、柿ピーの比率は変わることはない。当たり前だ。
では、「柿ピーを8:5の割合で食べた場合」はどうだろうか?つまり、本来の割合よりもピーナッツを多く食べがちな人の場合だ。そんな場合の右を見てみると、奥の方は単に入り口近くに柿ピーを補給しているだけなので、柿ピーの割合は変わらないままだ。しかし、入り口近くではあっという間にピーナッツの割合が減ってしまっている。ほとんどなくなっている、といっても良いくらいの状態である。つまり、ピーナッツ大好き人間にとっては、手の届く袋の入り口近くには全然ピーナッツがないという、拷問状態なのである。周りに女子校や共学の学校はあるけど、自分の通う学校が男子校だったみたいなキツイ状態である。ちなみに、私は高校時代に私服の共学の学校に通った結果、制服の女子高生に強い強い憧れを抱くに至ったことを否定できなかったりするのである。
話を戻して、それでは「袋を適当にかき混ぜながら」、「柿ピーを8:5の割合で食べた場合」はどうなるだろうか?というのが次の結果である。こうすると、奥の方のピーナッツもどんどん消費されているのがわかる。入り口近くも奥の方も、同じようにどんどんピーナッツの割合がどんどん減ってしまい、時間軸15の時点で完全になくなってしまっている。あとは柿の種がなくなる時間軸30の時点まではもう柿の種と向かい合うだけの人生なのである。ツラすぎる(ピーナッツ好きの人にとっては)。私の知人のオッパイ星人が結婚後に妻から、
*一部、不適当な発言がありましたことをお詫びします。
 |
つまりは、ピーナッツが食べたいからといって、あまり柿ピーの袋をかき混ぜるのは良くないということなのである。もちろん、短期的にはピーナッツがたくさん食べることができて良いわけであるが、長期的に見ればその後の長い「柿の種人生」が待っているのである。それが端的にわかるのが、次の「ピーナッツをどれだけ食べているか」を示す結果である。
この結果の中で、上の方に示した「柿ピーの袋をかき混ぜない場合」では、結構最後までピーナッツを細々と食べていけることがわかるだろう。柿ピーがなくなるのが時間軸で30前後の時点であるが、その少し前23位の時点までピーナッツを食べていけるのである。それに対して、ピーナッツを早く食べたいばかりに、柿ピーの袋をかき混ぜまくりの下の「柿ピーの袋をかき混ぜた場合」には、時間軸で13前後の時点でもうピーナッツがなくなってしまっている。もう、コイツには「柿の種人生」しか残されていないのである。
| 柿ピーの袋をかき混ぜない場合
結構最後までピーナッツを細々と食べていける |
| 柿ピーの袋をかき混ぜた場合
なんとも、太く短くのピーナッツの食べ方である… |
とはいえ、柿ピーの袋をかき混ぜながら太く短くピーナッツを食べるか、それをじっとガマンの子で細々と最後までピーナッツを食べるか、どっちが良いかは難しいところだ。ちなみに、私はかき混ぜまくりで柿の種を食いまくり、残ったピーナッツは人にプレゼントするというとても良い性格である。だったら、100%柿の種を買えって感じであるが、売店には置いてないことも多いから、しょうがないのである。
というわけで、今回はビール(やっぱりあくまで発泡酒)を左手にそして柿ピーを右手でつまみながら、酔っぱらった頭で(いつものことだが)、ツマラナイことを考えてみた。モノが本当の柿の種であればオチて芽が出るのが普通なのだけれど、今回の柿ピーの話はオチがあるわけでも芽が出るわけでもない。酔っぱらいのタワゴトだから意味なんか全然ないのである。と、日記には書いておこう(意味不明)。
2001-04-07[n年前へ]
■スカートの力学 予習編 
風に吹かれるスカートは
四月になって、春風が強く吹き始めた。春風と言えば聞こえは良いけれど、コンタクトレンズを使っていたりする人は強い風が吹くとゴミが入ったりしやすくて辛いだろうし、まして花粉症だったりすると涙が止まらなかったりしてきっと辛いことだろう。そんな辛い季節でも、たまにドキドキするような気持ちになる瞬間がある。もちろん、それは春風にスカートが舞い上がった瞬間だ。スカートが風に吹かれた瞬間に、私は理由もなく(いや理由はちゃんとあるのだが)心と体がドキドキする。それはもちろん私だけでなくて、男なら間違いなく誰しもがそんなドキドキを味わったことがあるはずだ。もっとも、そんな男心を理解しないヤカラはそんなドキドキを軽蔑するに違いないのだが、それが男というものなのだからしょうがないのである。
とはいえ、男心は「男の心」という位だから、女性にはなかなか判りづらいことだろう。「女子高生なんかはどうせスカートの下に短パンを履いているのに、それでもドキドキするものなの?」などと言う女性も多い。しかし、「それでもドキドキしたりする」ものなのである。いや、もちろんスカートの下にジャージを履いてるなんてもっての他ではあるが、短パンくらいならドキドキ度は全然減らないものなのである。それが、つまりは男というものなのだ。
そして、逆に「スクール水着の秘密」ではないが、女性には常識でも我々男には全然判らないことが世の中にはたくさんあるに違いない。ちなみに、私にとってはスカートもその一つである。何しろ、あまりスカートについて自分のこととして考える機会がなかったのである。いや、実際のところそんな機会は全然無かったのである。そこで、今回は「春風に吹かれるスカート」について考えてみることにした。(本題に入る前に一応書いて置くけれど、今回も「スクール水着の秘密」と同じく、女性から見たら「なんて当たり前のことを」とか「それちょっと違うんじゃないの」ということを書いている。そんな風に感じた方は是非、メールででも私に情報でも頂けたら、と思う次第である。)
| さて、本題である。 この右の図のような「風に吹かれながら女性がスカートを押さえている風景」をよく見かける。もっとも、「よく」見かけるなんていうと、私がさぞそういう風景を探し求めているように聞こえるかもしれないが、そんなことはない。風が強い季節であれば、そんな風景は満ちあふれているのである。 さて、この女性のスカートのように風に吹かれたスカートについてちょっと考えてみよう。
| 女性がスカートを押さえている風景」 (animeBODY)  |
まずは、体の前方から強い風が吹いているものとする。つまり、強い向かい風が吹いている状態である。ちょっとその女性にとってはツライ状態である。そこで、うすみどり色のスカートを履いている女性は、スカートがめくれ上がらないように、スカートの前部を両手で膝近くで押さえているわけだ。しかし、それでも風に吹かれてスカートの後ろは舞い上がってしまう。例えば、下の右図で女子高生の体の後ろでスカートがめくれ上がっている。それをもっと単純にしたのが左で、この図中ではスカートはCの位置まで上がってしまっている。
 |  M.H.Tさん画 |
もちろん、男心からすればCどころではなくて、Aくらいまでスカートには高く高く舞い上がって欲しいわけであるが、女心からすればそれはとんでもない話だろう。
さて、このスカートのめくれあがる位置Cは何で決まるだろうか?もちろん、流体力学・弾塑性体力学などを総動員して解かなければならないわけではあるが、それは次回以降のお楽しみということにしておいて、予習編の今回は単純にスカートがOC方向には曲がらないものとしてみよう。だとしたら、話は簡単だ。ただスカートの裾の広さでCBの長さは制限されるわけである。スカートの裾が広ければ、スカートの端は高くまでめくれあがってしまうし、スカートの裾が狭くなっていれば、スカートは比較的低いところまでしかめくれない。
だから、この下の色々なスカートの中でプリーツ・スカートのようなフレアタイプの場合は、スカートは高隈でめくれ上がってしまうだろうし、タイトスカートのようなスカートの裾が狭いものであれば、強い風にも負けず、スカートはめくれ上がることはないだろう。
プリーツ・スカート
|
|
|
|
しかし、しかしである、スカートの裾を狭くすれば春風にスカートが舞い上がってしまうことはなくなるかもしれない。だけど、スカートの裾の長さが制限するのはスカート自身だけでない。スカートを履いている女性の動き自体も制限してしまうのである。それではずいぶんと窮屈になってしまうことだろう。スカートの裾が狭いせいで歩幅も狭くなって、走り回ったりすることもできなくなるに違いない。だからこそ、脚を蹴り上げる藤原紀香のJ-PHONECMのスカートも、脚の動きが制限されないように、スカートの後ろに切れ目が入っているのだろう。
ということは自由に駆け回ったりしようとすると、つまり、スカートが足枷にならないような裾の広いスカートを履いていると、そんなスカートは風に吹かれて舞い上がりやすいわけだ。そして、そんなスカートを履いていると春風に困らせられることになる。
とはいえ、実際にスカートを履いたことがあるわけじゃないから、私には実際のところよく判らない。だから、女性の方々の「本当はこうなのだ」という教えでも請うしかないのである。結局、スカートの話は、スカートを履く人には常識きわまりない話だろうが、私はこれまで考えたこともなかったので全然よくわからない。これが、男と女の常識の違いなのかもしれない。いや、単に私の常識知らず、という可能性が一番大ではあるのだけれど…
そういえば、辞書でskirtを引いてみると「女;女の子」なんていう風にも書いてあった。なるほど、風に吹かれるスカートも走り回るスカートも、確かにその女性そのものなのかもしれないなぁ、と少しばかり思ったりしたのである。だとしたら、風に吹かれるスカートは向かい風には負けないで欲しいな、と柄にもなく思ってみたりするのである。ホントに私の柄じゃないのだけれど。





