1999-02-28[n年前へ]
■分数階微分の謎 
線形代数、分数階微分、シュレディンガー方程式の三題話
分数階微分?
InterLabの1999No.5を読んでいると面白い記事があった。いわき明星大学理工学部の榊原教授の「Waveletと数式処理ツール」という記事である。といっても、興味を持ったのはWaveletのことではない。もちろん、Waveletに興味がないわけではない。この榊原教授が講師を務めたWavelet講習にも参加したこともある。しかし、今回興味を惹かれたのはその記事中にあった「分数階微分の解析」である。InterLabの榊原教授の記事を引用すると、-通常微分・積分は整数回実行できるが、分数階微分はこれを分数に一般化したものである。さまざまな物理や工学の現象の記述に使われるようになった-とある。一階微分とか二階微分というものはよく使うが、0.5階微分などというものは使ったことがない。どのようなモノなのかさえよくわからない。
参考:
一体、どんな物理や工学の現象の記述に使われているのか知りたくなったので、infoseekで調べてみる。すると、いわき明星大学の清水・榊原研究室の「粘弾性動モデル」が引っ掛かる。
参考:
衝撃吸収・シリコーンの弾性率などに興味を持っている人には面白いかもしれない。もう少し調べてみると「バナッハ空間バナッハスケールにおける分数階積分作用素」というようなキーワードも引っ掛かる。
そこで、まずは勝手に分数階微分について考えてみた。
分数階微分・積分の勝手な想像図
まずは、イメージを考えるためにグラフを作成してみる。x^2の関数、および、それを微分・積分した関数である。微分は3階まで、積分は2階まで行っている。
 |
このグラフ形式の表示をちょっとだけ変えてみる。
 |
ここまでくると、平面グラフにしてみたくなる。つまり、微分・積分の階数を離散的な整数値でなく、連続的な値としてのイメージに変えたくなる。
 |
これで、微分・積分が整数階でない場合のイメージ(勝手な)ができた。微分・積分が離散的なものではなくスムーズにつながっているものであるというイメージである。図.2から図.3への変化をよく覚えていてほしい。
といっても、これは数学的なイメージのみで物理的なイメージはまだここでは持っていない。位置、速度、加速度などの微分・積分で選られるものに対して同じようなイメージを適用すると、位置なんだけれどちょっと加速度っぽいもの、とか、速度と加速度の「合いの子」みたいなものというような感じだろうか?
さらに、これから先は、f(x)という関数が示す無限個の値を位置ベクトルと考えて、f(x)というのは無限次元空間の一つの点だというイメージを持つことにする。線形代数を考えるならそれが一番わかりやすいだろう。任意の階で微分された関数群が集まって、さらに高次元の空間をなしているというイメージである。
分数階微分を調べる
勝手なイメージはここまでにして、手元にある数学の参考書の中から手がかりを探してみた。すると、大学院入試問題解説 - 理学・工学への数学の応用 - 梶原壌二 現代数学社ISBN4-7687-0190-6
の中に手がかりがあった。あれ、ということは以前にやったはずなのか...そう言えばおぼろげな記憶がちょっと...
その中の言葉を少し引くと、
フーリエ変換は等距離作用素である、関数空間L^2(R)における回転といえる。結局、
となる。そして、古典力学におけるハミルトン関数において、運動量を微分演算子で置き換えれば、量子力学や量子化学のハミルトン演算子が得られ、シュレディンガー方程式などにつながるのである、とある。他の資料を眺めてみると、どうやら量子力学などの分野からの要請に応じてここらへんの微分演算子の分野が発展しているようだ。理論物理などをやった方ならよくご存知のことだろう。例えば、水素原子の基底状態の波動関数へ運動エネルギーの演算子を作用させるというような、基本的な所でも、このフーリエ変換を用いた微分演算が用いられてる。ここで、fは元の関数であり、Fはフーリエ変換
さて、この式自体は非常に簡単である。それにイメージも湧きやすい。
i を掛ける演算、私のイメージでは複素数空間の中で90度回転をする(言い換えれば、位相が90度ずれる)演算、が微分・積分であるというイメージはスムーズに受け入れやすい(それが正しいかどうかは知らないが)。なぜなら、微分が空間の中での回転であるとすると、三角関数の微分・積分に関する性質(例えば、Sinを微分するとCosに、Sinを2階微分すると-Sinになる、すなわち、一回の微分につき位相が90°ずつ回転する(位相がずれる)というような性質)が納得でき、それがフーリエ変換という形で登場してくることがスムーズに受け入れられるのである。また、微分といえばとりあえず三角関数の登場というイメージもある。
もう少しわかりやすく書くと、
- 三角関数では一階微分の結果は90度位相がずれる(回転する)。
- ならば、(例えば)0.5階微分は45度位相をずらせば良い。
- 任意の関数もフーリエ変換により、三角関数に分解される。
- ならば、任意の関数に任意の実数値の微分が成立する。
任意の関数をフーリエ変換し三角関数に分解した時の位相、言い換えれば、周波数領域での位相ずらし、で分数階微分が定義されるということは、物理的実用的に大きな意味を持つ。例えば、電磁波、弾塑性運動などの物理現象の中での位相変化を分数階微分で解けることになる。例えば、複素貯蔵弾性率などについて分数階微分との関係は深そうである。あるいは、媒体中の電磁波の位相などについて適用するのも面白そうである。
分数階微分を使ってみる
よく分からないところも多いが、とりあえず、
という式を使ってみる。まずは、使ってみないとわからない。とりあえず、1次元の関数を作成して、この式を適用してみる。まずは、よく出てくるガウス分布で適用してみる。まずはガウス分布とそれの通常の一階微分の解析解を求める。
 |  |
それでは、今回の方法による一階微分の結果と、それと解析解との比較を示す。なお、本来無限領域のフーリエ変換を有限の領域で行っているため、端部近くで変なことが生じるのはしかたがないだろう。また、色々な事情により係数の違いは無視して欲しい。
 |  |
ちょっとずれが生じているが、こんなものだろう。しかし、これだけでは今回のフーリエ変換を用いた微分の面白さはでてこないので、0から2の範囲で連続的に分数階微分をしてみる。
 1/10 (=0.1)階微分 |  1/2 (=0.5)階微分 |  7/10 (=0.7)階微分 |  1階微分 |
 13/10 (=1.3)階微分 |  15/10 (=1.5)階微分 |  17/10 (=1.7)階微分 |  2階微分 |
モーフィングのようで面白い。
さて、今回は分数階微分を勉強してみる所までで、これの応用は別に行ってみたい。もちろん、言うまでもないと思うが、間違いは多々あると思う。いや、田舎に住んでいるもので資料がないんですよ。
2000-02-19[n年前へ]
■携帯電話の同時性? 
競馬の写真判定とパノラマ写真 その後
先日
を書いてから面白いメールを頂いた。その一部を抜粋すると、小生は超音波を利用した新しい流体場測定を行っていますが、この方法で得られるDataは空間1次元時間1次元の2次元データです。従って得られるのは、このページにあったような画像が直接得られるわけです。とある。この方法といくつかの結果を発表してから、あちこちからコンタクトがありましたが、その中の一つが、NYのSirovichという高名な流体力学者からの手紙でした。彼はいわゆるSnapShotを、逆に小生のデータから構築できないか、というのです。
今このWebでされたことの逆をしたいというわけです。流れの空間構造を解析するために使いたいのです。残念ながらこれは、以下に少々説明するように、原理的に無理な話で断らざるをえませんでした。
つまり、時間軸に速度をかけて空間軸に変換できればよいのですが、流体場はそれ自身が速度分布を持っていますから、一体何を使えば良いのかが定まらない。
電磁波の場合には光速が一定ですから、時間情報から空間情報を得ることができますが、古典流体力学では不可能なのです。工学的には平均流速を使って、時間-空間の変換をしますが、それはインチキとまでは言わないまでも、便宜的なも
のでしかありません。このWEBの中での例では、馬?の速度のみであとは静止しているので、可能でし
ょう。
「馬?」という箇所に、私との意見の相違があるようだ。私が明らかに「馬」であると言い張っているものに疑問を持たれているような気がするのであるが、今回そこは気にしないでおく。
なるほど、音波や電磁波などを使って計測を行い、得られた
- 空間(あるいは量)-時間
- 空間(あるいは量)-空間
- 海の中の魚を探知する「魚群探知機」
- 気象状況を計測する「気象レーダー」
- 固体の中の電荷分布を計測する「電荷分布測定装置」
「魚群探知機」は超音波を水中に発信して、その反射波が刻々と帰ってくる様子から、(超音波の速度を用いて、空間位置に変換した後に)障害物(ここでは魚群)の様子を計測するものである。「気象レーダー」も電波を使って同様に雲の分布などを測定する。
「電荷分布測定装置」の場合は、(例えば外部電界を印加し)電荷を持つ個所を振動させてやり、その振動がセンサー部に刻々と伝わってくる様子から(あぁ、なんて大雑把な説明なんだ)、(固体中の弾性波の速度を用いて、空間位置に変換した後に)固体の中にどのように電荷分布が存在しているかを計測するものである。
と、文章だけでは何なので、WEB上から、それらの計測器を用いた場合の計測例を示してみる。
下が魚群探知機である。リンク先は
である。 |
また、この下は空間電荷測定装置である。これなども、とても面白いものだ。リンク先は
である。 |
さて、こういうことを、調べてみるだけではしょうがない。自分でもそういう計測をしてみたい。
そこで、次のような実験をしてみようとした。
- 部屋の中に複数の「音の発信源」を配置する。
- 複数の「音の発信源」から同時に音を発する。
- それをPCで収録する。
- 音声が「音の発信源」からPCに到達するまでの時間を解析する
- 複数の「音の発信源」の位置を計測する。
そこで、安易にも時報を使おうかと考えてしまった。しかも、数があって手軽ということで、携帯電話を使おうとしたのである。
しかし、複数の携帯電話を集めて、117に電話して時報を同時に聞いてみると、とても同時どころではない。てんでばらばらなのである。電話のスピーカーから流れてくる時報のタイミングには結構ズレがあるのである。
携帯電話の間には結構同時性がないのだ。また、固定電話とも比較したが、固定電話よりも時報が速いものもあれば、遅いものもあった。
そこで、複数の携帯電話を聞き比べた結果を以下に示してみたい。この写真中で左の携帯電話ほど時報が先に流れており、右になるほど時報が遅れているのである。一番早い左と、一番遅い右では一秒弱の違いがあった。
 |
また、参考までに、家の固定電話と携帯電話の時報を一緒に聞いたサウンドファイルを示しておく。
この携帯電話は先に示した画像の一番左である。つまり、先の携帯電話群では一番時報が早かったものなのである。しかし、家の電話よりは一秒弱遅かった。ということは、家の固定電話と先の一番遅い携帯電話では時報の時間にして2秒弱の違いがあることになる。 そして、「家の固定電話と携帯電話の時報を一緒に聞いた音の変化」をスペクトログラムにしたものを以下に示す。
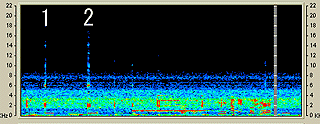 |
水平軸が時間軸であり、時間は左から右へ流れている。また、縦軸は音の周波数を示している。ここでは、「1」で示したのが家の固定電話の時報であり、少し遅れて「2」の携帯電話の時報が聞こえているのが見てとれる。
よく時報を確認することはあるが(実は私はほとんどないのだが...)、携帯電話・PHSで時報を聞く限り、秒の精度はそれほどないようである。また、勤務先の固定電話は先の携帯電話群と比べても遅い方であった。それは少し意外な結果であった。
今回調べた「携帯電話の同時性のなさは」は常識なのかもしれないが、電話の時報で時計を合わせるのはあまり精度が出ないやり方であることがわかっただけでもよしとしよう(別に実験を途中で投げ出した言い訳ではないけれど)。
今度、TV(衛星TVなども遅延時間を考慮した時報の放送を行っていると聞くし)やラジオを用いて当初計画していた実験を行おうと思う。その際には、時報がPCに到達する時間のズレで「音の発信源」までの距離を計測し、左右のマイクでの違いを計測することにより、「立体音感シリーズ」のように「音の方向」を得てみたい。
というわけで、話が「立体音感シリーズ」に繋がったところで、今回は終わりにしようと思う。
2000-05-12[n年前へ]
■メガネの内側にある歪み 
隠れたストレスに光を当てろ
また、可視化の話である。いや、自分でも忘れていたが、「可視化」改め「見える?見えない?」シリーズである。今回はメガネの内側にある「歪み」、隠れたストレスに光を当ててみたい。そして、そこに何があるかを見てみたいのである。
私の眼はどうも明るさに弱い。やたら太陽の光が眩しく感じることが多い。といっても、単に私のガマンが足りないだけかもしれない。あるいは、睡眠不足のせいかもしれない。そして、私は同時に暗さにも弱いのだが、こちらは単にビタミン不足による鳥目だろう。
そういうわけで、明るいのに弱いので車を運転する時には大抵サングラスをかけている。サングラスは何本も持っているわけだが、最近のお気に入りはこれである。
 |
これは、偏光フィルター機能付のサングラスである。偏光というギミック付のところがお気に入りの理由である。以前、
で書いたように、偏光フィルターがあれば色々なものの反射光のみを遮ったりすることができる。例えば、下の右側の写真では左の写真に比べてガラス表面の反射光が減少していることがわかるだろう。これは偏光フィルターの作用のせいである。 |  |
これと同じように、偏光フィルター機能付のサングラスを使えば色々な反射光を防ぐことができる。例えば、通常は反射光などで車のフロントグラスの内側にいる人の姿はよく見ることができない。しかし、このメガネをかけていれば、反射光に邪魔されずフロントグラスの内側を見通すことができるのである。もう、対向車なんてまるでフロントグラスがないかのようである。
この偏光フィルター機能付のサングラスは、通常「釣り」などで用いられるものだ。水面の反射光を防ぐことにより、水中の魚の姿などを見やすくするためのものである。結構、海の近くに住んでいる私にはうれしい機能である。
このサングラスをかけている時に、ふとある実験を思いついた。普段は透明にしか見えない「普通のメガネ」の影に隠れたストレスを目に見える形にしてみようと思ったのである。よく、「メガネの奥にストレスが隠れている」というが、そのストレスを見て取れる形にしようと思うわけだ。
そこで、新婚ホヤホヤの「夜の帝王」I田氏(関係ないが、I田氏から「Hirabayashiさん、小杉のメーリングリストで-できるかな?-の話題が出てましたよ。」と言われた時はビックリした。とりあえず、どなたか知らないが、メーリングリストで紹介して頂いた武蔵小杉勤務の方には一言お礼を言っておきたい)にメガネを借りてみた。このメガネをじっくり眺めてみてもらいたい。
 |
この透明なメガネの奥に何か見えるだろうか?そこに「歪み」は見えないだろうか?「透明だから、何も見えないだろう。」という人もいるだろうが、あるグッズを使うと、もう明らかに見えてくるのである。それが、下の写真である。レンズを固定している辺りをよく見てもらいたい。不思議な
虹模様と十字の模様が見えるはずだ。
 |
プラスチック等は製造過程での不均一な応力や、外力により複屈折性を示す。光弾性と呼ばれる現象である。そのため、偏光面を直行させた偏光フィルターの間にそういうプラスチックなどを挟みこむと、その弾性体の内部に働いている応力分布の状態を調べることができる。それを応用したのが、偏光顕微鏡などである。
例えば、下の写真はカセットテープのケースの左側部分を、偏光面を直交させた二枚の偏光フィルターで挟んでみたものである。見事に弾性体の内部に働いている応力分布が可視化できているのがわかると思う。これを応用すれば、例えば熱変形をしているようなものであれば、透明体の熱分布も簡易的に見て取ることができる。
 |
そういうわけで、先の写真あるいはそれを拡大した次の写真のように普通では見えない透明なプラスチックレンズの中に隠れている「ストレス」を見て取ることができるわけだ。
 |  |
とりとめもないが、今回は透明なメガネの影に隠れたストレスに光を当ててみた。ちゃんと見ようと思いさえすれば、目に見えるものは数多くある。「見える?見えない?」の境界線はその人自身が決めるのである。「できるかな?」では、これからも色々な「見える?見えない?」を追求し、「見えるかな?」について考えていきたいと思う。
2000-07-02[n年前へ]
■続 オッパイ星人の力学 
揺れる胸の動き編
前回、「オッパイに関する力学的なつり合い」を考えてみた。そして、
- 「バストに関するフックの法則」
- 「バストに関するヤング率」
さて、前回登場した私の友人のオッパイ星人ではないが、「通り過ぎる女性の胸をに目を奪われる人々」は多い。街中を歩いているオッパイ星人達を見分けるのは簡単である。視線が妙に上下・左右に揺れ動くヤツを見つければ良いのである。しかも、何人ものオッパイ星人達がそろいも揃って全く同じ目の動きをしているから、すぐ判るのである。もし、オッパイ星人達が地球征服を企みはじめた場合には、オッパイ星人達の目の動きにより地球人と区別する方法を私は提案してみたい。
しかし、「視線が妙に上下・左右に揺れ動くヤツ」といっても、それがどのような動きなのか知らないことには困ってしまう。もしかしたら、単に落ち着きのない一般人かもしれない。無実の人間にオッパイ星人疑惑をかけるわけにはいかない。オッパイ星人達の目がロックインしているバストの動きを知らないことには、オッパイ星人達の企む地球征服を阻止することはできない。
そこで、「私は正義、そして地球防衛のために」、歩いている最中の「バストに関する動力学」を考えてみることにした。歩いている最中の「バストの動き」を研究することにより、オッパイ星人の識別、ひいてはこの地球を守りたいと切に願う次第である。この私の目的をくれぐれも忘れないで頂きたい。
まず最初に、歩いている時の人の胸板の動きを考えてみることにしよう。一秒間の間に、
- 左足で一歩 -> 右足で一歩
 |
当然、この動きを見て違和感を感じる人がいるだろう。人は歩くときに、足先を円の中心にして進んでいくのだから、次の図のようにSin関数の絶対値をとったような形状になるのではないか、という考え方である。
 |
しかし、私は二つの理由により、この一見自然らしく思える「人の胸板の上下の動き」を採用しないことにした。
まず第一に、人間の足、胴体にはクッションのような働きがあり、この形状のように鋭い変化はしない、としたいのである。実際、街中を歩く人々を観察した結果でも先に示したような「人の胸板の上下の動き」であった。
第二に、この一見自然らしく思える「人の胸板の上下の動き」だと計算が面倒なのである。これでは私が困ってしまう。
というわけで、二つも問題がある考え方を採用するわけにはいかず先に示した人の胸板の上下の動きを用いることにした。
そして、その時の「人の胸板の左右の動き」を示すと次のようになる。
 |
さらに、この胸板の軌跡を女性の前方から眺めると次のようになる。想像力が豊かなオッパイ星人であれば、もうこの図に視線が釘付けのハズである。これが、上下左右に動くバストの土台としての胸板である。
 |
これはまるで指揮者が振るタクト、指揮棒のようである。この胸の土台が振るタクトに合わせて、我らがバストは揺れ動くわけだ。それでは、このように「胸板」が動くとした時に、
- 「バストに関するフックの法則」
- 「バストに関するヤング率」
 |
これが揺れるバストの動きのプロットである。ということは、これがオッパイ星人が揺れるバストに視線をロックインしているときの視線の動きでもある。そう、忘れているかもしれないが、「私は正義、そして地球防衛のために」、「オッパイ星人」を見分けるためにこの研究をしているのである。
そして、これが走っている状態ともなれば、こんな感じだ。これは1秒で6歩であるから、かなり速く走っている状態に揺れ動くバストの軌跡である。そう、あなたもよく街中で見かけたことがあるはずのあのバストである。この小気味良いリズムはどうだろうか。
 |
このグラフを見ても、なんてつまらないグラフだと思う人もいるかもしれない。そういうアナタは安心して大丈夫である。確かにあなたは普通の人間である。しかし、「この小刻みに揺れる動き」に美を感じる人がいたならば、あなたは少しヤバイ状態である。そうオッパイ星人の可能性がある。
そして、もしあなたが街中で視線をこんな感じで小刻みに揺らすヤツを見かけたら、そやつは人間ではない。オッパイ星人のはずである。要注意だ。私と一緒に正義・地球防衛のために戦って欲しい。
ただひとつ心配事があるとしたら、この研究をしているうちに「正義の味方であるこの私」の感受性が豊かになってしまったことである。妙にこのグラフに美を感じ始めているのである。そして、妙に文章に気持ちがこもっているような気がしてきたのである。いや、まさかとは思うが...
ところで、今回の計算はバストの動きが「バストに関するフックの法則」で決まるものとしている。つまり、バストを胸板に拘束する力がバストの弾性だけという状態である。簡単に言えば、全てノーブラ状態で計算を行っている。パラダイスである。いや、むろん私にとってではなくて、オッパイ星人にとってである。
オッパイ星人の力学はまだ始まったばかりだ。正義・地球防衛のために、私は研究を続けるのである。
2000-08-13[n年前へ]
■WEBの時間、サイトの寿命 
ゆっくり長く続けましょうか?
以前、
でロゲルギストが- 第五物理の散歩道 ロゲルギスト著 岩波新書 「通信を考える」
- その系の情報処理の単位時間
- その系の信号の伝わる速度
- その系の空間スケール
- 空間スケール < 情報処理の単位時間 × 信号の伝わる速度
- 大人数から構成される企業のスピードは、少人数から構成される企業のそれには遙かに及ばない
ところで、ロゲルギスト達はある系の「単位時間・信号伝達速度・大きさ」の間の関係について、
- 「単位時間・信号伝達速度」を入力値として、「大きさ」を考える
- 「大きさ・信号伝達速度」を入力値として、「単位時間」を考える
さて、寺田寅彦が「単位時間・信号伝達速度・大きさ」について、さらにどのようなことを展開していたかというと、それはある系の「大きさ・寿命」についての関係である。寺田寅彦は
- 空想日録 三 身長と寿命 (寺田寅彦随筆集 第四巻 岩波文庫 小宮豊隆編)
- 人体感覚について振動感覚の限界を調べた実験データ、 - 人は自らの体の固有振動周波数の振動に対してもっとも過敏である- 、というものをきっかけとして、
- 生物の時間の長さの単位は相対的なものである
- ある系の「時間の長さの感覚 = 相対的な単位」はその系の固有周期と密接な関係がある(振り子時計なんてわかりやすいだろう)
- ある系の「寿命」を測る単位は、その系の「時間の相対的な単位」、すなわち、その系の固有周期だと想像してみよう。
- その場合、ある系の固有周期はその系の大きさに比例するから、大きい動物ほどその系の「時間の相対的な単位」は長いものとなり、見かけ上の「寿命」はその動物の「大きさ」に比例するだろう。
なるほど、サイズが小さい動物(すなわち固有振動の波長の短い動物)にとっては、ほんの小さな変化も大きな変化である。ということは、その動物の感じる「時間単位」は短くなければ、生き残れないだろう。逆に、サイズの大きな動物は俊敏な動きはできないわけで、その動物の「時間単位」は長くならざるをえないだろう。
ゾウのような大きい動物は「時間単位」が長く、一見「寿命」が長いように見え、ノミのような小さな動物は「時間単位」が短く、一見「寿命」が短く見えるというわけだ。実は、ゾウもノミもその動物自身の「時間単位」を基準にすると、同じ寿命を生き抜いているということになる。
本川達雄の中公新書「ゾウの時間 ネズミの時間」では- 体重の4分の1乗に比例して「その動物の時間単位=生理的時間」が長くなる-と述べられているが、昭和八年に既に寺田寅彦は体重は身長の3乗に比例する、逆に言えば体重は身長の3分の1乗に比例するから、「体重の3分の1乗に比例して時間が長くなるだろう」と想像を巡らせているのである。素晴らしい、想像力である。
さて、寺田寅彦はロゲルギストと違って、「単位時間・大きさ」については言及しているが「信号伝達速度」については触れていない(その替わり、さらに「寿命」にまで触れているわけであるが)。もっとも、私があえて書き加えてみるならば、ある系の固有振動にはその系の中での弾性が密接に関係するし、弾性はその中での弾性波の速度も密接に関係する。つまり、ある系の固有振動の周期というものには「その系中での波の伝達速度」が暗に隠されていて、寺田寅彦は単にそれを一定とおいていたわけで、寺田寅彦が述べた内容は実はロゲルギスト達の述べた内容を包括している、と私は思うのである。
このような「単位時間・大きさ・信号伝達速度・寿命」に関する話は動物に限るものではない。
- ロゲルギストが「信号伝達速度=光速度」として、「処理速度を確保する」ための人類の行動範囲について論じたり、
- 私(いきなり自分を例に出すのも何だが)が「信号伝達速度の変化」と「大きさ(人口)の変化」から人類の処理速度の変化について論じたり
さて、前振りが長くなった。前回、
では、単に「信号伝達速度の変化」と「大きさ(人口)の変化」を並べて「処理速度」の変化について考えてみただけだった。今回は寺田寅彦が考えたのと同じく、「信号伝達速度」と「大きさ(人口)」から「寿命」が決まると考えることにより、「人類」の「寿命」の変化について考えてみることにしたいと思う まずは、前回使った「人類の大きさ=人口」の変化が次のグラフである。ただし、この人口は全然正確ではないし、むしろかなり不正確なものであることは先に断っておく。ここでは、細かな値を使うのが目的ではないので別に構わないだろう。
 |
そして、「人類」の中での「情報伝達速度」の変化を示したものが次のグラフである。この速度が「人類」という集合体の中での波の進行速度を決めるのである。
 |
それでは、「人類」という集合体の固有振動はどうやって扱うかというと、この
- 「人類の大きさ=人口」
- 「情報伝達速度」
- 人口 / 情報伝達の速度
その、人口 / 情報伝達の速度 = 「人類の固有時間」を計算してみたものを次に示してみよう。
 |
こうしてみると、人類というヒトの集合体においては、どんどん時間の流れは速くなり、それに応じて見かけの「寿命」は短くなっている、ということがわかる。人類はまさに生き急いでいるのである。もし、この流れを止めようと思ったら、どうしたら良いだろうか?それには、今回の計算から言えば情報転送速度を遅くするか、人類の大きさを大きくするしかない。情報転送速度を遅くするのはなんとも後ろ向き(byわきめも)だし、人口を減らすというのもなんとも後ろ向きだ。だとしたら、宇宙へでも人類が進出して、人類の空間的なスケールを大きくしていくしかないのだろうか?これもまた難しい話である。
さて、最近、大好きなWEBサイトが閉鎖してしまったり、更新速度が遅くなっていたりしていて少しさみしい。だけど、もしかしたら各WEBサイトにも、「更新速度が速いと、WEBサイトの寿命が短い」なんて法則が実はあるのかもしれない。更新速度が速いということは、そのWEBサイトの固有時間が速く流れているということで、限られた寿命をどんどん使い果たしているのかもしれない。
だとしたら、更新速度が遅いということはそのWEBサイトの寿命が長くなるということだから、それはそれで良いのかなぁ、などと思ってみたりする。「太くて短い寿命」も「細くて長い寿命」も実は本人からすればどちらも同じ長さなのかもしれないけれど、外から見ている私は「細くても良いから長く続いて欲しいなぁ」なんて思ってもみたりするのである。