hirax.net::Keywords::「次元」のブログ

■iMはドラえもんの夢を見るか?　　

さようなら、ドラえもん

　Appleが出したiMacは「ドラえもん」を意識している、と私は思う。iMacの顔は白く頭は明るいブルーである。手、すなわち、マウスは真ん丸であり、体型も丸い。iMacのお腹にはCD-ROMが内蔵され、ドラえもんのお腹には4次元ポケットがある。顔の真ん中には丸い鼻(林檎マーク)がある。そして、色違いの妹がいる。
　ドラえもん(iMac)は色々なことを簡単にしてくれる(できる)し、部屋に一台いるという感じである。

　というわけでiMacは「ドラえもん」を意識していると思うのだ。iMacのデザイナーが「ドラえもん」を意識したか、あるいは藤子不二雄の未来を感じる力が優れていたのだろう。

iMacとドラえもん
それぞれ、
(http://www.imac.com/imac/media/imac-vr.mov)
と
http://home.hkstar.com/~wanming/doraemon/doraemon.htm
より

　ところで、私の通っていた高校はずいぶんと自由な学風だった。もちろん、私服であった。授業の科目に至っては「近代アメリカ文学」などというものまであった。変わった先生も多かった。
　その変わった先生の中で、サミー本田(一部仮名)先生は黒沢明の話になると(必ずその話になるのだが)、止まらなかった。
　サミー本田の「七人の侍」と「ドラえもん」の共通点から日本人の特性を語る話などは、今でも覚えている。他人に頼るばかりで、自分で戦おうとしない。日本人を駄目にしたのは「ドラえもん」というマンガだと言っていた。サミー本田には、他にも「素晴らしい芸術は完全な自由の中では生まれない」という持論もあった。

　確かに後者については私もそう思うのだが、前者については違う。藤子不二雄の画いた正式な3回目の最終回でものび太は一人でジャイアンと戦って、そしてドラえもんは未来へ帰って行った。また、fakeではあるがドラえもんの最終回（仮）(http://gamella.elcom.nitech.ac.jp/~satoh/doc/ware/dora.html)でものび太は自分の力で道を開くのである。fakeを例に出すのも、それが「ドラえもん」の生んだ文化であるという観点からすれば、構わないだろう。

　「ドラえもんとの共通点」という観点から、iMacというコンピュータには私は非常に感じる所があるのだ。夢のような話だが、何のために技術者になったのか、何を作りたいのかなどと色々考えてしまうのだ。

　

■微小4次元計測をしてみたい　

デジタルカメラ、実体顕微鏡、動画の三題話

最近はデジタルカメラ(以降、デジカメと呼ぶ)が大流行りである。実験の記録に使うと大変便利だ。ところで、実体顕微鏡の接眼部からデジカメで撮影するという話題が

• 今日の必ずトクする一言「デジタルカメラで超望遠、超接写のナゾ」 ( http://www.bekkoame.or.jp/~jh6bha/higa9801.html#980130)

の辺りにある。この撮影法の難しさは、デジカメの種類によって違う。例えば、FujiFilmのFinePix700では光軸合わせに結構苦労する。ところが、ソニーの「DigitalMavica（技術者向けのオプション(例えばオシロスコープ・フード)などもあって便利）」ではこの撮影方法はとても簡単である。「Mavica」のレンズを実体顕微鏡の接眼部に合わせるだけで、視野をうまく合わせることができる。

といっても、実体顕微鏡にはCCDなどを接続してあることが多いため、単に実体顕微鏡の接眼部をデジカメで撮影するだけでは面白味が少ない。もちろん、高いCCDカメラの代りにメガピクセルのデジカメを使えるメリットは大きいとは思う。

しかし、実体顕微鏡(双眼式)で何が良いかといえば、立体に見えることである。しかし、CCDカメラの接続は一眼式になってしまう。これまで、一つの実体顕微鏡に2つのCCDを接続できるような実体顕微鏡は見たことがない。そこで、接眼部からデジカメ撮影をする方法なら、立体撮影をすることができるので、実体顕微鏡の長所を生かすことができる。

これがそのサンプルである。交差法と平行法の両方を示す。立体に見えるはずである。

交差法 (寄り眼バージョン)

平行法 (ロンパリバージョン)

それでは、3次元計測を行ってみる。まずは、マーキングをする。基板上とICチップ上にA,B,C,Dという4つのマーキングを行う。

計測のためにマーキングしたもの(配置は交差法)

奥行き方向(Z方向としておく)に違いがある場合には、左右の画像でX方向のずれが生じる。そのずれ量を計算してやれば、Z方向の計測を行うことができる。つまり3次元計測を行うことができる。

左右の画像それぞれのマーキングの(x,y)座標

左	X	Y	右	X	Y
A	124	33	A	133	35
B	13	55	B	22	55
C	136	167	C	144	167
D	101	100	D	99	102

左右画像の(x,y)の差をとり視差を出す。すると、(A,B,C)とDの間で違いが有り、Z方向の距離が違うのがわかる。

左右のマーキングポイントの視差

左-右	X	Y
A	-9	-2
B	-9	0
C	-8	0
D	2	-2

この結果から、(x,y,z)を描くと以下のようになる。x-y座標上にzの値を書いてある。Dのポイントのみがz方向に近いのがわかる。

マーキングポイントの(x,y,z)座標

もちろん、本来は光学系から係数などを導くのだが、今回は行っていない。大雑把な説明である。また、同じようなやり方で、3次元表面計測も行うことができる。

ソニーの「DigitalMavica」の素晴らしい所は光軸合わせが簡単なだけではない。動画をmpegファイルとして撮影することができる。というわけで、2台買えば実体顕微鏡の画面を立体動画として保存できる。それが微小四次元計測である。

残念ながら、今回は1台しか使えないので、動画サンプルを示すだけである。mpegファイルをgifに変換したものを以下に載せておく。TFT液晶の拡大画面である。映像の終わりで実体顕微鏡の接眼部からカメラを外しているのがわかると思う。

動画サンプル MPEG形式 507kB
動画サンプル GIF形式155kB (上を縮小したもの)

その他関連情報

• デジタルカメラ大実験(http://www.asahi-net.or.jp/~gg9m-knst/digicame/index.html)

■画像ノイズ解析について考える　

考える理由

　画像ノイズ解析を目的として、2次元フーリエ変換を用いて周波数解析をすることが多い。かねがね、このやり方について疑問を感じていたので少し考えてみたい。

　その疑問とは次のようなことである。

• 通常の2D-FTでは、入力データ全領域での周波数解析を行う。従って、単発のパルスのようなノイズはバックグラウンドに埋もれてしまい、結果にはなかなか出てこない。
• 同じ理由で、2D-FTでは位置と周波数解析を同時に行うことができない。(もちろん、短時間フーリエ関数を使えば、そのような測定は行うことができる。)
• また、ホワイトノイズのようなフラットな周波数特性を持つノイズもバックグラウンドを押し上げるだけの効果しか持たないため、解析をしづらい。

　そこで、今回は単純な画像に対して、2D-FTと2D-離散Waveletの比較を行うことで、2D-FTを用いた「画像ノイズ解析」の問題について考える。

2D-FTと2D-Waveletの例

　はじめに、2D-FTと2DWaveletの例を挙げる。まずは2D-FTである。

2D-FTの例(左から原画像、2D-FT結果、2D-FT結果の鳥瞰図)

　左の原画像は45度のスクリーン角のラインである。2DFTの結果にはその角度方向にピークがいくつか並んでいる。それぞれのピークの中央からの距離が周波数を示している。それはX,Y方向いずれについても言える。今回の場合はX,Y方向のスクリーンの周期が等しいため、2DFTの結果でも45度方向になっているのである。
このように、2D-FTの結果というのは周波数(X,Y両方向)と振幅がわかる。ここでのスクリーン角のような周期性を持つものの解析にはフーリエ解析というのは極めて有効である。店で見かけるインクジェットプリンターもヘッドの移動による周期ムラが激しいが、このようなムラに対してフーリエ変換を用いた周波数解析を行うのは正当であり、有効だろう。

　それでは、同じ画像に2D-Waveletをかけてみる。2D-Waveletの結果は位置と周波数強度分布情報(ホントは違うのだが)が両方出てくる。位置情報が2次元で周波数強度分布情報が1次元であるから、合わせて3次元である。そのため、表示に一工夫いる。
　第一段階として高周波成分から調べてみる。すぐにこの結果の意味がわかるだろうか？

2D-Wavelet例(左が原画像、右が一段階Waveletをかけた結果)

かなり判りづらい。この右の結果は4つの領域にわかれているが、以下の表のような意味を表している。また、いずれも灰色の部分は強度が弱く、白と黒が強度が強いことを示している。

高周波のX成分	高周波成分
低周波成分	高周波のY成分

　低周波成分が原画像と同じようであるのがわかると思う。これは2DFTと違い、Waveletでは位置情報もそのまま保持されているからである。次に、この低周波成分に対して、もう一段Waveletをかけるとこうなる。　右上から左下への対角線上のが周波数成分を示し、これで周波数成分にして3分解できたことになる。右上が一番高周波成分。その左下が次の高周波成分。右下が低周波成分である。
　もう何分割かしてみる　このようにして、画像内での位置と周波数成分が両方ともわかる。

　なお、フーリエ変換では基底関数としてSinが用いられるが、Wavelet変換では基底関数としていろいろな関数を使うことができる。今回はDaubechiesの4次のものを用いている。下がその形である。

Daubechiesの4次のフィルター

ドットのノイズを解析してみる

　それでは、今回の本題に入る。以下が原画像である。左が「2つの大きなドットからなる」画像であり、右がそれにノイズの加わった「ノイズ」画像である。ここでノイズはホワイトノイズを加えているつもりである。ドットは周期性を持つデータだが、ノイズ自体は周期性を持たない所がミソである。また、ここで言う「ノイズ」とは現実の現象とは何ら関係がない。単なる例えである。

ドット画像(左が原画像、右がノイズを加えた画像)

　まず、この2つの画像に対して、それぞれ2D-FTをかける。

２次元離散フーリエ変換を行った結果

　このグラフではXY軸とも-πからπまでの領域で示している。中央からの距離が周波数を示しており、明るいほどその周波数帯の振幅が大きいことを示している。つまり、任意の周波数帯の強度がわかる。
　右のノイズの加わった画像の2DFTの結果では、広い周波数領域で強度が上がっている。しかし、下の鳥瞰図で示した(私は立体が好きなのだ)方でもわかると思うが、バックグラウンドが持ち上がっているだけである。いずれにせよ、あまり左右の間で違いはない。今回のような64x64の画像ではなく、もっと大きい画像ではその違いははより識別不能になる。

２次元離散フーリエ変換の結果を鳥瞰図で示したもの

　さて、次に2D-Waveletで同じように計算をしてみる。下が計算結果である。どうだろうか、ノイズ(位置も周波数も)が一目で判るようには思えないだろうか？

2D-Waveletによる解析結果(左がノイズ無し、右がノイズ有り)

　今回は、自分の頭を整理するために、ただ2D-wavelet変換をかけてみた。まだまだ話しは続くのである。

■分数階微分の謎　

線形代数、分数階微分、シュレディンガー方程式の三題話

分数階微分？

InterLabの1999No.5を読んでいると面白い記事があった。いわき明星大学理工学部の榊原教授の「Waveletと数式処理ツール」という記事である。といっても、興味を持ったのはWaveletのことではない。もちろん、Waveletに興味がないわけではない。この榊原教授が講師を務めたWavelet講習にも参加したこともある。しかし、今回興味を惹かれたのはその記事中にあった「分数階微分の解析」である。

InterLabの榊原教授の記事を引用すると、-通常微分・積分は整数回実行できるが、分数階微分はこれを分数に一般化したものである。さまざまな物理や工学の現象の記述に使われるようになった-とある。一階微分とか二階微分というものはよく使うが、0.5階微分などというものは使ったことがない。どのようなモノなのかさえよくわからない。

参考：

• InterLab (http://www.inter-lab.gr.jp/)

一体、どんな物理や工学の現象の記述に使われているのか知りたくなったので、infoseekで調べてみる。すると、

いわき明星大学の清水・榊原研究室の「粘弾性動モデル」が引っ掛かる。

参考：

• いわき明星大学清水研究室 (http://www.iwakimu.ac.jp/lab/nshimlab/siricon.html)

衝撃吸収・シリコーンの弾性率などに興味を持っている人には面白いかもしれない。

もう少し調べてみると「バナッハ空間バナッハスケールにおける分数階積分作用素」というようなキーワードも引っ掛かる。

そこで、まずは勝手に分数階微分について考えてみた。

分数階微分・積分の勝手な想像図

まずは、イメージを考えるためにグラフを作成してみる。x^2の関数、および、それを微分・積分した関数である。微分は3階まで、積分は2階まで行っている。

図.1:x^2を微分(3階まで)したものと、2階まで積分したもの

このグラフ形式の表示をちょっとだけ変えてみる。

図.2:x^2を微分(3階まで)したものと、2階まで積分したもの

ここまでくると、平面グラフにしてみたくなる。つまり、微分・積分の階数を離散的な整数値でなく、連続的な値としてのイメージに変えたくなる。

図.3:x^2を微分(3階まで)したものと、2階まで積分したもの

これで、微分・積分が整数階でない場合のイメージ(勝手な)ができた。微分・積分が離散的なものではなくスムーズにつながっているものであるというイメージである。図.2から図.3への変化をよく覚えていてほしい。

といっても、これは数学的なイメージのみで物理的なイメージはまだここでは持っていない。位置、速度、加速度などの微分・積分で選られるものに対して同じようなイメージを適用すると、位置なんだけれどちょっと加速度っぽいもの、とか、速度と加速度の「合いの子」みたいなものというような感じだろうか？

さらに、これから先は、f(x)という関数が示す無限個の値を位置ベクトルと考えて、f(x)というのは無限次元空間の一つの点だというイメージを持つことにする。線形代数を考えるならそれが一番わかりやすいだろう。任意の階で微分された関数群が集まって、さらに高次元の空間をなしているというイメージである。

分数階微分を調べる

勝手なイメージはここまでにして、手元にある数学の参考書の中から手がかりを探してみた。すると、
大学院入試問題解説 - 理学・工学への数学の応用 - 梶原壌二 現代数学社ISBN4-7687-0190-6
の中に手がかりがあった。あれ、ということは以前にやったはずなのか...そう言えばおぼろげな記憶がちょっと...

その中の言葉を少し引くと、
フーリエ変換は等距離作用素である、関数空間L^2(R)における回転といえる。結局、

ここで、fは元の関数であり、Fはフーリエ変換

となる。そして、古典力学におけるハミルトン関数において、運動量を微分演算子で置き換えれば、量子力学や量子化学のハミルトン演算子が得られ、シュレディンガー方程式などにつながるのである、とある。他の資料を眺めてみると、どうやら量子力学などの分野からの要請に応じてここらへんの微分演算子の分野が発展しているようだ。理論物理などをやった方ならよくご存知のことだろう。例えば、水素原子の基底状態の波動関数へ運動エネルギーの演算子を作用させるというような、基本的な所でも、このフーリエ変換を用いた微分演算が用いられてる。

さて、この式自体は非常に簡単である。それにイメージも湧きやすい。
i を掛ける演算、私のイメージでは複素数空間の中で90度回転をする(言い換えれば、位相が90度ずれる)演算、が微分・積分であるというイメージはスムーズに受け入れやすい(それが正しいかどうかは知らないが)。なぜなら、微分が空間の中での回転であるとすると、三角関数の微分・積分に関する性質(例えば、Sinを微分するとCosに、Sinを2階微分すると-Sinになる、すなわち、一回の微分につき位相が90°ずつ回転する(位相がずれる)というような性質)が納得でき、それがフーリエ変換という形で登場してくることがスムーズに受け入れられるのである。また、微分といえばとりあえず三角関数の登場というイメージもある。

　もう少しわかりやすく書くと、

• 三角関数では一階微分の結果は90度位相がずれる(回転する)。
• ならば、(例えば)0.5階微分は45度位相をずらせば良い。
• 任意の関数もフーリエ変換により、三角関数に分解される。
• ならば、任意の関数に任意の実数値の微分が成立する。

ということである。

　任意の関数をフーリエ変換し三角関数に分解した時の位相、言い換えれば、周波数領域での位相ずらし、で分数階微分が定義されるということは、物理的実用的に大きな意味を持つ。例えば、電磁波、弾塑性運動などの物理現象の中での位相変化を分数階微分で解けることになる。例えば、複素貯蔵弾性率などについて分数階微分との関係は深そうである。あるいは、媒体中の電磁波の位相などについて適用するのも面白そうである。

分数階微分を使ってみる

よく分からないところも多いが、とりあえず、

という式を使ってみる。まずは、使ってみないとわからない。とりあえず、1次元の関数を作成して、この式を適用してみる。まずは、よく出てくるガウス分布で適用してみる。まずはガウス分布とそれの通常の一階微分の解析解を求める。

ガウス分布(左)とその一階微分の解析解(右)

それでは、今回の方法による一階微分の結果と、それと解析解との比較を示す。なお、本来無限領域のフーリエ変換を有限の領域で行っているため、端部近くで変なことが生じるのはしかたがないだろう。また、色々な事情により係数の違いは無視して欲しい。

フーリエ変換を用いた方法(左)と解析解(右)の比較

ちょっとずれが生じているが、こんなものだろう。しかし、これだけでは今回のフーリエ変換を用いた微分の面白さはでてこないので、0から2の範囲で連続的に分数階微分をしてみる。

ガウス分布の0から2の範囲における連続的な分数階微分

1/10 (=0.1)階微分	1/2 (=0.5)階微分	7/10 (=0.7)階微分	1階微分
13/10 (=1.3)階微分	15/10 (=1.5)階微分	17/10 (=1.7)階微分	2階微分

モーフィングのようで面白い。

さて、今回は分数階微分を勉強してみる所までで、これの応用は別に行ってみたい。もちろん、言うまでもないと思うが、間違いは多々あると思う。いや、田舎に住んでいるもので資料がないんですよ。

■分数階微分に基づく画像特性を考えてみたい　

同じ年齢でも大違い

前回、分数階微分の謎 - 線形代数、分数階微分、シュレディンガー方程式の三題話- で分数階微分について調べた。例えば、0.7階微分といった、整数階でない微分である。今回はそれを使った応用を考えてみたい。

人間の視覚というものは明るいものは強く感じることができる。これは当たり前である。そして、それだけでなく、強さが変化している所にも(興味を)強く感じ取るようになっている。岡本安春氏の「Delphiでエンジョイプログラミング」によれば、そのような考えはLaming(1986)がdifferential coupling(差動結合)として発表しているらしい。

ということは、人間が画像を感じる特性というものは、画像強度と画像強度変化(画像強度の一階微分)の中間的なものであると言うことができるかもしれない。とすれば、分数階微分を導入すれば面白い表現ができるかもしれない。
今回は、そういう考えのもとに分数階微分を用いて人間の画像特性について考えてみたい。

まずは、元画像を示す。元画像はガウス分布に基づいて作成されたものである。

元画像とその鳥瞰図

まずは、左の元画像を見て欲しい。どこに強い感じを受けるだろうか？白い部分はもちろんであるが、白と黒の境界部にも強い感じを受けるだろう。ギザギザになっているのはデータが少ないからなので、無視して欲しい。というわけで、人間の視覚画像特性は

• 画像強度
• 画像強度変化(画像強度の一階微分)

というものの中間的なものと結び付けることができる(としておく、今回は)。それでは、元画像から元画像の一階微分までの間で連続的に分数階微分をしてみる。先の元画像を見たときに受けた印象と近いものが、分数階微分画像の中にあるかどうか探してみてもらいたい。

元画像から元画像の一階微分までの分数階微分画像

元画像
1/2階微分画像
15/20階微分画像
1階微分画像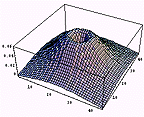

白地に黒画像バージョンも示しておく。紙の上の画像に慣れた人にはこちらの方が良いだろう。

元画像から元画像の一階微分までの分数階微分画像(白地背景)

元画像

1/2階微分画像

15/20階微分画像

1階微分画像

なお、今回の画像の作成は次のような手順で行っている。

1. 1次元のガウス分布を作成する。
2. 微分値が正であるような半分の領域を線対称に回転させ、2次元画像を作成する。

なぜ、このような方法をとっているかと言えば、微分値が負の値になる領域を除きたいからである。

今回は

• 画像強度
• 画像強度変化(画像強度の一階微分)

というものの中間的なものとして分数階微分を用いたが、これに限る話ではない。例えば、

• 電位
• 電界(電位の微分、といっても本来は電位が電界の積分か)

とか、あるいは、

• 人口密度
• 人口密度変化(人口密度の微分)

といったものでも良いだろう。今回のデータを電位とか人口密度に基づくものとして読み直せば良いだけである。色々と用途があるのかもしれないと思う。分数階微分の定義からすれば、位相遅れなどが存在する物理現象であれば、物理的な意味を厳密に持たせた上での解析ができるように思う。いずれ、音響インピーダンスなどの解析に用いてみたい。

さて、分数階微分を調べる中で、バナッハ空間についても調べた。調べ始めた時には、聞き覚えもなかったが、調べてみるとヒルベルト空間の導入で登場していた。きれいさっぱり忘れていたようである。
京大数学教室 徳永健一氏のWEB (http://www.kusm.kyoto-u.ac.jp/~kenichi/)
から辿れる「「年齢の本」数学者版」によれば
バナッハがバナッハ空間を提唱したのは30歳の時であるらしい。(http://www.kusm.kyoto-u.ac.jp/~kenichi/age/30.html)
うーん...