1999-02-26[n年前へ]
■ヒトは電磁波の振動方向を見ることができるか? 
はい。ハイディンガーのブラシをご覧下さい
(1999.02.26)
リチャード・ファインマンの本の中で次のような問題があったように思う。
「偏光板がフィルターが一枚だけある。その偏光フィルターの偏光方向をどのようにして知れば良いか?」
その本の中での答えは、
「物体の反射光を偏光フィルターを通して見てみる。」
だった。ブルースター角で入射した光の反射光は、入射面に対して電場の振動方向が垂直になっている、ということを利用するわけである。
分かりやすいように、偏光フィルターを通してみたガラスの反射光をデジカメで撮影してみる。左が反射光を通すような角度に偏光フィルターを回したものであり、右が反射光をカットするような角度に偏光フィルターを回した場合である。この左の場合、すなわち、反射光が一番通過している角度から液晶の偏光面がわかるわけである。
 |  |
ところで、このようなファインマンが示したような方法を用いなくても、そもそもヒトは電磁波の振動方向を見ることができるのである。以前、「渡り鳥の秘密- 3000kmの彼方へ - (1999.01.30) 」の中で「鳥は太陽の位置、光の偏光パターンを位置のセンサーに使う」という話があった。ヒトも同じく光の偏光方向、すなわち、電磁波の振動方向を見ることができるのである。鳥はどう見えるかは私にはわからないが、ヒトならば自らが実験台になれるので、電磁波振動方向をどう見ることができるか調べてみたい。というわけで、「渡り鳥の秘密- 3000kmの彼方へ - (1999.01.30) 」の中で「近日中にある実験をする予定である」と書いたものが今回の確認実験である。なお、光の進行方向と磁界の振動方向を含む面を「偏光面」、電界の振動面を含む面を「振動面」と呼ぶ。
電磁波の振動方向をヒトが見ると「ハイディンガーのブラシ "Haidinger'sBrushes"」というものが見える。それを知ったのは、いつものごとく「物理の散歩道」からである。網膜に複屈折性があるために「ハイディンガーのブラシ」が見えるのだという。
私はこれまで、「ハイディンガーのブラシ "Haidinger's Brushes"」を見たことがない。いや、正確に言えば意識したことがない。そこで、判別しやすいように直線偏光を用意してやることにした。そこで、東急ハンズで偏光フィルターを買ってきた。
そして、空を見てみる。もちろん、偏光の偏りが強い、太陽を中心にして90度の角度をなす同心円方向である。詳しくは、
- 可視-赤外域での偏光観測による衛星観測手法の開発基礎研究(http://www.mri-jma.go.jp/Dep/sa/Lab1/labt01-s.html)
- エアロゾル観測(http://mars.im.kindai.ac.jp/KISYO/YPROJECT/kansoku.html)
さて、ヒトである私は、空を眺めて格闘すること5分程で、「ハイディンガーのブラシ"Haidinger's Brushes"」がわかるようになった。私が見たハイディンガーのブラシ"Haidinger's Brushes"を示す。
 |
この絵で太陽の方向は右上であり、偏光面は次の絵の青の矢印方向になる。
 |
というわけで、ヒト(少なくとも私は)電磁波の振動方向を見ることができるのである。慣れてしまうと、白い紙を見つめているときなども(条件によっては)見えるようになる。色を扱う人は意識すると面白いと思う。
ところで、偏光フィルターがどういうものか知らない人のために、NotePCの液晶に偏光フィルターを重ねた写真を示す。
 |  |
なぜ、こうなるかわからない方は、
などを参考にして欲しい。液晶ディスプレイの構造がわかると思う。そして、面白いことに気づいた。NotePCの液晶からの光は直線偏光である。ということは、NotePCの液晶にはハイディンガーのブラシが映っているのである。正確に言えば、NotePCの液晶を見ているあなたの視界の中央には、ハイディンガーのブラシが映っているのである。と、気づいてみると確かに見えている。
というわけで、液晶ディスプレイを使用している方はハイディンガーのブラシを見て頂きたい。以下のやり方がわかりやすいと思う。
1.このWindowを最大化する
2.下へスクロールして画面を真っ白にする。
3.液晶ディスプレイ(NotePC)を回転させる。
4.画面(視点)の中央に(視点に対して位置が)動かない黄色いもやが見えるはず。もちろん、回転はする。
液晶ディスプレイやヘッドマウントディスプレイ(HMD)を色々見てみたが、どれにもハイディンガーのブラシは存在していた。視界の中央に不思議な十字架のように現れているのである。現代の液晶技術が負う十字架である。
誰もが、目の前にあるのにそれに気づかないというのも、実に面白い。まるで、「青い鳥」のようである。そして、そういうことはとても多いのではないかと思う。それはそれで面白い話だ。
- それでは、ハイディンガーのブラシをご覧下さい -
1999-07-05[n年前へ]
■目に映る明るさって何ですか? 
君は天然色
前回、デジカメ画像をスクリーンセーバーにしたい-記念写真を飾ろう - (1999.06.30)
を作るために、いくつか調べ事をした(ホントはずっと昔に)。それについてまとめておきたい。
調べたことは、
- カラーから白黒への変換はどうする?
- セピアカラーって一体何だ。
- セピアカラーへの変換はどうやろう?
カラーから白黒への変換はどうする? どうしよう? これは結構難しい問題(結果的にやったことは簡単でも、プロセスとしてはすごく難しい)だ。そうそう白黒の世界を見たことのある人はいないだろう。特殊な状況下(たとえば、すごく暗い所とか)では色を感じないこともあるだろうが、普通の世界は天然色である。フルカラーの世界だ。そもそも明るさって一体何だ?(明快に答えられる方教えてください。) 例えば、下の図で明るい順番はどうなっているだろうか?自信を持って答えられるだろうか。
 |
とグチを言っていてもしょうがないから、決めてしまおう。うす暗い(1lx程度)部屋で景色を眺めてみよう。その時見える世界が、明るさの世界だ。そこには色など存在しない。確かめて欲しい。今回は、とにかくそれを「明るさ」の尺度としてしまおう。
(興味ある方は明るさを測ろう- 新技術の女神 -(1998.11.13)もご覧下さい)
次に明るい部屋へ移動する。そこでは、新たなものが加わる。それが「色」である。ということで、「明るさ」+「色」で世界を表現することにしよう。
いきなりではあるが、人間が光を感じる網膜内の光受容器には錐体と桿体がある。
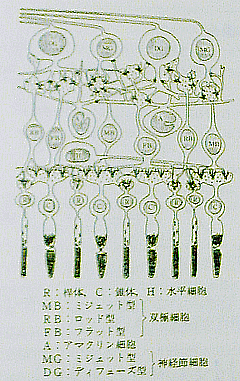 「視覚と画像」 大頭・行田 著 森北出版より |
それでは、明るい部屋で感じる色はどうなっているだろうか。色を感じる錐体の中には波長感度の異なる3種類の視物質がある。それぞれの波長感度を以下に示す。
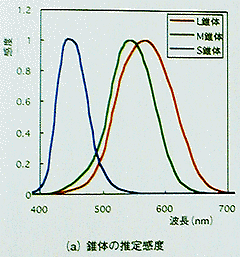 CQ出版 洪 博哲著 「お話・カラー画像処理」より |
次に、それらの3種類の視物質による錐体が組み合わさった時の波長比視感度を以下に示す。点線で示してあるほうは比較的暗い場所での波長比視感度なので、今回は無視して欲しい。
 「視覚と画像」 大頭・行田 著 森北出版より |
後は、このグラフを元に赤、緑、青の3点で重み付けしてやれば良いだろう。
というわけで、グレー化のために使っているのはこの式だ。
- Red: ptr[2]
- Green: ptr[1]
- Blue: ptr[0]、として
やっと、ここまで辿りついた。結局使うのはこんな簡単な式なんだ、っていうツッコミは無しにして欲しい。同じ式を使うのでも、私はそこまでのプロセスも重視したいのだ。
さて、こういった色を扱う話題であれば、脇色彩研究所のWEB(http://www.mmjp.or.jp/rwicp/ )中から
- 色に対する感じ方(眼とフィルム)( http://www.mmjp.or.jp/rwicp/data106.html )
- カラーフィルムの特性と色再現( http://www.mmjp.or.jp/rwicp/filmirosai.html )
- 明るさの見え方(明暗対比)( http://www.mmjp.or.jp/rwicp/data506.html )
- 色覚、眼の色に対する感じ方( http://www.mmjp.or.jp/rwicp/data509.html )
また、文中でも書いたが、「明るさとは***ということだ」と明快に答えられる方は私に是非教えて頂きたい。もし、素晴らしい答えが頂けたら、粗品(言葉通りの)を進呈しても良いと思っているくらいだ。
なお、以下のような答え方は遠慮致したい。
例1:
私 「液体と固体はどう区別するの」
A 「融点を境にして上と下」
私 「....」
例2:
私 「クジラは哺乳類、魚類どっち?」
A 「卵生まないから哺乳類」
私 「...」
1999-08-09[n年前へ]
■色を伝える時に、考え忘れていたこと(色弱と色空間 その1) 
We can work it out!
オプトニューズ (1999) No.4の光の話題に三楽病院の岡島修氏が「レーザポインタと色覚異常」という小文を書いている。色弱の人の感じ方とプレゼンテーション(特にレーザポインタの色)に関する提言である。それを読んであることを思い出した。何年か前、Labofinder(Macintoshを科学分野で使うユーザーグループ)でプレゼンテーションについて特集していた発表会だったと思う。どなたかが発表を行った後に、次のような質問があった。
「私は色弱なのですが、プレゼンテーションを行う際に使う色などについて、そのような人を意識して作成されているでしょうか?」
恥ずかしいことに、私はあまり考えたことがなかった。そして、本WEBを作るに際してもそういった点はおろそかになっていると思う。そういう自分自身への反省を込めて、色弱と色空間について考えてみたいと思う。
まずは、色弱に関する情報を調べよう。
- COLOR HANDICAP( http://www.sakuranet.or.jp/~tks/color/text/ )
- からーふぃくしょん( http://sun.endless.ne.jp/users/tanafic/ )
- Dr.MeMeの おめめ講座 (http://www.so-net.ne.jp/vivre/eye/ )
それでは、私なりの理解と考察を始めてみたい。
目に映る明るさって何ですか? - 君は天然色- (1999.07.05)
の回で触れたが、人間が光を感じる網膜内の光受容器には錐体と桿体がある。この内、色(すなわち光の波長方向に関する感じ方)を感じるのは、錐体の働きによるものである。錐体には3種類有り、
- L錐体 -> 赤
- M錐 -> 緑
- S錐体 -> 青
目に映る明るさって何ですか? - 君は天然色- (1999.07.05)
を参照のこと)。それらの錐体に異常がある時に、色弱もしくは色盲が発生する。
| L錐体 (赤) | M錐体 | S錐体 | 先天性色覚異常の分類 |
| O | O | O | 正常 |
| X | X | X | 桿体1色覚 (全色盲) |
| O | X | X | 錐体1色覚 (赤) |
| X | O | X | 錐体1色覚 (緑) |
| X | X | O | 錐体1色覚 (青) |
| X | O | O | 第1色盲 (赤色盲) |
| O | X | O | 第2色盲 (緑色盲) |
| O | O | X | 第3色盲 (青色盲) |
| OX | O | O | 第1色弱 (赤色弱) |
| O | OX | O | 第2色弱 (緑色弱) |
| O | O | OX | 第3色弱 (青色弱) |
この図中でOは正常、Xは欠損、OXは機能低下である。
M,L錐体に関する異常はX染色体劣勢遺伝をする。また、錐体1色覚、および、S錐体に異常がある第3色盲・第3色弱は比較的少ないという。
それでは、これらの錐体に異常があるとどのような色を識別できなくなるのだろうか? 私は先に挙げたようなWEBを読んだくらいの知識がないので、数学的な考察をおこなってみる。現実をよく知らないため、実際の症例とはかなりの違いがあるかもしれない、ということは先に断っておく。
現実の症例の参考としては、岡島修氏の「レーザポインタと色覚異常」中に挙げられているCIEXYZ表色系における強度色覚異常者(第1異常、および、第2異常)の混同色を用いる。その図を加工し、XY色度図を重ねたものを以下に示す。それぞれの図において、白い直線上の色を混同してしまうのである。
 |  |
今回は、通常の(Red,Green,Blue)データを基本として考える。PCなどで表示を行う際に一番よく使うからである。任意のRGBデータをCIEXYZ表色系に直すためには、
WEBページは会社の顔色 -WEBページの色空間を考える2- (1999.04.26)
で用いたハイビジョンTVの色空間を例に用いて、
- X= 0.412391R + 0.357584G + 0.180481B
- Y= 0.212639R + 0.715169G + 0.072192B
- Z= 0.019331R + 0.119195G + 0.950532B
- x=X/(X+Y+Z)
- y=Y/(X+Y+Z)
それでは、通常、第1色盲(赤色盲)、第2色盲(緑色盲)の3種類についてxy色度図の計算例を示してみる。ある錐体に異常が存在する場合に、どのような色空間が再現されるかの計算を行ってみる。通常のxy色度の位置において、ある錐体の刺激を無くした場合に色がどう変化するかを示したものである。であるから、第1色盲(赤色盲)、第2色盲(緑色盲)においては通常使われるxy色度図とは異なるものになる。また、ここで示した色が色弱の人が見ている色という意味でもない。
単純に、ある錐体が得るであろう情報を無くしたときに、情報の識別がどのように困難になるかを確認した、と言った方がいいかもしれない。
また、本来3錐体の波長感度特性はRed,Green,Blueの単波長というわけでもない。しかし、今回は簡単のために、3錐体の波長感度特性はRed,Green,Blueの単波長であるという仮定の元に計算を行っている。そのため、かなり現実とは違う結果になっている。近々、きちんとした計算をするつもりである。
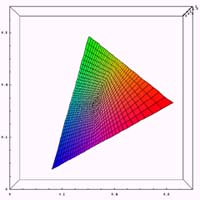 |  | 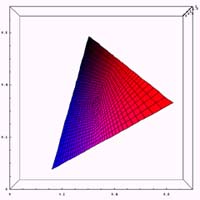 |
ここでは、Z方向(明るさ方向)に対して無視を行っているので、かなりの誤差が存在すると思う。また、計算の中で一つの錐体に異常があるときの、RGBデータの再配分を計算する部分に極めて大雑把な近似をおこなっているので、その部分でも誤差が大きいと思う。
また、Red,Green,Blueの三色により色空間を形成しているため、各点を頂点とする三角形内に色空間は収まることになる。
この計算結果を眺めながら、岡島修氏の「レーザポインタと色覚異常」中に記述されている色弱における混同しやすい色の例、
- 第1色盲
- 赤と黒
- ピンクと青
- 第2色盲
- 赤と緑
- オレンジと黄緑
- 緑と茶
- 青と紫
- ピンクと白
- 緑と灰色
例えば、通常の色空間において赤(すなわち右上)の場所を第1色盲の色空間の中で見て欲しい。黒との識別が困難なのは一目瞭然だろう。また、下の図に示すように、通常の色空間でピンク(1)と青(2)が第1色盲の色空間の中でどうなっているかを見れば、
 | 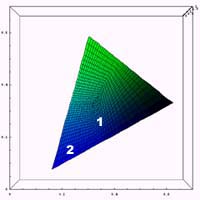 |
これも1と2の識別が困難であることが容易に想像がつく。第2色盲でも同じように見てみて確認して欲しい。
なお、上の図中で中心部が暗くなっているが、それはグリッド線のためであり、本来の色はもっと白っぽい色である。また、今回は岡島修氏の「レーザポインタと色覚異常」中の図と比較するために、CIExy色度図を用いたが、もともとxy色度図は人間の感じ方とは結びつけにくい。いずれ、均等色空間における解析を行うつもりである。また、先に記述したようにきちんと錐体の波長感度特性を考慮に入れた計算をするつもりである。今回はあくまでごく簡単な実験である。
というわけで、今回は色弱の方がどのような色空間を感じているかを考察してみた。今回の話中には色々間違いもあると思う。なにか訂正すべき情報を見つけてくださったら、教えて欲しい。
画像出力に携わる方でこのWEBをご覧になっている人もいるはずだ。色を正しく伝えることを日夜考えている人もいるだろう。しかし、色を正しく伝えることを考えるときに、考え忘れていることはないだろうか? 「正しい伝え方」は、誰にとって「正しい」のだろうか?私達が当然のように感じている色についても、異なる感じ方をする人のことを考え忘れてはいないだろうか?
そういった人は少数だと言われる方もいるかもしれない。しかし、あなたが当然の権利のように享受しているものは果たして全ての人が得ているものだろうか? もしかしたら、その権利を享受している人の方が少数派であるものもあるのではないだろうか?
やることは至極簡単なことだ。技術的に言うならば、人の知覚も「デバイスの一部」として考えた際に、「人の知覚」が数種類あるものとして、異なるデバイス間のカラーマッチングを考えれば良いだけのことだ。もちろん、一筋縄ではいかないだろうが、得られるものの大きさからしたら、やってみる価値はあるだろう。
プレゼンテーションソフト、あるいは数多くのソフトウェアにそういったことをきちんと考えたテンプレートが現れ、WEBサイトの色、画像機器のカラーマネジメントにそういった「全ての人(健常者と呼ばれる人のモデルだけでない)の感じ方まで含めたカラーマッチング」が適用されていく日も必ず来るはずだ。もしかしたら、このWEBサイトに来ている人の中には、今すぐにでもそういうことを始めることが出来る人もいるかと思う。果たして、そんなことが「できるかな?」と思われる人もいるかもしれないが、きっとできる筈だ。
こういったことは色覚に限る話ではないと思う。考え忘れていることは数多くある。できることも数多くある、と私は思う。
2004-03-15[n年前へ]
■巨乳ビジョン・シンドローム 
「人の視覚は7メガピクセル」編
デジタルカメラの高画素化が急速に進んでいる。定価が数十万円ほどにもなるデジタルカメラであると、使われているイメージセンサの画素数は10メガピクセル(=一千万画素)近くになるし、定価が数万円の普及価格帯のデジタルカメラでも数メガピクセル(=数百万画素)であるのが普通である。そして、最近だと携帯電話に付属しているカメラでさえ2メガピクセル以上のイメージセンサを使っているものすらある。35mmの銀塩フィルムが40メガピクセル弱だから、ハイエンド・デジタルカメラの解像度はその数分の一にまで達しようとしている、ということになる。
そんなふうに、デジタルカメラの高画素化は進んでいるわけだけれど、そもそも私たち自身の「目」というのは一体どの程度の画素数があるものだろうか?最近のデジタルカメラと比べると、私たちの目には一体どの位の画素があるのだろう?デジタルカメラと同じ、「メガピクセル」を単位にするならば、人間の「目」というのは何メガピクセルに相当するのだろうか?
実は、人間の場合、デジタルカメラのイメージセンサの画素に相当するのが、目の中の網膜上の錐体(色を感じ、網膜の中心部に多くある)である。その数はおよそ700万個弱ほどもある。つまり、デジタルカメラと同じように言えば、人間の目は7メガピクセル相当ということになる。ということは、最近の数十万円のデジタル一眼レフカメラでさえ、やっと人間の目と同じ程度の画素数に達した程度なのである。普段生活をしている中では、人間の「目」の画素数なんて気にすることはそうそうないだろうけれど、人間の「目」はやっぱりスゴイのである。そして、そんな人間の「目」と同じレベルになりつつあるデジタルカメラもスゴイものなのだ。
ところで、『普段の生活の中では、人間の「目」の画素数なんて気にすることはそうそうない』と書いた。確かに、人間の「目」の画素数や配置、つまり、人間の「目」の画素、網膜上の錐体の数や配置などを気にすることはまずないかもしれない。けれど、それを意識しなくても実は目にしている機会は多いのである。
それは、例えばこんな縞模様を目にするときだ。片目をつぶって、もう片方の目だけでこの下の縞模様を眺めてみよう。すると、色の付いていないハズの白黒の縞模様の上に、うっすらと色の付いた縞模様が重なって見えてくるハズである。もしも、最初のうち判りにくいようであれば、片目をつぶったまま見る距離を変えてみれば判りやすいかもしれない。縞模様がウネウネと動く様子が見えると思う。
これは、「Brewsterの色」と呼ばれる色模様で、網膜上にある「赤、青、緑」の各色を感じる錐体の配置と「白黒の縞模様」が干渉してモアレが発生することで知覚される偽色なのである。
 |
こんな模様というものは実は結構街中に溢れている。例えば、エスカレーターの階段部分やフェンスの金網、あるいは、マンガの効果線など、こういった規則的な模様を普段の生活の中で目にすることは実はとても多い。そんな時、私たちの目はカラフルな「Brewsterの色」を見ていることになる。見てはいるのだけれど、ただそれを意識しないことが多い、というだけである。逆にこんなモアレを意識してしまうようになると、私たちの7メガピクセルのイメージセンサが景色の中の縞模様と干渉して発生してしまうカラフルなモアレは本当に街中に満ちあふれていることに気づくのである。
例えば、規則正しい模様の服というようなものはとても多い。そして、そんな服の上でさえワタシのまなこ(心の眼かもしれないが)はBrewsterのモアレを見いだしてしまうのである。そして、規則正しい模様の服の上にさえBrewsterのモアレを見いだしてしまうようになってしまうと、これが何とも恐ろしい副作用がもれなくオマケで付いてくるのだ。それは、「巨乳ビジョン・シンドローム」という恐ろしいオマケなのである。
その「巨乳ビジョン・シンドローム」の症状は、下の二枚の写真を見てみると判りやすいのではないか、と思う。まず、左は「規則正しい模様のある生地でできた服」を着ている女性である。そして、右の写真はそんな「規則正しい模様のある服」を眺めたときに、意図せずしてモアレが発生してしまった様子を示している。ほとんど同じ二枚の写真ではあるが、よ~く眺めてみれば服の部分にモアレが発生してしまっている様子がわかるハズだ。しかも、ある特定の一部分であることも判るだろう。
を着ている女性  | モアレが発生すると…  |
…そう、規則正しい模様の服を着ている人を眺めた場合には、凹凸の激しい部分で特に顕著にモアレが発生してしまうのだ。そして、そのモアレはその凹凸具合の等高線(と同じようなもの)を示してしまうのである。もっとハッキリ言ってしまうならば、規則正しい模様の服を着ている女性なんかを眺めた場合、胸の部分の凹凸具合の等高線が意図せずして見えてしまうのである*。日夜地図を作り続けている国土地理院もビックリのバスト地図(凸凹等高線入り)が幸か不幸か見えてしまうのだ。しかも、これは凹凸の激しい部分でのみ顕著に認識されたりするがために、巨乳の等高線は容易に見ることができるけれど、微乳の等高線はなかなか見ることができない、というまさに「巨乳ビジョン・シンドローム」なのである。
残念ながら、私はオッパイ星人ではないので詳しいことは判らないけれど、真性のオッパイ星人達は生まれながらにしてこんな巨乳ビジョンのまなこ(眼)を身につけているに違いない。だからこそ、微乳の小胸さんではなくて、巨乳さんに引き寄せられていくのかもしれない。つまりは、オッパイ星人をオッパイ星人たらしめていたのは、こんな巨乳ビジョン・シンドロームだったのかもしれないのである。
そして、おそらく彼らの視力は私たちヒトに比べて遙かに高いハズだ。だから、単に規則正しい絵柄の服だけではなくて、例えば規則正しく糸で織りなされた服、すなわち、それが布製であればどんな服の上からでもこんな等高線モアレを見いだしてしまうに違いないのである。そして、その服を着ているものの胸の凹凸の等高線(もちろんその部分だけではないが)を眺めることができるに違いないのだ。
というわけで、最後に「オッパイ星人の視覚をシミュレートした画像」をでっち上げてみたのが下の動画である。これは、女性が着ている「服の持つ規則性=周期」を自動的に認識し、網膜の周期をその「服の持つ周期]近辺になるように変化させて、意図的にモアレを発生させてみたものだ。どんな模様であってもそれが「規則正しい模様を」である限りは、胸の凹凸の等高線がはっきりと見えてしまうことが実感できることだろう。
 |
というわけで、規則正しい模様の服を着ている女性は周りの視線(オッパイ星人や幸か不幸か「巨乳ビジョン・シンドローム」にかかってしまった人間)に要注意、というのが今日の結論なのだ。そして、邪悪な心を持つ技術者が、「巨乳ビジョン・シンドローム」と同じようなアルゴリズムで動く「巨乳ビジョン・カメラ」を開発しないことを、今はただただ祈るばかりなのである。
2007-08-28[n年前へ]
■今更ながら…のRubyハマり 
これまで、Perlでしていた作業をRubyに変えた。物忘れが激しいので、すでにPerlの文歩を忘れてしまった…ということもあるけれど、データ処理をすることが多い仕事では、Ruby(単にArrayクラスのおかげなのかもしれないが)の方が楽に感じるようになったからだ。
ふと、気づいたことがある。なぜか、ある言語を勉強しようとして、他の言語がわかるようになったことが多いような気がする。Perlを勉強しようとして、始めて、Mathematica が少し理解できるようになった。WebMathematicaは、もちろん、eRbの理解を早めてくれた。そういえば、Photoshopのプログラミング・マクロ記述可能なプラグインを作ろうとして、Perlの作りやMatLabの作りがほんの少しだけ理解できるようになった気がする。
暗い星を眺めようとする時、その星を見つめようとすると、その星は見えなくなる。網膜の感度分布のせいで、どうしてもそんな風になる。だから、暗い星を眺めようとするなら、その少し横を眺めなければいけない。何だか、少しそんな感じだ。
ここ半年に覚えようとしたのは、WebMathematica, Ruby, Rails, Matlab という辺りだ。これらは、何に繋がっているんだろうか。