2000-02-13[n年前へ]
■競馬の写真判定とパノラマ写真 
パノラマ写真と画像処理 Part.2
前回 、
の時にi_matさんから頂いたメールを紹介した。i_matさんは- I*MAT The HomePage (http://www.nsknet.or.jp/~i_mat/ )
- atoz@gol.com (http://www2.gol.com/users/atoz/index.html )
さて、前回
これらのソフトのStack-Slice機能を用いれば「複数画像(動画)からの走査線抽出」ができる。その使用例と、その面白い座標軸変換について考えてみたい。と書いた。今回もまた「数日後には登場」と言った割には時間が経っているような気もする。しかし、ここのところ文字通り忙殺されていたのである。と、言い訳をしながら今回この作業をやってみることにした。しかし、このページは少々重くなってきた。まして、走査線の抽出の話は使用画像が多くならざるをえない。そこで、次回、詳しく使用例を紹介することにする。
よく、次回登場と言ったまま数ヶ月経つことがあるが、今回は大丈夫である。少なくとも数日後には登場することと思う(多分)。
まずは、
- 「複数画像(動画)からの走査線抽出」
- 「座標軸変換」
以下に示す連続の画像は競馬のゴール地点に競走馬が到着した瞬間である。「馬に見えない」という人がいたら、それは目がおかしい。誰がなんと言おうとこれは馬である。馬と鹿の区別がつかない人は馬鹿と呼ばれるが、これはとにかく馬なのである。
 視野の中に馬がもっと入ってくる。
視野の中に馬がものすごく入ってる。 |
さて、このビデオカメラで撮影された画像は例えば以下のようなものである。
 |
撮影された各時間の画像から、この画像の赤で囲んだところを抽出し、並べたらどのようになるだろうか?
それはこのようになるだろう。よくある競馬の着順判定写真である。
 |
一見、これまで眺めてきたビデオカメラで撮影された画像と同じように見えるが、全く違う。ビデオカメラの撮影画像の動画中における、複数画像間の「位置」は全く変化していない。変化しているのは「時間」だけである。
だから、このような赤い長方形の画像を並べた方向というものは「時間軸」を意味しているのである。それを、下の画像に示してみる。
 |
この画像は縦方向は「空間軸」であるが、横方向は「時間軸」なのである。ビデオカメラの画像が縦横共に「空間軸」を示しているのに対し、その一軸を「空間軸」から「時間軸」に変換したものなのである
この競馬の着順判定写真の場合、カメラは空間に固定され「時間軸に変化するもの」を撮影していた。だから、このように各画像から一部を抽出して並べると、それは「時間軸」に対する変化を示すものを得ることができる。
また、例えば実験条件を変えたときの計測画像に対して「各画像から一部を抽出して並べる」ということをするならば、それは「空間軸」x「実験条件」というものを表す画像を得ることができる。
それでは、時間的には変化しないものを、ビデオカメラで撮影する方向を変化させながら撮影したらどうなるだろうか?例えば、ビデオカメラを下のようにして360度回転させながら撮影をしてみるのである。
 |
この場合撮影画像の各画像は撮影方向角度が異なるわけである。従って、先ほどのように一部分を抽出して並べると、一方向は「空間軸」であり、もう片方の軸は「撮影方向角度」になる。結局当たり前ではあるが、ある位置から眺めた周りの景色が得られるわけだ。
これが、前回i_matさんの要望していた
- 8ミリビデオを横倒しにして、 モーター回転するヘッドでぐるりと360度撮影し、
- その撮影した動画ファイルの、各フレームから走査線にして数本分を抽出し(インターレースで256本のうちセンター128本目の前後数本の走査線分)、
- それを貯めて1枚のjpgファイルにする、
- そのJPEG画像をMakeQTVRPanoramaの入力にして、パノラマムービーを作る、
それでは、その作業を実際にしてみようと思う。i_matさんから送って頂いた動画ファイル
を使い- 動画から静止画に変換し(走査線の狭間-1/60秒の世界を目指せ- (1999.07.08) 参照)、
- Image PC(NIH-imageをWindowsに移植したもの)で、走査線の一部を抽出し並べた静止画を作成する
もういきなり結果を出してしまおう。これが、「動画ファイルから走査線を抽出し、パノラマ写真にしたもの」である。
 |
おや?何が何だかわからない画像になってしまっている。変なモザイクがかかったみたいな画像になっているし、グレイ画像である。参考までに、先ほどの動画から手作業でパノラマ画像を作成したものを以下に示す。上の画像と比較してみると画像の示すものの対応がわかるだろう。
 |
さて、今回の実験結果が
- 変なモザイクがかかったみたいな画像になっている
- グレイ画像である
まず、
- 「グレイ画像」になっている理由
そして、「変なモザイクがかかったみたいな画像になっている」のは(動画中の)各画像から走査線をそれぞれ一本しか抽出しなかったからである。だから、横方向(カメラの撮影方向角度)のデータが足りないのである。そのため、モザイク画像のようになってしまったのである。
本来、抽出する走査線の数は、カメラの回転速度に応じて増やしてやらなければならないわけであるが、それが上手く合っていなかったのである。また、今回の画像を見て頂くと判ると思うが、動画ファイル自体も、実は一秒辺りのフレーム数が間引かれたものとなっている。それにより、抽出する走査線の数が一本ではますます足りなくなってしまっていたのである。
というわけで、今回は「失敗した」と言わざるをえない。何か、前回は「簡単である」などと言い切ったような気もするが、それはきっと気のせいであろう。
やはり、これは適当にあるもので間に合わせ仕事をしようとしたせいかもしれない。いつの日か「mov2panorama.exe」を作成し、必ずや必ずや再挑戦をするつもりである(Macでやるのは少しあきらめモード)。
2000-05-17[n年前へ]
■恋の形を見た人は 
恋の相対性理論
さて、前回
では、三人の登場人物A子 : 「瞬間」的に燃え上がるタイプの女の人達の間で繰りひろげられる色々な「出来事・きっかけ」と、それにより発生する「恋する心」を「恋のインパルス応答」を用いて計算してみた。その結果、C男とB子がカップルになれば「ほのぼの」とした幸せな生活をしそうだ、というところまで考察した。
B子 : 「ゆっくり」燃えるタイプの女の人
C男 : いつも、とっても良い男
今回は、その三人に加えて
- D男 : ほとんどの場合、悪い男
さて、今回登場する「D男 = ほとんどの場合、悪い男」はかなり酷い男である。D男がA子とB子に対して何をしたか時系列を追ってみてみることにしよう。
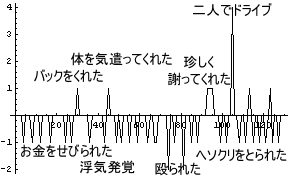 |
- お金をせびり、
- 浮気をするし、
- それを追求すると殴る蹴るの暴行を働き、
- せっせと貯めたヘソクリを奪いパチンコに行ってしまう、
それに対して、前回のC男は次のグラフのように悪いことは何一つしない良い男だ。
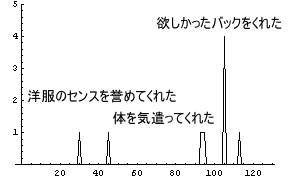 |
悪いことは何一つしない。良いことばかりをしてくれるのである。何とも良い人である。普通に考えれば、女の人の「ハート」はC男ががっちり掴み、D男は警察官にでもがっちり掴まれているのが当然であろう。掴まれたが最後、シャバには二度と出てきてこないで欲しい位である。しかし、そう単純な話ではないのだ。
人の感覚には「順応」というものがある。簡単に言えば「慣れ」である。ひどいことしかしない男と普段接していると、それが当たり前に思えてしまうのである。相対化してしまうのだ。普段のD男に対する印象が「当たり前」に思えてしまうのである。
さて、その「恋する心」の「順応」を計算するにはどうしたら良いだろうか?そう、普段の印象を基準にすれば良いのだ。普段の印象、すなわち「印象の平均値」を「恋する心」から引けば良いのである。例えば、A子のC男に対する「恋する心」を計算してみることにする。次のグラフで黒字が「色々な出来事」と「恋のインパルス応答」の畳み込みであり、本来のあるべき「恋する心」である。そして、緑字が環境順応後、すなわち、本来のあるべき「恋する心」から「印象の平均値」を引いた「恋する心」である。
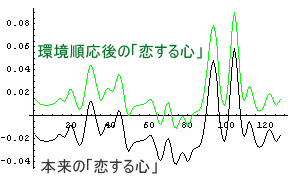 |
この図で、環境順応後の「恋する心」が本来の「恋する心」よりいい印象であることがわかると思う。何故かというと、環境に順応するということは普段の印象が当たり前の状態と思ってしまうことである。普段「悪い」男を相手にする場合は、「悪い」のが当たり前だと思ってしまうのである。数学的には、「悪い」のを引くのであるから、「マイナスを引くとプラスになる」のと同じである。それを式で表してみると、
環境順応後の「恋する心」 = 本来の「恋する心」 - 普段の態度
なのであるから、普段の行動が極めて悪いD男の場合は
環境順応後の「恋する心」 = 本来の「恋する心」 - ( 悪い印象)ここで「悪い印象」が「良い印象」の反対であることから、( 悪い印象 ) =( -良い印象 )とおくと、
環境順応後の「恋する心」 = 本来の「恋する心」 - ( -良い印象)であるから、
環境順応後の「恋する心」 = 本来の「恋する心」 + ( 良い印象)となる。なんと、「悪い印象」が「良い印象」にすり替わるのである。恐るべし、「環境順応」である。スイカに塩をかけると、ショッパイどころか逆に甘く感じられるのと同じく、ひどいD男がちょっとでも良いことをすると、「ものすごく良いこと」に感じられてしまうのである。前回、
「恋の印象の平均化効果」というものを武器に、「辛(つらい)」が「幸(幸せ)」にすりかわる様子を見てみることにしたい。「辛(つらい)」が「幸(幸せ)」は紙一重なのだ。「辛(つらい)」は「幸(幸せ)」で、「幸(幸せ)」は「辛(つらい)」なのである。と書いたが、これがそうだ。普段の「辛(つらい)」を引くと、マイナスをマイナスすることでプラスに変わり、「辛(つらい)」が「幸(幸せ)」にすりかわるのである。
そして、普段悪いことをしないC男の場合はこれとまったく逆に、普段の良い印象を引いてしまうが故に、環境順応後の「恋する心」には「悪い印象」が加わってしまうのである。「普段良い男」が少しでも悪いことをすると、散々に悪く言われてしまうのと同じである。
さて、こういった環境順応した状態での、A子のC男に対する「恋する心」とD男に対する「恋する心」を眺めてみることにしよう。次のグラフは黒字がA子のC男に対する「恋する心」を示し、緑字がA子のD男に対する「恋する心」を示している。
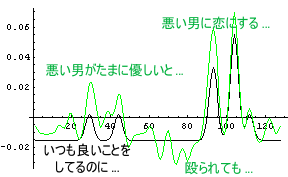 |
なんと、A子は普段悪いD男の方に強い「恋する心」を感じてしまうのである。「おいおい、それでいいのか?」、と言いたくなるような状況である。「オマエはマゾか!?」と、つい言ってしまいそうである。
まぁ、じっくり物を考えないA子はおておいて、それではB子はどうだろうか?きっと、C男と上手くいくだろうB子はどうだろうか?もちろん、「人の良い」C男を選んでくれるだろう。というわけで、次のグラフが、A子とB子のD男に対する「恋する心」を比較したものである。緑字がA子のD男に対する「恋する心」を示し、黒字がB子のそれを示している。
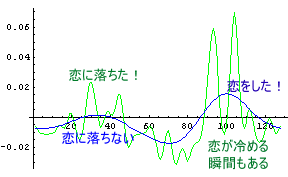 |
何ということだろう。こともあろうに、B子もD男に恋をしてしまうのだ。哀しいかな、C男は失恋してしまうのである。しかも、こtもあろうにD男にである。なんということだ!もちろん、D男がB子にひどいことをした時、すなわち「B子のD男に対する恋する心」が低下した時にA子とD男が別れるという可能性もある。しかし、残念ながらB子は「ゆっくり」タイプなのである。A子と違って、「すごく恋が冷める瞬間」がないのである。A子の場合はとっさのいきおいでD男と別れるという可能性もあるが、B子の場合はむしろD男にひっかかりやすいと言えるかもしれない。
このようにして、「普段は悪い男がたまに優しいことをすると、女の人はふと恋に落ちてしまう」という恐怖のストーリーがいたるところで発生するのである。
私の楽しみ「ちゃろん日記」の2000/03/09の「わしはダメだった」に、「印象の平均化定理」に関するしみじみとした一節があるので、そのまま引用してみたい。
「下僕(仮名)は、不幸な女がどぅやってできるか知っとるか?」「一般相対性理論」によれば、完全なる時空間の基準がない。それと全く同じように、絶対的な幸せの基準など存在しない。本人がそれでいいと言うなら、それでいいのかもしれない。強引を承知で言うならば、それが「恋の相対性理論」である。恋の座標軸は本人が決めるしかないのである。「・・・う?ん」「不幸な女は、フダンはとんでもない男がたま?にほんのすこしだけ見せる優しさが忘れられないコトにより生産される」「・・・・・・」「母ちゃんがそぅだった、こりからもそりは生産されるだろうしそんな女が絶えるコトはないだろう、でもそりでいいのカモ知れんの、本人がそりで幸せだったのなら」
さて、これまで、「できるかな?では何度も「恋のかたち」を何とか目に見える形にしようとしてきた。きっと、それはこれからも変わらないだろう。とりあえず今回の話は、私の好きな本橋馨子の「兼次おじ様シリーズ」の中のセリフを引用して、締めくくることにしたい。
「なぁ兼次、愛はどんな形をしているか知っているか?」
「見た事ないからわかりません。」
「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...」
「もし愛に優劣を決めるものがあればなんだろう?... たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」
2000-05-31[n年前へ]
■あなたのモニタの守備範囲 
ICMファイルを眺めてみよう
ほとんどの場合、私はWEBページはNotePCの画面を見ながら作成する。かといって、WEBを眺めるのもNotePC上が多いかというと、そういうわけではない。眺めることに関しては、CRTディスプレイを眺めるほうが時間からいうと長い、と思う。
そして、NotePCの液晶画面で作成した画像などを、hirax.netのサーバー内にアップロードして、CRTディスプレイ上で眺めると「見た目が全然違ってあせる」ことがしばしばある。私の使っている「NotePCの液晶ディスプレイ」と「CRTディスプレイ」でカラーマッチングが上手くいっていないのである。
上手くいっていないのも当然で、何しろ色の調整なんか(ソフト上では)全然していないのである。もちろん、CRTディスプレイの方は色味やコントラストや何かは結構調整した。しかし、NotePCの液晶の方なんか全然調整はしていない。まして、メインで使っているWindows2000上では調整なんか全然していないのである。
かつて、メインマシンとしてMacintoshを使っていたときには、使うモニタのプロファイルなどを個別調整したりして、結構気を使っていた。しかし、Windowsをメインで使うようになってからはとんと気にしなくなっていた。モニタの色合わせについてはあまり考えていなかったのである。いけない、いけない。これではいけない。「考えないことは罪である」が私のモットーである(今決めた)。
そこで、今回Windows上のディスプレイの色合わせについて調べてみることにした。まずは、画面のプロパティを見てみる。そこには、次の画面のようにどのような色特性のモニタを使っているか設定する画面がある。
 |
この中で、自分の使っているディスプレイに合わせたカラープロファイルを選択してやるといいのだろうか。とりあえず、windowsディレクトリの中には色々な種類のデバイスのカラープロファイルがずらずらとある。例えば、こんな感じである。
 |
拡張子で言うと*.ICMというやつである。ICMはImage Color Matchingの略で、windows内部でカラーマッチングを行う機構のことである。さて、こういうふうに色々ファイルがあるのは判るのだが、これだけでは一体何がなんだか判らない。よく判らないファイルは、中身を除いてみたくなるのが自然だろう。例え、それが透け透け水着であっても、ミニスカートであっても、隠されたものは覗き込みたくなるのが人情である。
そこで、少し情報を調べてみると、
http://labs.nec.co.jp/hide/ICPLIB-listj.html
にicplibという、ICMファイルの読み書きにとっても便利なライブラリーがあった。NEC様が作成されたライブラリーでとても簡単にICMファイルをいじることのできる「とてもありがたい」ソフトウェアである。
適当にこの中を眺めてみると、サンプル中にICMファイルの中身を読み出して、表示するアプリケーションがある。早速、コンパイルしてやると、こんなソフトである。
 |
上の画面のように、試しにICMファイルを読み込んでみる。すると、その中身は次のようなものが書き込まれているのがわかる。これは、sRGBColor Space Profile.icmというファイルの中身の場合である。
 |  |
この中にはずらずらと色々なデータが書き込まれている。一例を挙げると、そのディスプレイの赤の色がXYZ色度座標でどの値か、というようなことが書いてあるのだ。例えば、次の図がそれを示したものである。(X,Y,Z)= (0.436,0.225,0.1392)となっているのが見えると思う。
 |
ここでは赤の座標値だけを眺めたが、Red,Green,Blueの各座標の値を眺めてみれば、そのディスプレイがどんな色空間を表示可能なのかが目安としてわかるだろう。Red,Green,Blueの組み合わせで色を表示するわけであるから、当然その三つの座標で囲まれる三角錐の範囲の領域が表示可能なわけである(大雑把に言えば)。ということは、このICMファイル、カラープロファイルを見れば、それぞれのディスプレイの大雑把な性能が判るわけだ。とても、大雑把にだけど。
それでは、試しに、いくつかのディスプレイを用いて、表示可能な色空間の範囲をICMファイルを頼りに調べて、試しに比較をしてみたいと思う。
さて、どういうディスプレイで比較をするかであるが、ディスプレイと言えば「ナナオ」である。いや、少なくとも一時はディスプレイと言えば「ナナオ」であった。売れすぎた今となってはどうなのかは知らないが、私にとっては川崎和夫がデザインを担当したことがあるということだけで、十分なくらい気になるブランドである(しかし、実は私はナナオを使ったことがない。私は何故かダイアモンドトロン一筋なのだ)。「欲しいけど高い。」 「高いけど欲しい」なのである(高くて買わないけど)。
そういうわけで、気になる「ナナオ」のディスプレイの色特性を見てみることにした。まずは、
- EIZO / JAPAN ( http://www.eizo.co.jp/home/support/sw/)
- CRTディスプレイ
- 液晶ディスプレイ
- プラズマディスプレイ
- EIZO CRTディスプレイ EIZO FlexScan E57T ( E57T__65.ICM )
- EIZO 液晶ディスプレイ EIZO FlexScan E151L ( E151L_M1.ICM )
- EIZO プラズマディスプレイ EIZO FlexScan P4260 ( P4260_M1.ICM )
以前、
- WEBページは会社の顔色 -WEBページの色空間を考える2- (1999.04.26)
- 色を伝える時に、考え忘れていたこと(色弱と色空間 その1) - We can work it out! - (1999.08.09)
- すごく太い線 液晶ディスプレイ EIZO FlexScan E151L
- 中間の太さの線 CRTディスプレイ EIZO FlexScan E57T
- 細い線 EIZO プラズマディスプレイ EIZO FlexScan P4260 ( E151L_M1.ICM )
 |
ハイビジョンテレビといってもCRTなわけである。だから、以前計算したハイビジョンテレビの色空間と「CRTディスプレイ EIZOFlexScan E57T」のそれがかなり近いのは当然である。
それに対して、「液晶ディスプレイ EIZO FlexScan E151L」の色空間はずいぶんと狭い。青方向はかなり狭いし、赤方向に対しても若干狭い。深い青色の海の中で、赤い熱帯魚が群れるような景色を観るのにはもしかしたら向かないのかもしれない。
「プラズマディスプレイ EIZO FlexScan P4260」の場合も、やはり若干青・赤方向が弱い。しかし、何やら緑方向にやたら広い発色可能な領域がある。緑の大草原の画像をこのディスプレイを使って眺めてみたくなる。きっと、結構キレイなのだろう。
さて、今回、少し調べてみたicmファイル(カラープロファイルファイル)には、それぞれのディスプレイの出せる「色空間」が書かれている。言わば、それぞれのディスプレイの「守備範囲」が書かれているわけだ。それぞれのディスプレイにそれぞれの「守備範囲」がある。それぞれのディスプレイやプリンタ達の「ここの範囲ならまかせとけ」という範囲である。
その守備範囲をちゃんと知ってさえいれば、「少ない戦力でも勝つこと」ができるかもしれない。また逆に、その守備範囲を間違えるととんでもないことになる。「勝てる試合も負けてしまう」し、「ケガでリタイアする選手も出」てきてしまう。江本猛であれば、「ベンチがアホやから野球をやってられん」という名言を言うところだろう。
というわけで、ディスプレイ達にそう言われないようにするためにも、カラープロファイルファイルでこれからも遊んでみたい、と思う。
また、「カラープロファイルで眺める各社のプリンターの性能比較」というような企画でもしてみようかな、とふと思うのであった。
2000-11-07[n年前へ]
■SEXYタレント売り出し術 
または恋のフライバイ
朝のテレビと言えばテレビ朝日の「やじうまワイド」である。私はニヒルな吉澤アナウンサーが大好きなので、毎朝TVのチャンネルを「やじうまワイド」に合わせておくのが日課なのである。
吉澤アナの素晴らしさを少し語らせてもらえば、コメンテーターが変なコメントを言った場合、吉澤アナは即座に「本当にそうですかねぇ?」といとも簡単に否定する。しかも、深夜番組ではなく、早朝のさわやかな時間帯にである。コメンテーターの威厳などあったものでない。しかし、コメンテーターの威厳というモノがそんな言葉で否定されるようなならば、そんなものは実は「張りぼて」のような威厳であるわけで、その張りぼてを日の下にさらしてしまうそのイケズな感じが私は実に大好きなのだ(そしてそんな斜に構えた吉澤アナがホントーにたまに真剣な目になる感じが私は同時に大好きだ)。
とりあえず、そんな感じで毎朝「やじうまワイド」を流していると、梨本勝とか福岡翼などの芸能レポーター達が芸能スキャンダルをしゃべりまくり、いやでもそれらが耳に入ってくるのである。朝のTVはと言えば、何はなくともまずは芸能スキャンダルなのだ。といっても、私の耳は興味のないことにはかなりの難聴気味になるらしく、それらの芸能スキャンダルは耳には入ってくるのだが残念ながら頭には入ってこない。
そんな私でも、芸能オンチの私でもスキャンダルを利用した「SEXYタレントの売名行為」が多いことには驚いてしまう。古くは(そんなに古くない?)「古屋一行のAVギャルスキャンダル」から、「羽賀研二と桜庭あつこ」や「岡村隆史と美人巨乳釘師」まで、そんな話は腐るほどある。
確かにそんな話は腐るほどあるのだが、SEXYタレント売り出し術を科学的に考察したという話は今だ聞いたことがない。私が不勉強なせいかもしれないが、少なくとも私は聞いたことがない。
一体、それはナゼだろうか?ミョーに科学的な芸能プロダクションあたりが、そんな研究をしないものなのだろうか?もうすぐ21世紀になるというのに、そんな科学的な芸能プロダクションは存在しないものなのだろうか?
いやもちろん、そんな芸能プロダクションはないだろうし、そんなクダラナイことも誰もあえてするわけもないだろう。しかし、クダラナくて誰もそんなことをしないというのであれば、それはもう本サイトの大好きなジャンルである。というわけで、今回は「SEXYタレントの売り出し術」を考察してみることにした。
まず、芸能に疎い私が考えてみるに、なぜかだか知らないが「SEXYタレントの売り出し術」は「愛」を装うのが普通である。「古屋一行のAVギャル」でも、「羽賀研二と桜庭あつこ」でも、「岡村隆史と美人巨乳釘師」でもいずれも「始まりはいつも愛」なのである。こう書くと「ちょっといい話」に聞こえるが、実は全然「いい話」ではないのが不思議と言えば不思議であるが、とりあえず「SEXYタレントの売り出し術」は「愛」の一応用例として考えることができるかもしれないわけだ。
本WEBサイト「できるかな?」でも「愛」ならぬ「恋」の力学は常日頃から考えているわけで、「恋の力学」が解けるなら、「愛の力学」も解けるかもしれないし、だとしたら、「SEXYタレントの売り出し術」も解けると言っても必ずしもウソとは言えないだろう(典型的な詭弁)。そこで、今回はこれまで考えてきた「恋の力学」を応用することで、「SEXYタレントの売り出し術」を考えてみることにした。
とりあえず、登場人物として次のような三人を考えてみよう。
- 登場人物 男性タレントA : 名実共にA級のタレント。
- 登場人物 男性タレントB : B級タレント。沖縄に店を経営していたりする。女性に「誠意」を見せるのが得意中の得意。
- 登場人物 女性タレントC : C級タレント。少なくとも私には「誰だそれ」状態の無名人。だけど、大抵の場合SEXY度だけはバツグン。
つまり、
- 女性タレントCがはるか遠くから男性タレントAに近づいていく
- 女性タレントCと男性タレントAが最接近する
- 女性タレントCが男性タレントAから離れ、ずっと離れた方に行ってしまう
- 女性タレントC
- 男性タレントA
しかも、男性タレントAの存在感と女性タレントCの存在感はあまりに差がある。そのため、女性タレントCが近づいてきても男性タレントAはビクともしない。もちろん、もともと男性タレントA自身は芸能界の中をどっしりと動いているわけであるが、女性タレントCが近づいてきても我関せずである。それに対して、女性タレントCは男性タレントAに近づくことで影響を受ける。
このような場合は単純なケプラー運動の一例であり、細かい導出はメンドくさい(私が)のでしないが、女性タレントCは男性タレントAの近くでは、彼を基準とした座標系で双曲線軌道を描く。普通であれば「双曲線軌道」という言葉には何の色っぽさもないが、コトが「SEXYタレントの売り出し術」であるだけに、双曲線軌道という言葉でさえ何か色っぽさを感じてしまうのは私だけだろうか?
そんなことはおいておいて、女性タレントCは男性タレントAに近づいて、そして離れていくのである。その時、彼女は彼を基準とした座標系で双曲線軌道を描くわけだ。
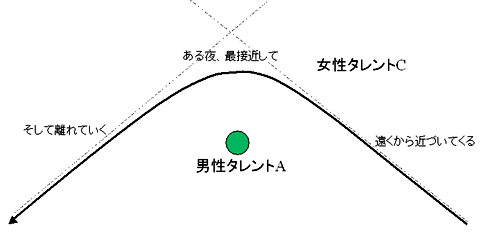 |
この場合、女性タレントCの「イキオイ」(ここでは速度とでもしておこう)は男性タレントAを基準とした座標系では「一番最初に近づいてくる時」と「一最後に離れて行く時」では変わらない。もちろん、方向は違うのだが、大きさは同じである。それを描いてみたのが次の図である。女性タレントCのイキオイは最初と最後では、方向が違うだけで大きさは同じコトがわかるだろう。
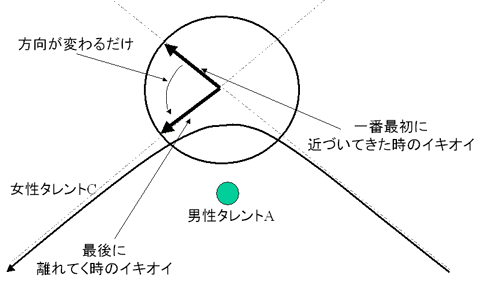 |
この場合、「SEXYタレントの売り出し術」としては単に女性タレントCの方向転換を図っただけ、である。図に書くとこんな感じだ。
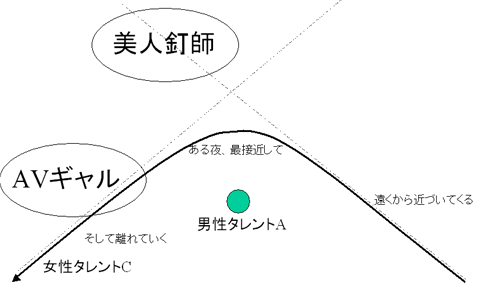 |
ちょっと具体的すぎたような気もするが、この例はフィクションにすぎない。別に男性タレントAがナイナイ岡村だと言っているわけではない、と一言だけフォロ〜しておくことにしよう。
さて、この場合の「SEXYタレントの売り出し術」はかなり低レベルなテクニックである。これは単に女性タレントCの方向転換ができただけである。それ以外のさしたる効果は何もない。
しかし、これまで考えてきた「恋の力学」を応用して考えるに、さらなる高度な「SEXYタレントの売り出し術」が考えられる。それはどのようなテクニックかと言えば、相手すなわち男性タレントAのイキオイを利用するのである。日本のお家芸の柔道のように、相手の力を利用してそれを自分のモノとするのである。
こちらは、結構ハイテクニックなので判りにくいが、それをなんとか絵にしてみたのが次の図である。この場合、「男性タレント自身にもともとイキオイがある」ことが重要である。すなわち一般視聴者を基準とした座標系に対して、男性タレントA基準系は動いているのである。
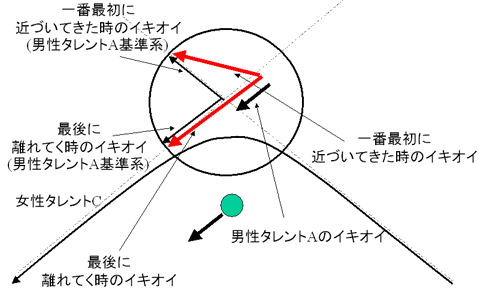 |
すると、一般視聴者を基準とした座標系では、面白いことに女性タレントのイキオイ自体も男性タレントに接近する前と後で変わるのである。もちろん、上の図を見てもらうと判るように、男性タレントA基準系では女性タレントのイキオイは方向が違うだけで、大きさはなんら変わっていない。しかし、それは男性タレントA自身がイキオイがあるためで、一般視聴者を基準とした座標系では女性タレントCのイキオイは増しているのである。赤い線で描いた「一般視聴者を基準とした座標系での女性タレントCのイキオイ」が最初と最後で違っているのが判るだろう。つまり、女性タレントCはこの接近戦でイキオイが増しているわけだ。これが比較的高度な「SEXYタレントの売り出し術」である。このテクニックを使えば、男性タレントの背後から近づけば女性タレントCのイキオイは必ず増すということになる。
さて、それでは女性タレントCの接近相手が
- 男性タレントB : B級タレント。沖縄に店を経営していたりする。女性に「誠意」を見せるのが得意中の得意。
そして男性タレントB相手の場合には、もうひとつ問題がある。相手が名実共にA級のタレントAであると、タレントAは女性タレントCが近づいたくらいではビクともしない。しかし、それがタレントBの場合だと、あまりに重みがないために女性タレントCがタレントBに近づくと揺れ動いてしまうのである。そんな状態では「SEXYタレントの方向転換」すら上手く行くかどうか判ったものではない。誠意大将軍の彼を頭に浮かべて頂ければ、おそらく納得して頂けると思う。
さて、今回は相手の力を利用して自分のイキオイを増す「SEXYタレントの売り出し術」方法を考えてみた。もちろん知っている人も多いだろうが、これはフライバイ(flyby)とかスイングバイ(swingby)と呼ばれるテクニックで、ロケットの軌道制御などに使われるテクニックだ。それを「SEXYタレントの売り出し術」に応用してみたわけだ。
最初の方に書いたとおり、今回は「SEXYタレントの売り出し術」は「愛」の一応用例として考えてみたのだから、このフライバイを「恋・愛」に適用してみるのも面白いのではないだろうか?例えば、あなたが誰かに恋をして、その恋をすることで自分自身も輝いたりイキオイが生まれることがあるはずだ。このフライバイを行う限りは、相手とはすれ違うだけで、いずれ遠くへ離れてかざるをえないわけであるが、少なくともその「恋・愛」であなたが成長することもあるだろう。相手の後ろから追いかけて、そして少し方向を変えてまた離れていくときに、イキオイは必ず増すだろう。それは一つのフライバイ、「恋・愛」のフライバイと言っても良いのではないだろうか、と思ったりするのである。もちろん「SEXYタレントの売り出し術」と同じで、それは結局相手次第だと思うけどね。
2000-11-26[n年前へ]
■ブランコの中の∞(無限大) 
なんで一体漕げるのだろう?
公園のブランコというのは、何故かとても不思議な雰囲気を持っている。ホントにうるさいくてたまらないくらいのガキんちょ達が、アクロバットのようなスゴイ技を見せていたりする。それは、まるで上海雑伎団を見ているような気分になる。小さな子がなかなかブランコが漕げず、ブランコの上で宇宙遊泳のように四苦八苦しているのを見ているのも思わず笑ってしまうくらいに可愛らしいものだ。もちろん、そこは子供の領分というだけではなくて、黒沢明の「生きる」の主人公がしていたように「大人がブランコに座って揺れていたり」すると、思わずその人の陰に隠れている物語を想像したりしてしまう。ブランコの周りというのはそんな不思議な雰囲気を持っているのだ。
やたらにブランコを漕ぐのが上手いガキんちょもいる一方で、全然ブランコを漕げず四苦八苦する子供もいる。ブランコを漕ぐコツを覚えるのもなかなか大変そうである。考えてみれば、ブランコは一体どういう風に漕ぐものなのだろう?口で上手く説明できる人がいるだろうか?
それに、そもそも私たちはブランコを何故漕ぐことができているのだろう?
いったい、いつから疑問に思うことをやめてしまったのでしょうか? いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか?という手紙で始まるのは加納朋子の「ななつのこ」だが、「何故、リンゴは落ちるのかという謎」と同じく、「ブランコの漕ぎ方の謎」だってとても不思議だ。いつも目にする公園のブランコを、私たちは一体どうやって漕ぐことができているのだろう?
いつだって、どこでだって、謎はすぐ近くにあったのです。
何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。
もちろん、「何でブランコの漕ぎ方が不思議なのさ?」と言う人も多いだろう。その中には理路整然とブランコの漕ぎ方を説明してくれる人もいるだろう。そして、「特にブランコの漕ぎ方をじっくり考えたことなんかないもんね」という人も多いに違いない(私だけかもしれないが)。そこで、まずは「ブランコの不思議」を簡単に書いてみることにしよう。
次の図は「ブランコを漕いでる子供」である。
 |
この子供が何もせず立っているだけ(あるいは座っているだけ)だったら、どうなるだろうか?それはもちろん、単なる振り子と同じくようにブランコは動く。もしも色々な摩擦がなければ、まったく同じように動き続けるだけだし、摩擦力があればブランコの動きはただ減衰していくだけである。つまり、子供が何もしなければ、ブランコの動きは「遅く・小さく」なることはあっても、ブランコが「速く・大きく」なることはないのである。
だからブランコを速くするためには、「ブランコに乗ってる子供がブランコを漕がなければならない」わけであるが、ブランコに乗ってる子供は一体どんなことができるだろうか?
次に示す図は「ブランコに乗ってる子供を中心にとった座標軸」を描いてみたものだ。この図の中で直交する二つの軸を描いてある。つまり、
- ブランコの動きの中心を向いている軸A
- 軸Aに直交する、つまりブランコの進行方向(あるいはその逆方向)を向いている軸B
 |
ところが、実は「ブランコに乗ってる子供」はこの二つの軸の内の片方、軸Aに対しての動きしかできない。何故なら、軸B方向に対しては「ブランコに乗ってる子供」動きの支えになるモノが全然無い。だから、ツルツル滑る氷の上では全然動けないのと同じく、「ブランコに乗ってる子供」はその方向には動けないのである。もし子供がその方向に動こうとして体を動かしたりしても、結局子供の重心はその方向には全然動かないのだ。
それに対して、ブランコの動きの中心を向いている軸A方向に対してはブランコの鎖も座っている(あるいは立っている)板が支えになるわけで、その方向に対しては「ブランコに乗ってる子供」は動くことができる。
というわけで、ブランコの上では「ブランコの動きの中心を向いている軸A」方向にしか動けないわけであるが、その方向というのはブランコの進行方向に対しては直交している。つまり、ブランコを漕ぐためには、「ブランコの進行方向に対して直交している方向に動く」しかないことになる。
ここまで書くと、ブランコの不思議が判るハズだ。ブランコを漕ぐ、つまりブランコを軸B方向の速度を上げたいのに、我々は「軸Bに対して直交している方向に動く」ことしかできないのである。一体何故、軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増すのだろうか? この謎「ブランコの不思議」を、ゆっくり考えてみることにしよう。
まずは、ブランコに乗ってる子供が立ち上がったりして、「ブランコの動きの中心を向いている軸A」方向に動いた場合、何が起きるだろうか?
 |
「ブランコの動きの中心を向いている軸A」方向に動くと、ブランコの鎖の長さが短くなることと同じである。すると、回転しているブランコの鎖が短くなるわけで、そうするとブランコの速度は速くなる。何故なら、角運動量が保存されるからである。ちょうど、スケートのフィギア競技の選手が回転中に伸ばしていた手を縮めると回転数が早くなるのと同じだ。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの半分だけ(とんでもない身長の子供だ!)上がれば、ブランコの速度はもとの速度の倍になるのである!
ということは、少なくともこの瞬間は「軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増す」わけであるが、これでブランコの漕ぎ方を納得するにはまだまだ早いのである。確かに、「ブランコの動きの中心を向いている軸A方向に動く」とブランコの速度は増すわけであるが、それはその瞬間だけである。ブランコの上で「立ち上がり続ける」なんてことはできないわけで、速度が増し続けるわけではないのである。
もしも、「もう一度ブランコの上で立ち上がるために、すぐに低い姿勢に一旦戻ったり」したら大変だ。ブランコの鎖の長さが長くなるのだから、今度はブランコの速度は遅くなってしまうのである。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの二倍だけ(つまりさっき立ち上がった逆の動きである)下がれば、ブランコの速度はもとの速度の1/2になってしまうのだ!
これでは、結局さっきの速度が二倍になったことは帳消しになってしまう。つまり、「単純に」角運動量の保存を考えるだけではブランコの速度を(長い間にわたって)早くしていくことはできないわけだ。
このままでは、「ブランコを漕ぐことなんか不可能である」という結論が出てしまいそうになるが、ブランコを漕いでる子供達はイッパイいるわけで、そんな結論を受け入れるわけにはいかない。彼らがみんな超能力でブランコを漕いでいるわけもないのである。まだまだ見落としていることがあるので、ブランコの不思議の謎が解けないだけのハズなのだ。
そこで、ちょっと考えてみると「とんでもなく単純なこと」を見落としていたことに気付いた。それは、「タイミング」である。例えば、ブランコの速度がずっと同じであるすると、
- 初期のブランコの速度 = 10
- 重心位置を高くして 10 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- 重心位置を低くして 10 X 1/2 = 10 (何てこったい、速度が半分になっちまったか!)
- 初期のブランコの速度 = 10
- 重心位置を高くして 0 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- そのあとブランコの速度 = 0
- 重心位置を低くして 0 X 1/2 = 0 (0が0になっても全然変わってないもんね!ヘヘン!)
人生何事もタイミングが重要である。失恋した男性や女性にタイミングをわきまえた「恋のハイエナ」達が寄ってくるのと同じく、またお金に困っていると何故かサラ金の広告が目の前にチラチラするのと同じく、ブランコを漕ぐにはやはりタイミングが重要なのだ。
なるほど、考えがまとまってきた。このイキオイでそのまま「ブランコの理想の漕ぎ方」まで考えてしまおう。
まず、「重心位置を高くしてブランコの速度早くする」にはできるだけ速度が速い瞬間に行うのが良いだろう。倍率が確定している賭なのだから、元金はあればあるほどおトクである。1万円×2=二万円では1万円しかもうからないが、一千万円×2=二千万円では一千万ももうかるのだ。ブランコの速度が速い瞬間に立ち上がれば、一番おトクに速度を増すことができるのである。
もちろん、ブランコの速度が速い瞬間といえば、明らかにブランコが一番下にきた瞬間である。つまり、ブランコが一番下にきた瞬間に立ち上がれば「一番おトクに速度を増すことができる」わけだ。しかも、その瞬間は鉛直に重心を持ち上げることになる。つまり、位置エネルギーを効果的に増加させることができるわけだ。結局、この時に増加させた位置エネルギーは後で、運動エネルギーに変換されるわけで、結局これがブランコの運動の源となるのである。
そして、「次にもう一度立ち上がるために一旦低い姿勢に戻る瞬間」=「速度が遅くなる瞬間」はブランコが停止しているときであれば何の問題もない。ブランコはもともと止まっているんだから、その速度が何分の一になったって全然気にしないもんね!となるわけだ。そのタイミング= ブランコが止まる瞬間といえば、もちろんブランコが最高地点まで上がった瞬間である。つまり、ブランコが一番上にいった瞬間に低い姿勢に戻れば全く減速無しに次の加速に備えることができるわけである。しかも、その時には実は運動エネルギーを位置エネルギーに変えることで、隠し財産にしているわけで、もう汚い政治家のマネーロンダリングのような見事な方法なわけだ。
というわけで、
- ブランコが下に来たときに(立ってる場合は)足を伸ばして立ち上がったり、(座ってる場合は)足を曲げたりすることにより高い位置に重心を持ってきて(しかも、重力に逆らって重心を上げるため位置エネルギーが増加する)
- ブランコが上に行ったときにその姿勢を元に戻す
それでは、確認のためにそのやり方で本当にブランコが漕げるのかどうか、シミュレーション計算を行ってみた。ブランコの動きは振り子運動だが、振れ幅がとても大きいので、cosx≒xというような近似をする単振動としての扱いはできない。そこで、楕円積分の計算を行わなければならない。が、私が自分の力でできるかどうかはともかく、そこはMathematicaに解かせればイッパツである。もう、驚くくらい簡単なのである。自分の力で解いていないところが、実に悲しい現実ではあるが、それが現実なのだからしょうがない。
というわけで、ブランコの動きのシミュレーションをしてみた結果が次のグラフである。「ブランコに乗ってる子供」の漕ぎ方としては、以下の三つ
- 何もしない場合
- ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合
- ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合
 → ブランコの動きはず〜と変わらない |
ブランコが上にきたあたりで座り込んだ場合  → ブランコの動きはどんどん大きくなる 「やったぜ、これが理想の漕ぎ方だぁ。」 |
ブランコが上にきたあたりで立ち上がった場合  → ブランコの動きはどんどん小さくなる 「なんてこったい、遅くなっちまったぁ。」 |
この結果から、ちゃんと1.の「何もしない場合」は「ブランコの動きはず〜と変わらない」し、理想の漕ぎ方であるハズの2.の「ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合」は「ブランコの動きはどんどん大きくなる」し、最悪の漕ぎ方であるハズの3.の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合」には「ブランコの動きは逆にどんどん小さくなってしまう」ことがわかる。というわけで、今回考えた「ブランコの不思議= 漕ぎ方」はシミュレーション計算結果からも確かめることができたわけだ。
ところで、こういったタイミングを考えながらパラメーターを変えることで動きを大きくしたりすることは「パラメータ励振」と呼ばれる。ブランコの漕ぎ方はその「パラメータ励振」の応用のひとつである。「何故、リンゴは落ちるのかという謎」には重力という基本的な物理現象が隠されていたが、それと同じく、「ブランコの漕ぎ方の謎」にも「パラメータ励振」という物理現象が隠されているのだ。次回以降も、この「パラメータ励振」を手がかりにいくつかの「身近な謎」に迫ってみたい、と思うのである。
さて、公園でブランコを漕ぎまくる子供をもし見かけたならば、ぜひ横から子供の動きを見てやってもらいたい。きっと、その揺れ動くブランコの中にはこんな∞(無限大)の形が見えるハズだ。天まで上ろうとする「ブランコの秘密」はその「ブランコの中の∞(無限大)」に隠されていたのである。子供も含めて人間の可能性は∞(無限大)だと私は思うが、ブランコの揺れる動きから、そんなことを考えてみるのも少し面白いのではないだろうか? それとも、ちょっと考え過ぎかな。

