1999-08-08[n年前へ]
■瞳の中の真実 
目の屈折率を調べよう
先日、近所の海へ行ってきた。水中メガネで覗いているとまるで熱帯魚みたいな魚が泳いでいて素敵なのだ。水中メガネを使うか使わないかで、海の楽しさは雲泥の差である。水中メガネで覗いてみると、裸眼の時とは別世界のようにくっきり見えるのである。
 |
さて、「水中視の光学」と言えば、物理の散歩道の「アユと泳ぐ」(新物理の散歩道-第2集- 中央公論社)に詳しく面白い考察がされている。本WEBでもScrapsにて「焦点」ということを考えたばかりなので、「アユと泳ぐ」と同様の解析を「できるかな?」風に行ってみたい。光学シミュレーターを作ってみたいのである。そのために、まずは人間の目の中の屈折率を調べなければならないだろう。というわけで、今回は下調べ編である。
それでは、人間の左目の水平方向の断面図を調べてみる。
 |
この中で普通のカメラでいうレンズの役割を果たしているのはどこだろうか。レンズの部分を赤く塗るとどのようになるだろうか?下に並べた3つのうちどれだと思われるだろうか。
A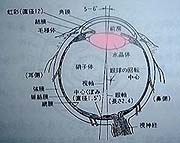 | B | C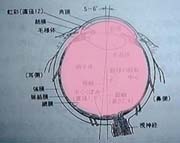 |
まずは、目の中の物質の屈折率を調べてみると、以下のようになる。
| 場所 | 屈折率 |
| 角膜 | 1.376 |
| 眼房 | 1.336 |
| 水晶体 | 1.386 |
| 硝子体 | 1.336 |
空気(15℃の乾燥空気)の屈折率はほぼ1.0であるから、空気と比較するならば、目の中の物質はほぼ同じ屈折率を持つといっても良い。角膜も眼房も水晶体も硝子体も同じ屈折率を持つとして良いだろう。すなわち、大雑把な近似においては図.2のCに示したようなピンク色のレンズがあるとして良い。つまり、目全体がレンズであり、レンズ面に焦点を結ぶようになっているのである。水晶体は若干の補正を行うに過ぎない。レンズの焦点はレンズから離れた場所にあるはずと思っている人もいるかもしれないが、レンズの表面に焦点があるものも実はよく使われている。
さて、人間が水の中に入るとどうなるだろうか?水は1.333(589.3nmの波長の光に対して)の屈折率を持つ。これは人間の目の中の物質の屈折率とほぼ同じである。水を主体として出来ている人間なのだからこれは当然だろう。しかしこれでは、目は光を屈折させることはほとんどできなくなる。そのため、水の中に入るときには水中メガネなどで目の回りを空気で満たしてやることが必要なのである。
本題からははずれるが、資料を眺めていると、面白いグラフが目に入ってきた。人間の目の断面方向の視細胞個数の分布を示したものであり、錐体と桿体を個別に示してある。「盲点」なんかも図中にある。
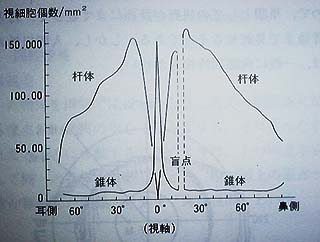 |
目に映る明るさって何ですか? - 君は天然色 - (1999.07.05)
の回に錐体と桿体については触れたが、桿体は1lx程度の暗さから働き、明るさのみに反応する。一方、錐体は10lx以上で働く。従って暗いものを見るには桿体の働きが重要になるわけだが、上のグラフは桿体が視点の中心にはほとんど存在していないことを示している。
従って、暗い所でものを見る際には、視点の中心では感度が足りなくなりやすいことがわかる。これまで、暗い星を眺めるときに視界の中心で見ようとすると見えないのだが、少し視点をずらしてやると見えるような気がしていたのだが、それは気のせいでは無かったようである。
さてさて、資料集めも終わったので「瞳シミュレーションソフトウェア」の開発に着手したいと思う。もちろん、時間がかかるのはいつものことだ。すぐにはできないけどね。
1999-09-26[n年前へ]
■デバイスドライバーは仮免 
ClearTypeの秘密
昨年、COMDEX/Fall '98においてMicrosoftが発表した「ClearType」技術というものがある。液晶ディスプレイなどの表示の解像度をソフトウェアのみで向上させるという技術である。PCだけでなく、液晶を使った電子ブックなどをターゲットにしているという。(参照:http://www.zdnet.co.jp/news/9811/16/gates.html)
技術の詳細については、「特許申請中」ということで、明らかにされていない。しかし、その技術について推論している人は数多くいる。例えば、
- Optimising LCD display of text( http://oxy.sfx.co.nz/lcdtype/ )
- The Technology of Sub-Pixel FontRendering ( http://grc.com/cleartype.htm )
 |
ビックリすることに、確かに効果があるのである。カラーシフティングによりシャッキリした文字になるのだ。しかも滑らかなのである。デジタル接続の液晶を用いている方は確認すると面白いと思う。
もっとも、こういう画像はWEB上で納得するのは難しい。JPEGのような圧縮画像では、情報が完全には保存されず、意図した出力ができないからである。とりあえず、デジタル接続の液晶ディスプレイを使っている方はとにかく試してみると良い。目からウロコである。
さて、この原理であるが、カラーシフトについては色々なところで説明してあるが、若干わかりにくい画像例が多い。そこで、自分流に解釈しなおして考えてみたい。そして、実験してみようと思う。
まずは、右上から左下に走る黒字に白斜線を考えてみる。1ドット幅で、しかも、上から下へ行く間に1ドット右から左にずれるようなものである。液晶の1ドットはRGBが縦に並んでいる。例えば、
で計測した画像例だと、 |
1ドット幅で、しかも、上から下へ行く間に1ドット右から左にずれる黒字に白い斜線を考えてみる。これはそのような斜線を拡大したものである。
そのような斜線を液晶で描くと通常は下の左図のようになる。通常の処理が左で、カラーシフトを用いた処理が右である。通常の処理ではRGBの位置を同じものとして処理しているので、RGBそれぞれが同じように変化している。しかし、カラーシフトを用いた処理においては、RGBの各位置が異なっていることを考慮の上、処理を行ってみたものである。そのため、滑らかな斜線になっているのがわかると思う。
このように、デバイスの個性を把握した上できちんと生かしてやれば、デバイスの能力をもっと引き出すことができるわけだ。 個性の違いを越える世界というのは、個性を無視した世界とはまったく逆であり、個性を最大限理解して初めて個性の違いを超えることができるのだ。
さて、効果を確認するために、そのようなハーフトーンパターンを作成してみた。ただし、ここで表示している画像はJPEGに変換してしまっているので、効果は現れない。また、本来見えるはずの画像とはかなり異なってしまっているので、各画像をクリックしてオリジナルのTIFファイルをダウンロードして確認して欲しい。
 |  |
さて、この画像ではわからないだろうが、TIFFファイルの方を見て頂くと、カラーシフトを用いた斜線ハーフトーンの方では、色模様が出現してしまっているのがわかると思う。それは、液晶のガンマ特性を考慮していないからである。
このガンマ補正については、一般的に使われるガンマの意味だけでないものが含まれている。一言では簡単には説明しきれないので、説明は次の機会にする。Free&Crearでもそのガンマ特性を調整する機能がついている。白地に黒文字であるか、黒字に白文字であるかの違いがあることに注意すれば、その数字の意味がわかる。ここでは、その補正をしたものを示すだけにしておく。と、いっても、私が使用している液晶のガンマを考慮したものなので、一般的には役に立たないだろう。
 |  |
あなたが目にしている画像では、画像ではガンマ補正した方が変に見えていると思う。それは、私とあなたの使っているデバイス(と視点)が異なるからである。ここでやったのと同じやり方で、あなたの液晶に合わせて(なおかつ、同じ視点で)やれば、きれいに出るはずだ。
さて、この結果を私の液晶で見てみると、カラーシフトを用いた斜線(ガンマ補正後)の方ではきれいに斜線のハーフトーンが出ている。ただ、いくつか問題があるのだが、それは次回までの宿題だ。と、いってもヒントはすでに「できるかな?」中でも出現している。ごく最近の話題でも、だ。
このカラーシフト技術は実に単純なアイデアである。しかし、これは実に面白いアイデアであると思う。効果が有る無しに関わらず、こういうネタは私は大好きである。ただ、こういう技術が日本のデバイス屋さんから出てこないことが少し残念だとは思う。デバイスもドライバーも両方作っているところにがんばって欲しいものだ。それまでは、「デバイスドライバーは仮免」といった所だろう。 .....うーん、ちょっと、強引かな。というわけで、何故か私の手元にはPalm-size PCであるCasio E-500があり、そして、久しぶりにVisualStudioをいじり始めるのであった。。
1999-10-15[n年前へ]
■続々ACIIアートの秘密 
階調変換 その2
前々回の
の時にASCIIアートに関する情報を探した- 清竹's テキスト絵 HPリンク集 (http://www2.nkansai.ne.jp/users/kiyo/ )
「限られた出力階調を有効に利用するため、画像の濃度ヒストグラムの補正を行ないます。1パス目で、濃度ヒストグラムをカウントし、そこからヒストグラムが平坦になるような濃度変換関数を生成します。(ヒストグラムを平坦にするのは、情報のエントロピーをなるべく保存するためです。)」とある。Q02TEXTはimage2asciiと同様のテキストアート作成プログラムである。前回のの最後で(3).情報量を最大にするモデル というのを導入したが、これがそのエントロピー最大化アルゴリズムに近いものを導入してみたものである。何しろ、この考えを使っていくのは乏しい階調性の出力機器には非常に有効なのだ。今回は、この「エントロピー最大化アルゴリズム」について考えてみたい。
Q02TEXTは「 .:|/(%YVO8D@0#$」の16階調を使用するテキストアート作成プログラムである。それに対して、「ASCIIアートの秘密」で作成したimage2asciiが使用可能な階調数は一定ではない。指定されたフォントを一旦出力してみて、その結果を計測することにより、出力可能な階調数を決定している。したがって、指定したフォントでしか階調の確かさは保証されない。その代わりに、指定されたフォントを使えば割に豊かな階調性を使用できることになる。
また、得られる階調は一般的に滑らかではないので、Q02TEXTが使っているアルゴリズムとは少し違うものを導入している。
通常ASCIIアートは色々な環境で見ることができるのがメリットの一つである。しかし、image2asciiはフォントを限定してしまっている。これは、目的が通常のASCIIアートとは異なるからである。私がimage2asciiを作った目的は、それを仮想的な出力デバイスとしてみたいからである。その出力で生じる様々な問題を調べたり、解決してみたいのである。
さて、前回の最後に示した3種類の画像変換は
- 単純な階調重視モデル
- オリジナルの0を出力画像の最小値に
- オリジナルの255を出力画像の最大値にする
- 拡大した単純な階調重視モデル
- オリジナルの最小値を出力画像の最小値に
- オリジナルの最大値を出力画像の最大値にする
- 情報量を最大にするモデル
- エントロピーを最大にするための階調変換を行う
これら3つの変換方法の違いにより出力画像にどのような違いが生じていたかを、まずはもう一度見てみる。まずは、オリジナル画像である。これは、「私の尊敬する」S大先生である。私は尊敬とともに「ロボコップSさん」あるいは、「ロボSさん」と呼ぶのだ。いや、本当に。
 |
以下にオリジナル画像及びimage2asciiを用いて変換したものを示す。
 |  |  |  |
- (1).単純な階調重視モデルが比較的白い個所では一番オリジナルに忠実な濃度であることはわかるだろう。ただし、黒い部分に関しての表現力は極めて低い。
- (2).階調性を少しだけ改善したものではそれより視認性が改善している。
- (3).視認度の高い画像ではあるが、オリジナルとは濃度などは異なる?
それでは、これらの画像のヒストグラムを調べてみる。先の「(ヒストグラムを平坦にするのは、情報のエントロピーをなるべく保存するためです。)」というのとの関係を調べたいわけである。
 |  |  |  |
ASCII ARTには濃度の表現領域には限度がある。そのため、(1),(2),(3)はいずれも濃度が最大を示す個所でもオリジナルよりかなり濃度が低い。また、(1),(2)はオリジナルとヒストグラムの形状も少しは「似ている」が、(3)においては、かなり異なっているのがわかると思う。(3)はヒストグラムの形状はかなり異なるにも関わらず、視認度は高くなっている。これが、エントロピーを最大化(すなわち情報量を最大化)しているおかげである。ヒストグラムがかなり平坦になっているのがわかるだろう。
というならば、エントロピーの計算もしなければならないだろう。もちろんエントロピーと言えば、
でも登場している。「エントロピーは増大するのみ...」というフレーズで有名なアレである。情報量を示す値だといっても良いだろう。せっかく、「ハードディスク...」の回で計算をしたのだから、今回もその計算を流用してエントロピーを計算してみたい。といっても、無記憶情報源(Zero-memorySource)モデルに基づけば、ヒストグラムが平坦すなわち各濃度の出現確率が等確率に近いほどエントロピーは高いのが当たり前であるが... この前作成したMathematicaのNotebookを流用するために、オリジナルと3つの変換画像を合体させる。そして、そのヒストグラムを見てみよう。このヒストグラムが非常にわかりにくいと思うので、一応説明しておく。あるY軸の値で水平に1ライン抽出して、その部分のヒストグラムを右のグラフに示しているのである。
 |  |
例えば、オリジナルの画像では髪の毛がある辺り(Y軸で10から30位)では、ヒストグラムを見ればレベルが50位の黒い所が多いところがわかる。それに対して、変換後の画像では、一番濃度の高い所でも150前後であることがわかるだろう。
それでは、それぞれ、Y軸でスライスしてその断面におけるエントロピーを計算したものを次に示してみる。
 |  |
本来は、画像全面におけるエントロピーを計算するのが、望ましい。しかし、ここで使っているような、Y軸でスライスしてその断面におけるエントロピーでも、オリジナルの画像が一番エントロピーが高く、(3)の変換画像(つまり一番上)のものが次にエントロピーが高いのがわかると思う。つまり、情報量が高いのである。
エントロピー量とあなたの感じる「視認度」とが相関があるかどうかは非常に興味があるところだ(私にとって)。エントロピーが多くても(すなわち情報量が多くても)オレはちっともいいと思わないよ、とか、おれは断然エントロピー派だね、とか色々な意見があったらぜひ私まで教えてほしい。
「お遊び」に見えるASCIIアートも、調べていくと実は奥が深いのだなぁ、とつくづく思う。といっても、もちろん本WEBはお遊びである。なかなか、奥までは辿りつかない(し、辿りつけない)と思うが、この「ASCIIアートの秘密」シリーズはまだまだ続くのである。
1999-11-23[n年前へ]
■ミニスカートの幾何学 
32cmの攻防戦
早朝、東名高速で事故渋滞にはまってしまった。仕方がないので、TVを眺めていると、面白い話をやっていた。それは、ミニスカートの丈の話である。何でも、最近の流行はミニスカートの丈が32cmのものであるらしい。女子高生?などが言うには、
「34cmだと長いしぃ。」だから、32cmだと言うのだ。別に、オリンピック選手でもないのだから、ミニスカートの丈の限界まで挑戦しなくても良いだろう、と私などは思ってしまう。しかし、彼女たちはそう考えないらしい。人それぞれである。
「30cmだと下着が見えちゃうしぃ。」
それにしても、スカートの丈が32cmと30cmの間でそんなに、違いがあるものだろうか? 「見える・見えない」を決める分水嶺がその2cmの違いにあるものなのだろうか? 妙に不思議である。 そこで、ミニスカートの幾何学について考えてみることにした。題して「32cmの攻防戦」である。
何より先に確認しておくが、私は今回は科学的好奇心で動いているのである。そこに、一点の不純な気持ちも存在しないことを、ここで確認しておく。いや、むしろ、女性のためのミニスカート理論の構築を目指しているといっても良いかもしれない。といっても、信用されないとは思うのであるが...
 |
さて、先のTV番組によれば、腰からスカートの先までの長さを「スカートの丈」というらしい。また、先のTV番組により、「腰から下着の一番下の部分(股下を計るときの一番上)までの長さが大体25cmである」という重要な情報を得ることができた。
それでは、解析を始めてみよう。以下に、今回考えた「ミニスカートの幾何学」を示す。なお、今回使用する長さの単位は全て(cm )である。
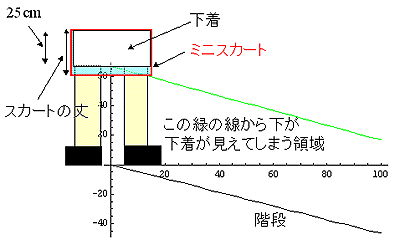 |
まず、階段の途中に立つミニスカートを履いた女性の下着中央部分とミニスカートの最下部を結ぶ直線を考える。この線よりも下が、下着が見えてしまう領域である。もちろん、階段の下には潜り込めないわけであるから、その線と階段で囲まれた領域内から見た際に下着が見えてしまうわけだ。その線のことを「下着防御ライン」と呼ぶことにする。
さて、ミニスカートの形状を考えよう、スカートの丈はもちろん入力条件としてわかる。すると、足りないパラメータは幅である。そこで、ヒップ周りが88cmとしてスカート中央から端までの長さ(rcm)を求める。2πrが88cmであるから、
r = 14cmとなる。
また、駅などの階段というと25度位だろうか。30度というとかなり急な階段である。湘南通商の階段とか急な階段は色々あるが、今回は急な階段の斜度として、25-30度位としておく。ちなみに、京都駅北口のエスカレータで実測したところ、25,6度であった。
それでは、スカートの丈が32cmで階段の角度が30度である場合の計算をしてみる。女性の股下は仮に70cmであるとしておく。おそらく、身長160cm位であれば、この程度であろう。
それでは、ミニスカートの丈が32cm、30cmの時の「下着防御ライン」を計算したものを示す。
 |  |
緑、すなわち、ミニスカートの丈が32cmの時は「下着防御ライン」は階段とほぼ平行である。それに対して、丈が30cmの時の「下着防御ライン」は、ミニスカートを履いた女性から離れるほど階段よりも上に離れていく。ということは、人間の視点位置が「下着防御ライン」を越えるということである。すなわち、下着が見られてしまうということだ。
階段と「下着防御ライン」の差、すなわち、人の目の高さがこの程度ならミニスカートの下の下着を見ることができる、というものを示してみる。
 |
32cmの丈の場合、10m(1000cm)離れても、目の高さが150以下の人しか「下着防御ライン」を突破できない。すなわち、女性は事実上「下着を見られる恐れがない」といって良いだろう。もちろん、20mとか離れたら別である。しかし、超人的な視力がなければ、そのような条件下で下着を確認することはできないであろう。
それに対して、30cmの丈の場合には6m離れた時点ですでに視点が2mの位置にある人でも「下着防御ライン」を突破できてしまう。これでは、「全ての人に下着を見られてしまう」ということになる。
もし、女性の身長が20cm程度高く、180cm程度であったら、どうなるだろうか。おそらく、股下長さは10cm程度長くなる。すると、上の図(階段と「下着防御ライン」の差)の緑、赤ラインは10cm程度高くなる。それでも、緑の32cmスカートの「下着防御ライン」はやはり安全圏といえるだろう。
また同様に、厚底サンダル・ブーツなどを履いた場合には股下長さが20cm弱高くなると考えられる。この影響を考えると、長さとしては身長の影響よりも大きいわけである。それは、身長の1/2が股下長さの増加に繋がるのに対し、厚底靴の長さはそのものずばり股下長さの増加に繋がるからである。しかし、それでもやはり緑の32cmの「下着防御ライン」は安全圏である。
すなわち、32cmと30cmのスカートの丈の長さの間には、「下着が見える・見えない」に関する分水嶺が確かに存在するのだ。先の、
「30cmだと下着が見えちゃうしぃ。」という発言は理論的に裏付けられたのである。
それでは、次に階段の角度が25度である場合の計算をしてみる。
 |
緑の線、すなわちスカートの丈が32cmの場合の「下着防御ライン」が階段にどんどんすり寄っているのがわかると思う。すなわち、「下着防御ライン」はより強固なモノとなっているのである。階段と「下着防御ライン」が女性から離れるほど近づくのである。次に、階段と「下着防御ライン」の差を見てみよう。
 |
緑線、すなわちスカートの丈が32cmの場合に注目する。 女性から、離れても、近づいても、何人たりとも、下着を見ることはできないのだ。下着がシュバルツシルト半径の中に隠されるといっても良い。女性の安全を確保する「完全安全条件」を満たす「下着防御ライン」が完成されているのだ。
これは階段と「下着防御ライン」が平行である条件を境として、そのような条件が達成される。その条件よりより「下着防御ライン」が強固になると、誰も「下着防御ライン」を突破することはできない。すなわち、「完全安全条件」が達成されるのである。
この絶対に下着を防御可能(「完全安全条件」)な「完全安全条件」とは、階段と「下着防御ライン」が平行である条件であるから、ミニスカートの丈(xcm)をパラメータとして、
Tan[階段の角度] = (x-25)/14で計算することができる。ここで、14は腰回りの半径(cm)であり、Hip88cmの人の場合である。もちろん、極端な安産体型の場合には、その14という値を適当に補正する必要がある。
さて、この条件には女性の身長(股下長さ)は関係しないところが面白い。もちろん、厚底サンダルなどを履いても同じである。もちろん、若干の影響はあるが、あまり影響はない。
さて、今回の「ミニスカートの幾何学」の考察により、判明した結果をまとめてみよう。
ミニスカート内部の下着が「見える・見えない」には
- ミニスカートの丈が30cmと32cmの間に、分水嶺が確かに存在する
- 絶対に下着を防御可能(「完全安全条件」)なミニスカートの丈(x cm)とは、Tan[階段の角度]= (x-25)/14 により決定される
- ここで、14は腰回りの半径(cm)であり、Hip88cmの人の場合である
- 極端な安産体型の場合には、その14という値を適当に補正する必要がある
- 一方、ミニスカートを履いている人の身長はほとんど影響を及ぼさない
- 厚底サンダルの方が身長よりは影響を及ぼすが、それでもほとんど影響はない
ミニスカートを身につける女性の経験に基づく、「30cmだと下着が見えちゃうしぃ。」理論はなかなか正しいことがわかる。経験というものを軽んじてはいけない、という良い?例かもしれない。結果の伴わない理論に価値はない、ということだろうか。
それにしても、厚底ブーツにミニスカートを履いた女性達は、ロールプレイングゲームの主人公達のようだ。色々なアイテムを手に入れ、冒険を続けている主人公達のようである。ほんの少しだけ、うらやましいような気もする。
さて、こういう話題を書くと少し不安がある。もちろん、私もミニスカートを見ると、妙に心が落ち着かないのも確かに事実ではある。しかし、だからといってことさらに興味津々というわけでもない、と思う。多分。ということで、「できるかな?」の女性読者の数が減少しないことを、ただ祈るのみである。
2002-11-17[n年前へ]
■沼津港で見た景色 
昨日、LUMIX FZ-1を買った。どうしてこの機種を選んだかというと、少し気分を変えてみたかったのである。これまで使っていたNikon775(入院中)を選んだ理由が「小さくて広角アダプターがつくこと」ということだった。だから、今回は「小さくて望遠に強いこと」という風に選んでみたのである。とはいえ、もちろん基本的に私は広角の写真が好きなので、LUMIX FZ-1にも広角アダプターを付けることになるだろう。とりあえず、右の写真はLUMIX FZ-1の広角端で撮った写真で、沼津港の市場から水平線を眺めながら撮った。
そして、左の写真は今度はLUMIX FZ-1の望遠端で撮った写真だ。光学12倍ズームというのはなかなか迫力がある。右の広角端の写真と比べて、その違いが判るだろうか(全然違う写真だけれども)。
しかも、寒い中で手が震えがちで、風が吹いてて、しかも曇り気味で夕日が沈む間際という暗い中にも関わらず、光学手振れ補正のおかげでブレにくかったのもなかなかに良い感じだった。
それにしても、何百回と眺めても、やはり海の近くで眺める青い空はとても綺麗だ。右の写真のような、もうすぐ日暮れという時の深い青とゴールドの空も、日が落ちる瞬間の赤い風景も、日が沈んだ後の藍色の空もどれも本当に綺麗だ。気分はもう、老後の散歩をしている夕暮れ、なのである。
右の写真は、沼津港の市場から外の海を眺めてみた。市場の屋根と柱がまるで写真のフィルムのフレームのように景色を切り取っている感じがとても不思議で天然の展覧会が開催されているみたいだ。不思議な景色だ。



