1998-11-29[n年前へ]
■鴨川カップルの謎 
そうだ、京都、行こう
京都の風物詩の一つに「鴨川カップル」がある。京都を流れる鴨川の川縁に、カップルが等間隔に並ぶ現象である。鴨川の三条大橋から四条大橋までがその舞台である。この鴨川カップルについては、いくつかの性質が知られている。
- 基本的にはカップルらは等間隔に座る。
- 暗くなるに従い、カップル間の間隔が狭まる。
- 電灯の近く、すなわち、比較的明るいところではカップル間の間隔は広がる。
- 夏はカップルの間隔が狭まり、冬はカップルの間隔が広がる。
- 夏はカップル数が多く、冬は少ない。
- 男性が連れ立って、しかも何人かで座っていると、その周りにはカップルはなかなか座らない。
 (四条大橋の上から撮影) |
 |
 |
(この後、1999.05.04午前中に撮影した画像も示す。午前でもあるにも関わらず、上の時より密度が高い。もちろん、夜の密度の高さはこんなものではない)
 |
今回の目的は、「鴨川カップル」のこのような性質はなぜ生じ、そこに効いているパラメータを実測することである。
まず、性質2,3(暗くなるに従い、カップル間の間隔が狭まる、電灯の近く、すなわち、比較的明るいところではカップル間の間隔は広がる)より、明るいと隣のカップルと離れようとする力が大きくなると予想される。また、カップル同士が離れようとする力、斥力、のバランスにより性質1(基本的にカップルらは等間隔に座る)が形成されていると考えられる。
性質3(夏はカップルの間隔が狭まり、冬はカップルの間隔が広がる。)の季節による間隔の違いは性質4のカップル数の違いから来ているのかもしれないし、それ以外の何らかのパラメータがあるのかもしれない。性質4(夏はカップル数が多く、冬は少ない)はやはり「寒さ」のせいであろう。京都は本当に寒い。いくらアツアツのカップルとは言えども、寒いものは寒い(多分、想像だが)。当然、建物の中でのデートとなるだろう。自ずと、鴨川カップルは少なくなる。
性質5(男性が連れ立って、しかも何人かで座っていると、その周りにはカップルはなかなか座らない)については、「男性の群れ」というのは普通のカップルに比べて非常に強い斥力が働いていると考えられる。この性質5に関しては、私の実体験を持って語ることができる。私と友人連中が鴨川の川岸に近づくと、座っている鴨川カップルが離れていく、という経験を何度もしたことがある。やはり、強い斥力が働くのだ。
計算は全てMathematica3.0を使った。計算の例をMathematicaのNotebookで示す。また、計算の考え方を以下に示す。
 | 鴨川の川縁を真上から見た所。画面上部が鴨川。画面下部が歩道。画面中央に街灯がある。そのため、画面中央が一番明るい。 |
 | カップル達はこの辺りに座る。 |
 | 対称性を考えて、画面の左半分のみを考える。また、赤い線上にカップルが座るものとする。 |
 | その線上の明るさを模したもの。X=100の所が街灯の直下とする。 このような明かりに照らされた状態で、カップルが照らされているとする。 |
 | 100m内にカップルが5組として方程式を解くとこうなる。棒グラフの先端の位置がカップルの座っている位置を示している。1組目は0m地点、5組目は100m地点、すなわち、街灯の直下である。 明るい所ではカップルの間隔が離れているのが判ると思う。 カップルの居心地(隣のカップルの存在感=隣のカップルの明るさ/距離)はいずれも、8という値である。カップルの居心地指数は少ないほど快適であることを示す。 |
それでは、条件を振ってやってみたい。上からだんだん暗くなっていく。鴨川の半日である。また、カップル数はいずれも100m辺り5カップルである。
 |  |  | 20 |
 |  |  | 16 |
 |  |  | 10 |
 |  |  | 8 |
 |  |  | 6.4 |
昼間はカップルが等間隔であり、夕方になり、街灯で照度分布ができると、カップルの間隔も分布ができている。といっても、そういう条件で解いているのだから、当たり前だが。
また、カップルの居心地は暗くなった夜の方が快適であるのがわかると思う。それは、カップルの様子を見ていても、その通りであると思う。しかし、快適であるからといって、カップルが何をやってもいいという意味ではない。そこは、はっきりしておきたい。
今回は、カップル数を全て同じにしたが、逆に同じ居心地指数であるという条件下で解けば、夜の方がカップルが多いという性質も再現できる。これらの計算モデルと実験を比較していくことにより、鴨川カップルの性質を実証していくことができるだろう。なお、今回は計算の簡単のため、男性連れの効果は組み入れていない。また、いつかもう少しまともな計算をしてみたい。
計算を行った感想だが、実に不毛な計算であった。気が向けば、モンテカルロシミュレーションによる鴨川カップルの検証も行いたい、と思う。が、気が向く日はきっと来ない。
1999-09-17[n年前へ]
■モアレ、デバイス、2項分布の三題話 
淡色インクの副作用
今回は、9ヶ月間も寝かせた伏線にまつわる話である。いや、別に寝かせるつもりは無かったのだが、いつのまにかそんなに時間が経ってしまった。
以前、
という話があったが、その2つを結びつけるミッシングリンクについて考えてみたいと思う。「2項分布のムラについて考える(1999.01.08)」の最後に「今回の話はあることの前準備なので、これだけでは話しが全く見えないかもしれない。というわけで、続く...」と書いた。「その続き」というわけである。始めに「2項分布のムラについて考える(1999.01.08)」の要点をまとめると以下のようになる。それは、
- ランダムと呼ばれるものの内で代表的な2項分布においては、当然のごとく「ある領域での平均値はばらつく」。
- そして、そのばらつきは直感的に考える程度よりももっとばらつく。
- 例えば、2値画像で考えるならば、2048dpi程度の解像度でランダムなデータを並べた場合には、人間の目はざらつきを感じてしまう。
そして、「モアレはデバイスに依存するか?(1998.11.20)」での要点は
- モアレにはデバイス依存性がある
- 線形な重ね合わせが成り立たない場合にはモアレが発生する。
最近のインクジェットプリンターはCMYKの4色インクだけでなく、淡色インクも使うものもある。淡色のインクを使うことで階調豊かな画像を印字できるわけだ。4色インクだけではディザなどを使って、解像度を下げて階調を出さなければならないわけであるが、それが不要になるわけだ。
解像度を下げないですむわけであるから、ディザのざらつきを感じないですむわけだ。しかし、淡色のインクを使った場合の効果というのはそれだけではないように思われる。HP(ヒューレッドパッカード)などのWEBのプリンター紹介を読んでいると、「淡色のインクを重ねて濃度を出す」というような記述を目にする。これは「少なくとも淡色インクでは線形性(あるいはそれに近い関係)が成り立つ」ということだ。
インクジェットプリンターの解像度を上げたときに、インク滴が意図しないところへずれてしまうことはきっとあるだろう。その際に他のインク滴と重なったらどうなるだろうか?意図しなくても他のインク滴との重ね合わせは発生してしまうだろう。
重ね合わせが成り立たない、非線型なインクではモアレが発生する。言いかえれば、意図しない濃度のばらつき・ざらつきが発生してしまう。「2項分布のムラについて考える(1999.01.08)」で考えたようにランダムに重ね合わさるから広い領域では一定だろうというのは予想外に成り立たないのである。でたらめというのは私の予想外に大きく効いてくるのである。
しかし、重ね合わせに線形性が成り立つ淡色のインクではモアレが発生しない。すなわち、いくらランダムにインク滴の重ね合わせが生じてしまったとしても、意図した通りの濃度をだすことができ、ばらつき・ざらつきは発生しないことになる。参考までにインクジェットの印字画像の拡大写真を示してみる。
 |  |
「重ね合わせに線形性が成り立つ淡色のインクではモアレが発生しない。すなわち、いくらランダムにインク滴の重ね合わせが生じてしまったとしても、意図した通りの濃度をだすことができ、ばらつき・ざらつきは発生しない」と、書いただけでは意図するところが伝わらないと思うので、「モアレはデバイスに依存するか?(1998.11.20)」で使った画像を用いて考えてみる。この画像は重ね合わせがある幾何学模様で生じているが、この現象がランダムに起こっているものとして読み替えて欲しい。
 |  |  |
下は、淡色のインクで重ね合わせ(インク滴の意図しない重なり)が生じた場合である。
 |  |  |
なんの模様も生じていなく、意図した通りの画像出力ができているのがわかると思う。
ということで、今回の話(というか前の2回の話)の繋がりは、
淡色のインクを用いたインクジェットプリンターでは、意図しないインク滴の重ね合わせが生じてしまっても、濃度変化が生じにくく、意図しないインク滴の重ね合わせがでたらめに発生してしまったとしても、画像にはあらわれない可能性があるということである。
うーん、マニアックな内容だ。「身近な疑問を調べる」という看板に偽り有り、である。しかも単なる推論だ。
しかし、もしもインクジェットプリンターを買う人がいるならば、淡色のインクを使っているものを購入するといいかもしれない、ということがわかっただけでも良しとしておこう。
1999-09-20[n年前へ]
■深夜特急 '99 
HIRAX発ロンドン行きWEBの旅
新しい情報を探しに
お笑いパソコン日誌 (http://www2s.biglobe.ne.jp/~chic/pilot.html )を見に行くと面白い情報があった。それは、
Webの分離度合いは19クリック分?である。
( http://www.zdnet.co.jp/news/9909/10/www.html)
内容のポイントは
- 「Nature誌の9月9日発行号の掲載された2つの研究が明らかにしているように,WorldWide Webは急速に,1つの有機生命体としての進化を遂げつつある。Webの成長のダイナミクスとトポロジは,物理学の世界のPowerLawとして知られている法則に従っている」
- 「ネットワーク内の2点間の平均最短経路,つまり“直径”を求めることができる。Web上に8億のドキュメントがあるという推定が正しいとすれば,無作為に抽出した2点間の平均“距離”は19リンクになる。」
そうであるならば、ぐずぐずしてはいられない。もちろん、WWW.HIRAX.NETをスタート地点として、WEBの旅を続け、ロンドン中央郵便局を目指すのだ。平均“距離”が19リンクなら案外と近いかもしれない。WEB上で19回位のヒッチハイクをすれば良いことだ。そして、旅の最終地点であるロンドン中央郵便局からメールを出すのだ。「ワレトウチャクセリ」、と。(何のことか判らない人は沢木耕太郎の「深夜特急」を読むべし。)
そう決めた私はビールを片手にユーラシア大陸横断の旅に出かけた。さぁ、右手の親指を突き出し、ヒッチハイクのポーズで(Libretto50だから)、WEBの旅のスタートだ。
0 http://www.hirax.net/もちろん、旅のスタート地点であるwww.hirax.netだ。ここのTopページからの数少ないリンクサイトからLaboFinderへ飛ぶ。1 LaboFinder http://www.labofinder.org/まずは、Linkページへ飛ぶ。2 http://www.labofinder.org/links/links_index.html会員のWEBへのLinkページへ行く。3 http://www.labofinder.org/links/links_member_index.htmlここから、でわとしかずさんの「ある化学者の屋根裏部屋」へ行こう。4 http://www.asahi-net.or.jp/~av4t-dw/index.html次は、化学系サイトへのリンクへ。5 http://www.asahi-net.or.jp/~av4t-dw/link2chem.htmlそして、University of Leeds (United Kingdom)だ。6 http://chem.leeds.ac.uk/default.htmlここのTravel Informationを選ぶ。7 http://www.chem.leeds.ac.uk/Travel.htmlBritish Airwaysへ行く。8 http://www.british-airways.com/もちろん、Traveller's Guide to Londonだ。9 http://www.british-airways.com/london/Resourcesを選んで、10 http://www.british-airways.com/london/resource/resource.shtmlLondon on the Webへ行く。11 http://www.british-airways.com/london/resource/links/links.shtmlThe London Tourist Boardへ行って、12 http://www.londontown.com/Mapsを選ぶ。13 http://www.londontown.com/maps/St.James Parkへ行って、14 http://www.londontown.com/maps/index3.phtml?grid=H7右へ一回移動して、15 http://www.londontown.com/maps/index3.phtml?grid=J7&letter=&street=&titlegif=こんどは上へ移動する。16 http://www.londontown.com/maps/index3.phtml?grid=J6&letter=&street=&titlegif=
さぁ、Trafalger Squareに到着だ。この横にロンドン中央郵便局はあるはずだ。
やっと、Trafalger Squareの近くのロンドン中央郵便局に辿りついた。えっ、単なる画像じゃないかって?まぁいいじゃないの。ここまで、結構時間がかかっているんだから...何しろユーラシア大陸を横断したんだから。それに真っ直ぐ辿りついたわけじゃないし...
それに16回のクリックで辿りついたのだから、最初の19回という予想にも結構近い。
 |
トラファルガー広場をしばらく眺めた後、NotePCを抱えた私は郵便局員に聞いた(心の中で)。
「電子メールを出したいのですが?」すると、彼女(私の想像の中の郵便局員はもちろん女性だったのだ)は
「電子メールを出すのは郵便局からではありません。」と言った(心の中で)。
言われてみれば(心の中で)、電子メールは郵便局で出すのではなかったのだ。別にどこからでも出せるのだった。別にイギリスまで来る必要もなかったのだ。それならば、例えどこであっても私が決めればそこが旅の終点と決めた「ロンドン中央郵便局」だ。旅の終点の「ロンドン中央郵便局」の場所は私が決めれば良いことだったのだ。
何しろ、プロデューサーにゴールを決められているわけじゃないしね。
1999-11-20[n年前へ]
■バナー画像のエントロピー 
がんばれ、JPEG
前回、
で「バナー画像中の文字数とファイルサイズ」に注目し、「文字情報密度」というものについて考えてみた。情報密度を考えるのならば、で考えたエントロピーについても計算してみなければならないだろう。そこで、今回は前回登場したバナー画像達のエントロピーを計算してみることにした。それにより、情報圧縮度について考えてみることにするのだ。
そうそう、今回も「本ページは(変な解説付きの)リンクページであります」ということにしておく。他WEBのバナー画像を沢山貼っているが、それはこのページが「リンクページ」であるからだ。
エントロピーを計算し、画像の圧縮度を調べる際に、今回はファイル先頭の400Byteにのみ注目した。ファイル全体で計算するのは面倒だったからである。各バナー画像でファイルサイズが異なるからだ。そこで、全て先頭400Byteに揃えてみた。
行う作業は以下のようになる。
まずは、画像ファイルの「先頭400Byteの可視化画像」を作成する。これは、各ファイル中の各Byteが8bitグレイ画像であると考えて、可視化したものである。以前書いたように、「てんでばらばらに見えるものは冗長性が低く、逆に同じ色が続くようなものは冗長性が高い」のである。もし、同じ色が続くとしたならば、「また、この色かい。どうせ、次もこの色なんだろ。」となってしまう。次の色の想像がつく、ということはすなわち、情報としては新鮮みのないものとなる。つまり、情報量が少ないのである。その逆に、情報量の多いものは、てんでばらばらで次の色(データ)の予想がつきづらいもの、となるわけである。まずは、そのてんでばらばら具合を「先頭400Byteの可視化画像」で確認する。
次に、てんでばらばら具合をヒストグラムで確認する。各Byteが0から255のどの値をとることが多いかを調べるのである。てんでばらばらであれば、どの値をとる確率もほぼ同じであり、フラットなヒストグラムになるはずである。逆に、ヒストグラム上である値に偏っていれば、値の予想がつきやすく、情報量が少ないということになるわけだ。
最後に、各Byteのデータを「8元無記憶情報源モデル」に基づいて計算したエントロピーを計算した。各Byteのエントロピー、すなわち、平均情報量は最大で8となる。当たり前である。1Byteは8bitであるから、最大限有効に使いきれば、情報量は8bitになる。
それでは、青い「hirax.net できるかな?」バナーを例にして見てみる。
| 文字情報密度 | ファイルサイズ(Bytes) | 画像 | 先頭800Byteの可視化画像 | ヒストグラム | エントロピー(bits/Byte) |
| 35 | 662 |  |  | 7.1 |
この画像ファイルはトータルで662Bytesであるが、その先頭400Bytesの可視化画像はけっこうばらばらである。それは、ヒストグラムをみても確認できる。少し、0近傍が突出しているが、それを除けば、かなり均等である。そして、エントロピー、すなわち、1Byte当たりの情報量は7.1bitである。満点で8bitであるから、7.1bitはなかなかのモノだろう。
それでは、前回登場したバナー画像達に、同じ作業をかけてみる。
| 文字情報密度 | ファイルサイズ(Bytes) | 画像 | 先頭400Byteの可視化画像 | ヒストグラム | エントロピー(bits/Byte) |
| 31 | 874 |  |  | 6.7 | |
| 34 | 648 |  |  | 7.2 | |
| 35 | 662 |  |  | 7.1 | |
| 40 | 763 |  |  | 7.1 | |
| 44 | 1003 |  |  | 7.1 | |
| 54 | 750 |  | 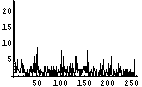 | 7.1 | |
| 58 | 864 |  |  | 6.6 | |
| 112 | 2472 |  |  | 3.8 | |
| 124 | 2348 |  |  | 7.0 | |
| 155 | 465 |  |  | 7.3 | |
| 223 | 3116 |  | 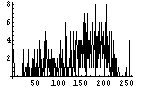 | 7.0 | |
| 294 | 881 |  |  | 6.6 |
IntenetExplorer、RealPlayerといった、ヒストグラム上で突出している値がある画像はエントロピーが少ない。すなわち、平均情報量が少ない。大体、6bit台である。gooは0近傍の値が突出しているのが足を引っ張り、6.6bitとなっている。これらは、1Byteの8bit中の1bit強が無駄となっているわけである。
最高点はMacの7.3bitである。8bit中で7.3bitの情報量を持っているのである。逆に言えば、0.7bitは無駄ということになる。しかし、8bit中7.3bit使い切っているのはなかなかのものである。
それ以外は大体7bit台で拮抗している。しかし、それはいずれもGIF画像である。そう、唯一のJPEG画像である「今日の必ずトクする一言」が3.8bitと低い情報量であるのだ。しかし、これには、いろいろな理由があると思われる。例えば、ファイル全体ではなく先頭のみを見ているため、JPEGのヘッダー部分が入ってしまい、冗長性が高くなってしまっている、とかである。全体でなく、部分で評価しているのは非常にマズイだろう。また、GIFが情報圧縮していることもあるだろう。そのため、JPEG陣営にはかなり不利であったと思われる。
そうそう、今回は情報圧縮度にだけ注目したから、JPEGに不利な結果になった。けれど、他のいろいろな理由を挙げれば、GIFは使いたくないという気持ちもあるのだけれどね。けど、便利なんだよね。
1999-12-27[n年前へ]
■恋の力学 三角関係編 
恋の三体問題
今回はもちろん、
の続きである。前回は、恋の力学を二体間の単純問題に適用したが、今回は複雑系の入門編である三体問題に適用してみたい。二体間の単純問題から三体問題になることで、現実問題に近くなる。また、物語性も大幅にアップする(当社比)。その物語性のいい例があるので、簡単に紹介しておく。小山慶太の「漱石とあたたかな科学」講談社学術文庫の第七章に面白い話がある。- 「明暗」とポアンカレの「偶然」 - である。漱石が、明暗の中でのモチーフにしている「ポアンカレの説明する偶然」について、
- ラプラス -> ポアンカレ -> 漱石
「明暗」の中での登場人物
- 津田
- お延
- 清子
前回の「二体間の単純問題」というのは、「無人島で男と女が二人きり」という舞台設定である。現実にはあり得ない。あぁ、しまった。こう書くと、まるで今回の「三体問題」は「無人島で男二人と女一人」という舞台設定に思えてしまう。これだって現実問題としてあり得ないような気がしてしまう(関係ない話ではあるが、「無人島で男二人と女一人」という舞台設定で始まるジョークは「アメリカ人なら男同士が殺し合い、イギリス人なら紹介されるまで口をきかないから何も起きず、フランス人なら片方は恋人で片方は愛人になり問題は起きず、日本人ならホンシャにどうしたらいいか訊く。」というオチだったように思う。うーん、言い返せない。)。
だが、都会という砂漠が舞台であると思えば、東京砂漠に「男二人と女一人」、あるいは「男一人と女二人」といったような舞台設定は無理がないだろう。そう舞台は東京砂漠ということにしておこう。
それでは、考察を行ってみることにする。まずは解析の条件である。「男」と「女」に関する「恋の力」は前回と同じく、
- 「恋の力」 = 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「同性に対する反発心」 = 「相手の魅力」 * 「二人の間の距離ベクトル」/ 「二人の間の距離スカラー」
- 「恋の力」-「同性に対する反発心」 = 優柔不断度 * 「恋の加速度」
それでは、以下に計算結果をグラフにして示してみる。まずは、「女」「男1」「男2」全員が同じ資質を持つ場合である。この場合、「三すくみ」状態に陥る。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
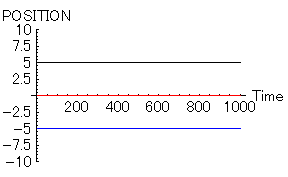 |
この「女」を中心にして、「男」達が身動きが出来なくなった状態はよく見かけると思う。ねるとんなどでよく見かける風景である。ただし、この状態が発生している理由は「男1」と「男2」そして「女」の魅力が全く同じ状態であるからだ。
ほんの少しでも「男1」と「男2」に有利な点があれば、この状態は一変する。次に示すのは「男1」が「男2」よりも1%だけ魅力がある場合である。その1%は理由は何であっても良い。例えば、偶然駅で出会ったなどでも良いだろう。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10.1,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
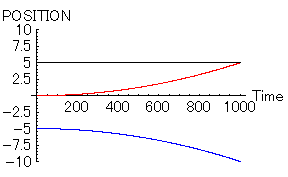 |
その一方、「男1」と「女」は幸せイッパイだろう。クヤシイくらいである。全く...
また、「女」に大きな魅力があった場合には、先の「三すくみ」状態ではなく、見事な「三角関係」に陥る。これは、三すくみ状態を打破するのに十分な魅力が「女」にあるからである。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
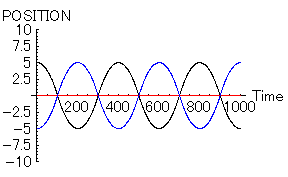 |
「女」を中心にして「男1」と「男2」が右往左往する様子が手に取るように分かる。これも世の中にはよくあるケースだろう。涙無しには見ることのできないグラフである。いや、もしかしたら、私の周りだけかもしれないが...
もちろん、この場合も「男1」と「男2」の魅力にほんの少しでも違いがあれば、状態は一変する。今度は「男2」に「男1」よりも1%魅力が多くあるものとしてみよう。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10.1,優柔不断度=10
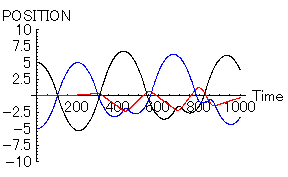 |
「女」の心が「男1」と「男2」の間で揺れ動いている様子がわかると思う。「男」は「恋の力」と「同性に対する反発心の力」により、右往左往状態である。これぞ、リアルな三角関係である。この場合、果たして「男1」が勝つのか「男2」が勝つのか、よくわからない。どの時点で「勝ち」を決めるかで大違いである。また、「女」にすらその結末は予想できないのではないだろうか。「女」自身も相手を決めた本当の理由はわからないと思われる。
これは、もう複雑の極致であるが故に、何の予想もできないのである。
ここまでの話はまるで天文学者が頭を悩ます三体問題のようである(いや、もちろんあちらが本家だが)。天文学者は天体の三体問題に頭を悩まし、我々は恋の三体問題に頭を悩ますのだ。どちらも、実にロマンチックである。
こうして、今回の話の結末はよくわからないままになってしまった。やはり、ここは「明暗」の津田のつぶやき、
「偶然? ポアンカレのいわゆる複雑の極致?なんだかわからない」という言葉で締めくくろうと思う。漱石は偉大である。
さて、「恋の力学」シリーズはまだまだ続く。近日公開とはならないかもしれないが、次回作の予告をしておこう。
- 恋の力学 運命の人編 - 偶然と必然の境界線 - (仮称)