1999-02-28[n年前へ]
■分数階微分の謎 
線形代数、分数階微分、シュレディンガー方程式の三題話
分数階微分?
InterLabの1999No.5を読んでいると面白い記事があった。いわき明星大学理工学部の榊原教授の「Waveletと数式処理ツール」という記事である。といっても、興味を持ったのはWaveletのことではない。もちろん、Waveletに興味がないわけではない。この榊原教授が講師を務めたWavelet講習にも参加したこともある。しかし、今回興味を惹かれたのはその記事中にあった「分数階微分の解析」である。InterLabの榊原教授の記事を引用すると、-通常微分・積分は整数回実行できるが、分数階微分はこれを分数に一般化したものである。さまざまな物理や工学の現象の記述に使われるようになった-とある。一階微分とか二階微分というものはよく使うが、0.5階微分などというものは使ったことがない。どのようなモノなのかさえよくわからない。
参考:
一体、どんな物理や工学の現象の記述に使われているのか知りたくなったので、infoseekで調べてみる。すると、いわき明星大学の清水・榊原研究室の「粘弾性動モデル」が引っ掛かる。
参考:
衝撃吸収・シリコーンの弾性率などに興味を持っている人には面白いかもしれない。もう少し調べてみると「バナッハ空間バナッハスケールにおける分数階積分作用素」というようなキーワードも引っ掛かる。
そこで、まずは勝手に分数階微分について考えてみた。
分数階微分・積分の勝手な想像図
まずは、イメージを考えるためにグラフを作成してみる。x^2の関数、および、それを微分・積分した関数である。微分は3階まで、積分は2階まで行っている。
 |
このグラフ形式の表示をちょっとだけ変えてみる。
 |
ここまでくると、平面グラフにしてみたくなる。つまり、微分・積分の階数を離散的な整数値でなく、連続的な値としてのイメージに変えたくなる。
 |
これで、微分・積分が整数階でない場合のイメージ(勝手な)ができた。微分・積分が離散的なものではなくスムーズにつながっているものであるというイメージである。図.2から図.3への変化をよく覚えていてほしい。
といっても、これは数学的なイメージのみで物理的なイメージはまだここでは持っていない。位置、速度、加速度などの微分・積分で選られるものに対して同じようなイメージを適用すると、位置なんだけれどちょっと加速度っぽいもの、とか、速度と加速度の「合いの子」みたいなものというような感じだろうか?
さらに、これから先は、f(x)という関数が示す無限個の値を位置ベクトルと考えて、f(x)というのは無限次元空間の一つの点だというイメージを持つことにする。線形代数を考えるならそれが一番わかりやすいだろう。任意の階で微分された関数群が集まって、さらに高次元の空間をなしているというイメージである。
分数階微分を調べる
勝手なイメージはここまでにして、手元にある数学の参考書の中から手がかりを探してみた。すると、大学院入試問題解説 - 理学・工学への数学の応用 - 梶原壌二 現代数学社ISBN4-7687-0190-6
の中に手がかりがあった。あれ、ということは以前にやったはずなのか...そう言えばおぼろげな記憶がちょっと...
その中の言葉を少し引くと、
フーリエ変換は等距離作用素である、関数空間L^2(R)における回転といえる。結局、
となる。そして、古典力学におけるハミルトン関数において、運動量を微分演算子で置き換えれば、量子力学や量子化学のハミルトン演算子が得られ、シュレディンガー方程式などにつながるのである、とある。他の資料を眺めてみると、どうやら量子力学などの分野からの要請に応じてここらへんの微分演算子の分野が発展しているようだ。理論物理などをやった方ならよくご存知のことだろう。例えば、水素原子の基底状態の波動関数へ運動エネルギーの演算子を作用させるというような、基本的な所でも、このフーリエ変換を用いた微分演算が用いられてる。ここで、fは元の関数であり、Fはフーリエ変換
さて、この式自体は非常に簡単である。それにイメージも湧きやすい。
i を掛ける演算、私のイメージでは複素数空間の中で90度回転をする(言い換えれば、位相が90度ずれる)演算、が微分・積分であるというイメージはスムーズに受け入れやすい(それが正しいかどうかは知らないが)。なぜなら、微分が空間の中での回転であるとすると、三角関数の微分・積分に関する性質(例えば、Sinを微分するとCosに、Sinを2階微分すると-Sinになる、すなわち、一回の微分につき位相が90°ずつ回転する(位相がずれる)というような性質)が納得でき、それがフーリエ変換という形で登場してくることがスムーズに受け入れられるのである。また、微分といえばとりあえず三角関数の登場というイメージもある。
もう少しわかりやすく書くと、
- 三角関数では一階微分の結果は90度位相がずれる(回転する)。
- ならば、(例えば)0.5階微分は45度位相をずらせば良い。
- 任意の関数もフーリエ変換により、三角関数に分解される。
- ならば、任意の関数に任意の実数値の微分が成立する。
任意の関数をフーリエ変換し三角関数に分解した時の位相、言い換えれば、周波数領域での位相ずらし、で分数階微分が定義されるということは、物理的実用的に大きな意味を持つ。例えば、電磁波、弾塑性運動などの物理現象の中での位相変化を分数階微分で解けることになる。例えば、複素貯蔵弾性率などについて分数階微分との関係は深そうである。あるいは、媒体中の電磁波の位相などについて適用するのも面白そうである。
分数階微分を使ってみる
よく分からないところも多いが、とりあえず、
という式を使ってみる。まずは、使ってみないとわからない。とりあえず、1次元の関数を作成して、この式を適用してみる。まずは、よく出てくるガウス分布で適用してみる。まずはガウス分布とそれの通常の一階微分の解析解を求める。
 |  |
それでは、今回の方法による一階微分の結果と、それと解析解との比較を示す。なお、本来無限領域のフーリエ変換を有限の領域で行っているため、端部近くで変なことが生じるのはしかたがないだろう。また、色々な事情により係数の違いは無視して欲しい。
 |  |
ちょっとずれが生じているが、こんなものだろう。しかし、これだけでは今回のフーリエ変換を用いた微分の面白さはでてこないので、0から2の範囲で連続的に分数階微分をしてみる。
 1/10 (=0.1)階微分 |  1/2 (=0.5)階微分 |  7/10 (=0.7)階微分 |  1階微分 |
 13/10 (=1.3)階微分 |  15/10 (=1.5)階微分 |  17/10 (=1.7)階微分 |  2階微分 |
モーフィングのようで面白い。
さて、今回は分数階微分を勉強してみる所までで、これの応用は別に行ってみたい。もちろん、言うまでもないと思うが、間違いは多々あると思う。いや、田舎に住んでいるもので資料がないんですよ。
1999-03-05[n年前へ]
■できるかな 
ドアの向こうには、
本サイトとドラえもんの共通点
以前、「iMacはドラえもんの夢を見るか?-さようなら、ドラえもん -(1999.02.03)」 の時にドラえもんの話を出した。今回もまたまたドラえもんの登場である。私はドラえもんをさほど読んでいたわけではない。しかし、ここまでドラえもんにこだわるのは、高校時代のサミー本田先生の教育の賜物なのかもしれない。今日(1999.03.05)の朝日新聞の朝刊に4面全面を使ってドラえもんの映画の広告が載せられていた。その内の1面を少し加工したものが下の写真である。
 |
「できるかな」がメインテーマの本サイトとしては、この「できたらいいな」というのは非常に興味を惹かれるコピーである。また、下に示す面の広告のコピーは「iMacはドラえもんの夢を見るか?-さようなら、ドラえもん -(1999.02.03)」 の時に最後に浮かんでしまった疑問の一つの答えであるようにも思う。
 |
「できたらいいな」という気持ちは、その答え故に起きるのであるし、だからこそ「できるかな」という考えが湧くのである。
ところで、本サイトの「できるかな」の名前の由来は「ノッポさんとゴン太くん」の「できるかな」、そして、西原理恵子の「できるかな」である。
- NHKの「できるかな」ビデオ情報 (http://www.nhk-sw.co.jp/kids/video/01838A1.html)
- 西原理恵子「できるかな」(http://www.fujisankei-g.co.jp/fusosha/senden/980124.html)
- 西原理恵子 「鳥頭の城」(公式サイト)(http://www.jah.ne.jp/%7Eaiai/riezo/index.htm)
おまけ
こういう広告を眺めていると、- ドラえもん
- パンドラの箱
- 量子力学
「クジラは哺乳類か魚類か?、論ぜよ。」
という題目であった。この題目についてレポート用紙5枚位で説明できるとお考えの方は不可確実である。言い換えれば、自分なりの「動物分類学を構築せよ」と言っているのである。その人の姿勢まで問われる深い問題である。
1999-08-25[n年前へ]
■インラインスケートの力学 (初心者編) 
つま先立ちの180°ターン
今回は滑る道具の話である。シャレではないが、私はスキーが好きだ。そして、最近インラインスケートを始めた。使っている道具はこんなものである。
- Dynastar AssaultSuperior
- Hart FreeLaunch
- K2 BING AIR
| Dynastar AssaultSuperior (右) Hart FreeLaunch (左) | K2 BING AIR |
 |  |
それぞれの滑走接地部の長さはDynastar AssaultSuperiorが185cm程であり、Hart FreeLaunchが110cmである。K2BING AIRは26cm位だ。
Dynastar AssaultSuperiorの長さを1とすれば、Hart FreeLaunchは長さが0.6程度である。半分とは言わないが、かなり短い。75cmも違う。しかし、この程度の長さにしたくらいではそれほど不安定になるわけではない。特にHart FreeLaunchは安定性が抜群である。私もゲレンデで普通に滑っている限りでは、遅い方ではないと思うが、特に不安定になることはない。不安定だと感じるのは、コブ斜面で、なおかつ、雪が積もってコブの形状が見えない場所を滑る場合などである。それほど、安定感があるのである。
そして、スキー板が短いため、ターンのしやすさといったら素晴らしいものだ。1つのコブの上で、2回3回とターンが出来る。
さて、今回の本題のインラインスケートはと言うと、かなり接地長さが短いため、さすがにスキーに比べて不安定さを感じる。とはいえ、思ったよりも不安定ではなかった。(初心者の頃の)スキーで曲がる時のことまで考えたら、もしかしたら、スキーよりも転びにくいかもしれない。急角度のターンのしやすさといったら、Hart FreeLaunchの比ですらなく、瞬時の180°ターンなども簡単である(私は上手くないが)。
今回はインラインスケートにおける瞬時の180°ターンの力学について考察を行ってみたい。瞬時の180°ターンに必要なことは以下のようなものである。まず、前向きに進んでいる状態から瞬時に後ろ向きになって進む場合を考えてみる。状態の変化は以下のようなものだろう。
- 前向きに進んでいる。
- スケートを瞬時に回転させる。
- スケートが180°回転した、すなわち、反転したところでスケートの回転を停止させる。
- そのまま、後ろ向きになった状態で進行する。
- 前向きに進んでいる。
- スケートブーツの爪先で立つ。
- スケートブーツが勝手に180°回転し、反転したところでスケートブーツの回転が勝手に止まる。
- いつのまにか、後ろ向きになった状態で進行している。
まずは、足を回転させてみると、その回転軸は下の図で紫の円で示したような場所に位置することがわかる。土踏まずと中指の根元の中央辺りである。
 誰がなんと言おうとこれは「足」 |
この図を「インラインスケートのブーツを履いた場合」で示したものを以下に示す。
 |  |
それでは、つま先で立ってみよう。どういうものに近似できるだろうか?
 |  |
何か見覚えがないだろうか? そう、台車の足部分である。ここまでくると判りやすい。台車の場合で考えれば、良く実感できる筈である。
 |  |
それでは、簡単な力学計算をしてみる。「足の回転軸」と「地面に接触しているローラ部分」を拘束系の剛体問題と考えてみよう。インラインスケートのローラは「足の回転軸」と「地面に接触しているローラ部分」を結ぶ方向にはいくらでも回転できる。したがって、転がり摩擦を無視すれば、その方向に関しては「地面に接触しているローラ部分」は地面からは何の力も受けない。しかし、ローラは「足の回転軸」と「地面に接触しているローラ部分」を結ぶ方向と直行する方向には回転することができない。したがって、その方向へ地面から力を受けることになる。滑っている人の速度をVとすれば、「地面に接触しているローラ部分」が「足の回転軸」と「地面に接触しているローラ部分」を結ぶ方向と直行する方向に受ける力はVsinθである(シータは文字化けしそう...)。
 |
もうここまでくれば、一目瞭然である。「インラインスケートを回転させる力」であるVsinθ(シータは文字化けしそう...)をグラフにすると以下のようになる。ここで、θ(シータは文字化けしそう...)がPiを過ぎたところで、-Vsinθ(シータは文字化けしそう...)になっていることに注意してもらいたい。
 |
このグラフは縦軸が任意単位の「インラインスケートを回転させる力」を示しており、横軸がインラインスケートの回転軸に対する角度である。ちょっとでも、インラインスケートが回転軸に対して傾くと(θ(シータは文字化けしそう...)=0でなくなると)つま先を後ろへ向かせる方向へ力が働き急激に回転する。そして、つま先が真後ろを向き始めるとその力は弱くなる。つま先が真後ろを向いたところで、その力は0になり、もし回転しすぎると、また、真後ろへ戻す力が働く。そなわち、つま先が真後ろへ向いているのが非常に安定なわけである。
というわけで、インラインスケートで前進中に爪先立ちすると、何も考えなくてもちょうど180°回転してくれるというわけである。もちろん、後ろへ進んでいるときに回転したいならば、進行方向側のかかとで立てば良いわけである。
今回の話はひとまずこんなところである。
1999-10-31[n年前へ]
■ビックエッグの力学 
ドームを支える空気圧の謎
この回は(トンデモ話)であり、中途半端であるのだが、反省を込めてこのままにしておく。直すのが、面倒くさいわけではないので、念の為。
日本シリーズ'99をやっている(いた)。私は野球は特に好きでも嫌いでもないが、野球場でビールを飲むのは大好きだ。そういえば、今年はドーム決戦である(だった)。ドームといえば元祖「東京ドーム」だろう。「東京ドーム」のWEB
- 株式会社東京ドーム (http://www.tokyo-dome.co.jp/about/index.htm )
| 東京ドームは、空気膜構造によるエアドーム。つまり内部気圧を外気より0.3%高くして、400トンもの超特大楕円形の屋根を膨らませるのがドーム建築のポイントなんだ。 ところで、この気圧差0.3%は、ビルの1Fと9Fぐらいの違いがある。とはいえ中と外の違いを体感することはほとんどない。 |
たった、0.3%の空気圧の差で400トンを支えるとは、ものスゴイ。すぐには納得できない数字である。別に疑い深い私でなくても不思議に思うことだろう。
そこで、確かめてみることにした。まずは、東京ドームの面積をx(m) * x(m)としてみる。すると、持ち上げることのできる重さ(トン)は、
- 0.3 / 100(%から比へ) * 100(hPaからN/m^2へ) * x * x / 1000(kgからトンへ)* 9.8(Nから重力へ)
と計算できる(この式には実は間違いがある。詳細は後で...)。その結果を示してみる。
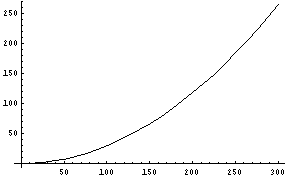 |
先の、Webから東京ドームのサイズを見てみると、x = 180mである。すると、持ち上げられる天井の重さは100トン程度であるということになる。おやおや、先の「400トンの天井を持ち上げる」というのとはずいぶん違う。これでは、天井を支えきれない。
 |
そこで、高さによる大気圧の差を導入し、天井近くの高い場所では「外部の気圧が低い」という条件を導入してみる。0.3%というのは地上での比で、天井のある上空ではさらに差があるとしてみるのだ。うーん、強引である。
さて、ここから後は(実は前も)トンデモ話になっているので眉に唾をつけて読んで欲しい。それを指摘して下さった、読者からの手紙への返事(とほぼ同じ内容)を下に示しておく。
青木さんへの手紙> 高さによる圧力の差は、高さの異なる二点間に存在する空気> の重さに見合ったものです。したがって、ドームの内部でも> 高いところほど圧力は低くなっている筈です。 その通りだと思います。WEB中で「うーん、強引である。」と書いたのはまさにその理由です。 それにも関わらず、強引な論法を続けたのは、文章の最後に「謎は解けないのに、東京ドームは存在している。 少し、くやしい。 」と書いた理由と同じです。まるで、「宇宙人が水道橋の駅前駐車場にUFOを停めて、サラ金に入って行くのを目の当たりにしている」ような、気持ちなのです。くやしいと強引になるのです。あぁ、何て人間らしいのでしょうか... また、計算をしていた時に少し勘違いをしていました>もし、ドームの内外の温度が等しければ、地上でも天井でも内外の差圧は>同じになるはずです。と仰るとおり、差圧は等しいわけですが、それを0mにおける大気圧に対するパーセンテージに直すと、高度が高くなればなるほど、そこの気圧に対してはパーセンテージは高くなります。計算をしていた時にその「パーセンテージが高くなる」ことを「差圧が高くなる」ことと同じに扱うという間違いを犯してしまいました。もちろん、基準の気圧が小さくなっているので、パーセンテージが高くなっても本当は差圧は変わらないわけです。「考えることを手抜きしていた」と言ってもよいかもしれません。要反省です。>ドーム内の温度が高ければ空気の密度> が減少し、天井の位置での差圧はより大きくなり、天井を支> えるのに有利に働きます。これは、浮力によって天井が持ち> 上げられていると考えても同じ事です。> という訳で、ドーム内外の温度差が逆転する夏と冬とでは天> 井を支えるのに必要な圧力を変えなければならないと思うの> ですが本当はどうなんでしょうか。 これは面白そうですね。そういえば、学生時代に地殻物理学を専攻していたのですが、夏と冬の大気圧の違いから、地殻歪の大きさに関係づけて、地震の予言をするなら、「冬に発生する」といった方が良い、話(もちろんかなり冗談で)をしていた先生がいました。その先生に「今回のトンデモ話」がばれたら、大目玉をくらうこと間違いなしです。 ビックエッグの謎は深まるばかりです。それでは、また。------------------------------------------------------------------ch3coohさんへの手紙> > >12/(100*100)*1000= 1.2g/cm2となります。> > >> > >地上での大気圧は約1Kg/cm2なので、上の値は> > >1.2%程度となり、 ここが疑問だったのですが、これは1.2%でなくて、0.12%ですね。なるほど、0.3%よりも小さいですね。実に納得です。 さて、他の方からの指摘もあり、私の計算には> >0.3 / 100(%から比へ) * 100(hPaからN/m^2へ) * x * x > / 1000(kgからトンへ) * 9.8(Nから重力へ)> に1013(標準気圧 hPa)がかかっていないことが気になりました。 という間違いがあることがわかりました。全てはここが原因だったようです。 全ての疑問が解決しました。いやぁ、お恥ずかしい。また、他にも色々と面白い情報ありがとうございます。
ひとつわかったことは、間違いをすると読者からの手紙が沢山来るといううれしくもつらい事実であった。ここから、あとは封印したい思いで一杯なのだが、自戒を込めてこのままにしておく。しつこいようだが、直すのが面倒なのではない。
それでは、高さによる大気圧の差を計算してみる。理科年表から15℃の「標準大気の場合の高さと気圧の表」を見てみる。 ちなみに、東京ドームの温度は、「ガス熱源による冷暖房システムにより、夏期は28℃の冷房、冬期には18℃程度の暖房が行われている」とある。今回の計算は外気の温度が15℃で、内部は冬期には18℃程度の温度に調整されているものとしておこう。
標準気圧は海抜0mで1013mbであり、200mでは989.5mbである。理科年表が古いのでPascal値でなく、mb表示になっている。
これから、1m当たりのmb変化を計算すると、0.12mb/mとなる。比率に直すと、0.012%/mということになる。例えば、「ビルの1Fと9Fぐらい」の高さの差は30m位であろうから、それを大気圧の比に直すと、99.6%位となり、先の記述と大体合う。
以下に、高度に対する大気圧の差(の比 %)を示してみる。
 |
このグラフで30mの場所を見てみると、99.6%位というわけだ。これが、先のWEB上の「この気圧差0.3%は、ビルの1Fと9Fぐらいの違いがある。」という説明と合うわけである。
次に必要なのはドーム外部と内部の大気圧の比から、力に直してみる。基準面からの高さ0mにおける気圧を1hPaとして、1hPa = 10^2 N/m^2 = 10^2 m^-1 kg s^-2という単位換算を使うと、持ち上げることのできる重さは、
- (100-大気圧の差(の比 % )) / 100(%から単なる比へ) *9.8(重力に換算) / 1000(kgからトンへ)* 100(hPaからN/m^2へ) * x^2(ドームの面積)
東京ドームの高さは「グラウンド面から 61.69m」とあるので大雑把に100mとしてみる。
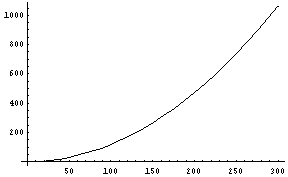 |
この計算結果によれば、東京ドームのサイズを180mとした時には、「持ち上げることのできる力」は400トン位になっている。ということは、先のWEBの記事と大体一致するわけである。
しかし、この計算では致命的な欠陥がある。天井の高度が低いときには、400トンを持ち上げるためにはもっと高い「ドーム内部の圧力を必要とする」ことだ。
例えば、0.3%空気圧の差の条件で、「天井の高度」に対する「持ち上げることのできる力」を計算してみると、次のようになる。
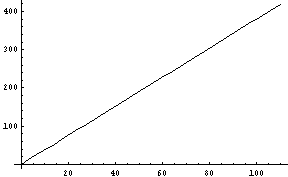 |
これでは、天井の高さが下がるとますます天井の重さを支えきれなくなってしまう。それに、そもそも天井をどうやって持ち上げたのだ?屋根を持ち上げるインフレートという作業はどうやって行ったのだろう?
今回の計算は謎が増えただけかもしれない。謎は解けないのに、東京ドームは存在している。
少し、くやしい。
1999-11-13[n年前へ]
■やっぱり、ウニが好き ! 
Dr.フラーはウニの夢を見るか?
私は野球は特に好きでも嫌いでもないが、野球場でビールを飲むのは大好きだ。と、始めると
の間違いと思われるかもしれない。しかし、それは違う。今回は、ウニとドームハウスの共通点について、考えてみたい。ただ、かなりビールが脳みそにしみているせいか、少しドンデモ話になるかもしれない。そこは、「ビックエッグの力学」と共通である。 私の中では、野球観戦と言えば、ビールだ。野球にはビールが良く似合う。そして、今現在も目の前にはビールがある。そして、寿司がある。といっても、スーパーで買った安物である。二つ合わせても1000円にしかならない。
 |  |
安物といっても、私の住んでいるのが港町だから安い、ということもある。何しろ、ほとんどのスーパーの魚売り場でイルカの肉なども置いてあるのだ。嘘ではない。ホントにホントである。私も、引っ越してきた当時はビックリしたが、本当である。アメリカの動物愛護団体が見たらびっくりの風景だろう。「イルカと人間はお友達」と言ってる人には見せられない風景だ。
あまりおいしそうではないので、私はまだ実際に味わってはいない。しかし、地元の人の中には「よく食べる」と言う人もいる。いつか、挑戦してみたい。
さて、上の写真で共通しているのはウニである。ウニと言えば、こんな姿をしている。
 |
「海栗」と書いてウニと読むことが実に納得できる姿である。しかし、内面はもう少し違う。実は、ウニはドームにそっくりである。前回考えたドーム球場ではないが、ウニは実はドーム構造をしているのだ。「そんなことは当たり前じゃないか」と言う人もいるだろう。しかし、私はつい最近までそれを知らなかった。そもそも、骨があるとすら思っていなかったのである。
もしかしたら、私のようにウニの内面を知らない人もいるかもしれない(そんな人はいない、という声も聞こえそうだが)。そこで、ウニの骨の写真を示してみる。下に示すのが、色々なウニの骨だ。
 実物はとてもきれい。日本古来の木工細工のような穴がとてもきれいである。 |
これは少し前に、宇宙科学研究所の黒谷氏の実験室を見学(ただ邪魔しただけという気もするのであるが)する機会があり、そのとき頂いたものである。最初に見たときは、「目からウロコ」であった。まさか、あの針の山の下にこんな頑丈な殻が存在しているとは、思わなかった。
写真ではわからないかもしれないが、骨には小さな穴が極めて規則的に開いている。それが、日本古来のとても出来がいい木工細工のようである。光に透かしてみると、うっとりするようなきれいさである。内部に強い光源でもおけば、プラネタリウムやミラーボールみたいに細い光線を放射する、きれいなアクセサリーができそうだ。
ところで、「何故、宇宙科学研究所の実験室にウニが?」と思われる方は、WEBで検索でもかけてみると良いかもしれない。「宇宙生物学」という面白い実験分野があるものだ。
例えば、無重力の中で生物がどのような挙動を示すか、などの研究をしたりするらしい。飛行機にのってそういう実験を繰り返すわけである。遊園地のフリーファールやバンジージャンプ、そして、ジェットコースターでさえ、駄目な私には地獄のような研究分野である。
さて、上の、ウニの骨の姿はまさにドームそのもの、とは思えないだろうか? そう、似ているのだ。 そっくりなのだ。試しに、このドームなどを見れば納得できるだろう。
 |
これは、富士山頂の厳しい環境を耐えるために、極めて安定なドーム構造が用いられているのだ。三角形のパネルが組み合わさるドームハウスは極めて頑丈である。ウニも、同じように頑丈なドーム構造の骨格を持っているのである。レーダードームは富士山頂で頑張っているが、宇宙科学研究所のウニは色々なところへ連れて行かれて、厳しい実験に耐えているのである。
こういった、ドームと言えば、R.バックミンスター・フラー博士のドーム理論だろう。フラー博士とドームハウスのスケッチ図を示してみる。
|
よく、環境適応性の高さを謳うことの多いドームハウスであるが、もしかしたら、ウニがその祖先であるかもしれない。もしかしたら、フラー博士は「海の中でじっとたたずむウニの夢を見て」ドームハウスを思いついたのかもしれない。
アメリカ人であるフラー博士がウニを食べたとは思えない、という人も多いだろう。それは確かにその通りである。しかし、フラー博士はかなりの変人である。変人ならば、ウニを食べまくっていたとしても、おかしくはない。
普段は「何を馬鹿な発想だ」と思うことだろう。しかし、ドーム球場の野球を見ながら、脳みそがビールとウニで満たされてしまうと、「そうだ、フラー博士はウニが大好きなのだ!そうに違いない!」と確信してしまうのだ。
仮に、フラー博士がウニに影響されていないとしても、ウニはフラー博士がドーム理論を考えるずっと太古の昔から、ドーム構造をしていたのである。ならば、「元祖はやはりウニなのだ!」と言ってしまって良いだろう。太古から厳しい環境を耐えつづけてきたウニは、今や宇宙へ飛び出し、さらに厳しい環境の中で活躍しているのである。

