hirax.net::Keywords::「揺れ」のブログ

■ブランコの中の∞(無限大)　

なんで一体漕げるのだろう？

　もちろん、そこは子供の領分というだけではなくて、黒沢明の「生きる」の主人公がしていたように「大人がブランコに座って揺れていたり」すると、思わずその人の陰に隠れている物語を想像したりしてしまう。ブランコの周りというのはそんな不思議な雰囲気を持っているのだ。

　やたらにブランコを漕ぐのが上手いガキんちょもいる一方で、全然ブランコを漕げず四苦八苦する子供もいる。ブランコを漕ぐコツを覚えるのもなかなか大変そうである。考えてみれば、ブランコは一体どういう風に漕ぐものなのだろう？口で上手く説明できる人がいるだろうか？

　それに、そもそも私たちはブランコを何故漕ぐことができているのだろう？

　いったい、いつから疑問に思うことをやめてしまったのでしょうか?　いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか?
　いつだって、どこでだって、謎はすぐ近くにあったのです。
　何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。

　もちろん、「何でブランコの漕ぎ方が不思議なのさ？」と言う人も多いだろう。その中には理路整然とブランコの漕ぎ方を説明してくれる人もいるだろう。そして、「特にブランコの漕ぎ方をじっくり考えたことなんかないもんね」という人も多いに違いない(私だけかもしれないが)。そこで、まずは「ブランコの不思議」を簡単に書いてみることにしよう。

　次の図は「ブランコを漕いでる子供」である。
 

ブランコを漕いでる子供

　この子供が何もせず立っているだけ(あるいは座っているだけ)だったら、どうなるだろうか？それはもちろん、単なる振り子と同じくようにブランコは動く。もしも色々な摩擦がなければ、まったく同じように動き続けるだけだし、摩擦力があればブランコの動きはただ減衰していくだけである。つまり、子供が何もしなければ、ブランコの動きは「遅く・小さく」なることはあっても、ブランコが「速く・大きく」なることはないのである。

　だからブランコを速くするためには、「ブランコに乗ってる子供がブランコを漕がなければならない」わけであるが、ブランコに乗ってる子供は一体どんなことができるだろうか？

　次に示す図は「ブランコに乗ってる子供を中心にとった座標軸」を描いてみたものだ。この図の中で直交する二つの軸を描いてある。つまり、

1. ブランコの動きの中心を向いている軸A
2. 軸Aに直交する、つまりブランコの進行方向(あるいはその逆方向)を向いている軸B

ブランコに乗ってる子供を中心にとった座標軸

　ところが、実は「ブランコに乗ってる子供」はこの二つの軸の内の片方、軸Aに対しての動きしかできない。何故なら、軸B方向に対しては「ブランコに乗ってる子供」動きの支えになるモノが全然無い。だから、ツルツル滑る氷の上では全然動けないのと同じく、「ブランコに乗ってる子供」はその方向には動けないのである。もし子供がその方向に動こうとして体を動かしたりしても、結局子供の重心はその方向には全然動かないのだ。

　それに対して、ブランコの動きの中心を向いている軸A方向に対してはブランコの鎖も座っている(あるいは立っている)板が支えになるわけで、その方向に対しては「ブランコに乗ってる子供」は動くことができる。

　というわけで、ブランコの上では「ブランコの動きの中心を向いている軸A」方向にしか動けないわけであるが、その方向というのはブランコの進行方向に対しては直交している。つまり、ブランコを漕ぐためには、「ブランコの進行方向に対して直交している方向に動く」しかないことになる。

　ここまで書くと、ブランコの不思議が判るハズだ。ブランコを漕ぐ、つまりブランコを軸B方向の速度を上げたいのに、我々は「軸Bに対して直交している方向に動く」ことしかできないのである。一体何故、軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増すのだろうか？　この謎「ブランコの不思議」を、ゆっくり考えてみることにしよう。
 

　まずは、ブランコに乗ってる子供が立ち上がったりして、「ブランコの動きの中心を向いている軸A」方向に動いた場合、何が起きるだろうか？
 

ブランコに乗ってる子供が立ち上がったりすると、何が起きる？

　「ブランコの動きの中心を向いている軸A」方向に動くと、ブランコの鎖の長さが短くなることと同じである。すると、回転しているブランコの鎖が短くなるわけで、そうするとブランコの速度は速くなる。何故なら、角運動量が保存されるからである。ちょうど、スケートのフィギア競技の選手が回転中に伸ばしていた手を縮めると回転数が早くなるのと同じだ。

　もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの半分だけ(とんでもない身長の子供だ！)上がれば、ブランコの速度はもとの速度の倍になるのである！

　ということは、少なくともこの瞬間は「軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増す」わけであるが、これでブランコの漕ぎ方を納得するにはまだまだ早いのである。確かに、「ブランコの動きの中心を向いている軸A方向に動く」とブランコの速度は増すわけであるが、それはその瞬間だけである。ブランコの上で「立ち上がり続ける」なんてことはできないわけで、速度が増し続けるわけではないのである。

　もしも、「もう一度ブランコの上で立ち上がるために、すぐに低い姿勢に一旦戻ったり」したら大変だ。ブランコの鎖の長さが長くなるのだから、今度はブランコの速度は遅くなってしまうのである。

　もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの二倍だけ(つまりさっき立ち上がった逆の動きである)下がれば、ブランコの速度はもとの速度の1/2になってしまうのだ！
これでは、結局さっきの速度が二倍になったことは帳消しになってしまう。つまり、「単純に」角運動量の保存を考えるだけではブランコの速度を(長い間にわたって)早くしていくことはできないわけだ。

　このままでは、「ブランコを漕ぐことなんか不可能である」という結論が出てしまいそうになるが、ブランコを漕いでる子供達はイッパイいるわけで、そんな結論を受け入れるわけにはいかない。彼らがみんな超能力でブランコを漕いでいるわけもないのである。まだまだ見落としていることがあるので、ブランコの不思議の謎が解けないだけのハズなのだ。
 

　そこで、ちょっと考えてみると「とんでもなく単純なこと」を見落としていたことに気付いた。それは、「タイミング」である。例えば、ブランコの速度がずっと同じであるすると、

1. 初期のブランコの速度 = 10
2. 重心位置を高くして 10 X 2 = 20　(やったぁ、速度が二倍だぁ！)
3. 重心位置を低くして 10 Ｘ 1/2 = 10　(何てこったい、速度が半分になっちまったか！)

1. 初期のブランコの速度 = 10
2. 重心位置を高くして 0 X 2 = 20　(やったぁ、速度が二倍だぁ！)
3. そのあとブランコの速度 = 0
4. 重心位置を低くして 0 Ｘ 1/2 = 0　(0が0になっても全然変わってないもんね！ヘヘン！)

　人生何事もタイミングが重要である。失恋した男性や女性にタイミングをわきまえた「恋のハイエナ」達が寄ってくるのと同じく、またお金に困っていると何故かサラ金の広告が目の前にチラチラするのと同じく、ブランコを漕ぐにはやはりタイミングが重要なのだ。
 

　なるほど、考えがまとまってきた。このイキオイでそのまま「ブランコの理想の漕ぎ方」まで考えてしまおう。

　まず、「重心位置を高くしてブランコの速度早くする」にはできるだけ速度が速い瞬間に行うのが良いだろう。倍率が確定している賭なのだから、元金はあればあるほどおトクである。１万円×２=二万円では１万円しかもうからないが、一千万円×２=二千万円では一千万ももうかるのだ。ブランコの速度が速い瞬間に立ち上がれば、一番おトクに速度を増すことができるのである。

　もちろん、ブランコの速度が速い瞬間といえば、明らかにブランコが一番下にきた瞬間である。つまり、ブランコが一番下にきた瞬間に立ち上がれば「一番おトクに速度を増すことができる」わけだ。しかも、その瞬間は鉛直に重心を持ち上げることになる。つまり、位置エネルギーを効果的に増加させることができるわけだ。結局、この時に増加させた位置エネルギーは後で、運動エネルギーに変換されるわけで、結局これがブランコの運動の源となるのである。

　そして、「次にもう一度立ち上がるために一旦低い姿勢に戻る瞬間」=「速度が遅くなる瞬間」はブランコが停止しているときであれば何の問題もない。ブランコはもともと止まっているんだから、その速度が何分の一になったって全然気にしないもんね！となるわけだ。そのタイミング= ブランコが止まる瞬間といえば、もちろんブランコが最高地点まで上がった瞬間である。つまり、ブランコが一番上にいった瞬間に低い姿勢に戻れば全く減速無しに次の加速に備えることができるわけである。しかも、その時には実は運動エネルギーを位置エネルギーに変えることで、隠し財産にしているわけで、もう汚い政治家のマネーロンダリングのような見事な方法なわけだ。

　というわけで、

• ブランコが下に来たときに(立ってる場合は)足を伸ばして立ち上がったり、(座ってる場合は)足を曲げたりすることにより高い位置に重心を持ってきて(しかも、重力に逆らって重心を上げるため位置エネルギーが増加する)
• ブランコが上に行ったときにその姿勢を元に戻す

　それでは、確認のためにそのやり方で本当にブランコが漕げるのかどうか、シミュレーション計算を行ってみた。ブランコの動きは振り子運動だが、振れ幅がとても大きいので、cosx≒xというような近似をする単振動としての扱いはできない。そこで、楕円積分の計算を行わなければならない。が、私が自分の力でできるかどうかはともかく、そこはMathematicaに解かせればイッパツである。もう、驚くくらい簡単なのである。自分の力で解いていないところが、実に悲しい現実ではあるが、それが現実なのだからしょうがない。

　というわけで、ブランコの動きのシミュレーションをしてみた結果が次のグラフである。「ブランコに乗ってる子供」の漕ぎ方としては、以下の三つ

1. 何もしない場合
2. ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合
3. ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合

ブランコの動きのシミュレーション結果

1. 何もしない場合 →　ブランコの動きはず〜と変わらない

2. ブランコが下にきたあたりで立ち上がり、 ブランコが上にきたあたりで座り込んだ場合 →　ブランコの動きはどんどん大きくなる 「やったぜ、これが理想の漕ぎ方だぁ。」

3. ブランコが下にきたあたりで座り込み、 ブランコが上にきたあたりで立ち上がった場合 →　ブランコの動きはどんどん小さくなる 「なんてこったい、遅くなっちまったぁ。」

　この結果から、ちゃんと1.の「何もしない場合」は「ブランコの動きはず〜と変わらない」し、理想の漕ぎ方であるハズの2.の「ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合」は「ブランコの動きはどんどん大きくなる」し、最悪の漕ぎ方であるハズの3.の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合」には「ブランコの動きは逆にどんどん小さくなってしまう」ことがわかる。というわけで、今回考えた「ブランコの不思議= 漕ぎ方」はシミュレーション計算結果からも確かめることができたわけだ。

　ところで、こういったタイミングを考えながらパラメーターを変えることで動きを大きくしたりすることは「パラメータ励振」と呼ばれる。ブランコの漕ぎ方はその「パラメータ励振」の応用のひとつである。「何故、リンゴは落ちるのかという謎」には重力という基本的な物理現象が隠されていたが、それと同じく、「ブランコの漕ぎ方の謎」にも「パラメータ励振」という物理現象が隠されているのだ。次回以降も、この「パラメータ励振」を手がかりにいくつかの「身近な謎」に迫ってみたい、と思うのである。
 

　さて、公園でブランコを漕ぎまくる子供をもし見かけたならば、ぜひ横から子供の動きを見てやってもらいたい。きっと、その揺れ動くブランコの中にはこんな∞(無限大)の形が見えるハズだ。天まで上ろうとする「ブランコの秘密」はその「ブランコの中の∞(無限大)」に隠されていたのである。子供も含めて人間の可能性は∞(無限大)だと私は思うが、ブランコの揺れる動きから、そんなことを考えてみるのも少し面白いのではないだろうか？　それとも、ちょっと考え過ぎかな。
 

■続々オッパイ星人の力学　

胸を揺さぶるパラメータ励振 編

　前回、

• ブランコの中の∞(無限大) - なんで一体漕げるのだろう？- (2000.11.26)

　ところで、公園でブランコを揺らす子供達と同じく、純真でピュア〜なのが生まれたばかりの乳児達である。もちろん、そんな乳児達はまだまだ公園でブランコを揺らすなんてことはできなくて、大きく成長するために母親の母乳を飲んで、そしてただひたすら眠る毎日を過ごしているのである。

　そんな乳児の頃の純真でピュア〜な気持ちを、大人になっても持ち続けている人達もいる。そんな純真でピュア〜な大人達は大人になっているにも関わらず、生まれたばかりの乳児と同じくオッパイに惹かれ続けているのである。そして人は彼らをほんの少しばかりの尊敬と沢山の侮蔑を込めて「オッパイ星人」と呼ぶのである。
 

　これまで「できるかな?」では、そんなオッパイ星人達の科学である

• オッパイ星人の力学 - 胸のヤング率編- (2000.06.29)
• 続 オッパイ星人の力学 - 揺れる胸の動き編- (2000.07.02)

　
　まずは、次に示す「純真でピュア〜」な二つの運動を見てもらいたい。一つは、「純真でピュア〜」な
子供達が公園のブランコを揺らしている時の動きであり、もう一つは「純真でピュア〜」な「オッパイ星人」達が眺めているGカップバストを揺らす女性の胸板の動きである。
 

　この二つの図をじっと眺めてみると、何か共通点が見えてはこないだろうか？少なくとも、私(純という名前を持つ位だから純真さでは保証付きである)と同じく「純真でピュア〜」な目で眺めてみれば、共通点が見えてくるハズなのである。

　「何か、単に両方グニョグニョした動きにしか見えないぞ。」という人、つまり「純真でピュア〜」な目を持たない人もきっと多いことだろう。哀しいことに、この世知辛い世の中ではそんな「純真でピュア〜」な目を持ち続けるのはムズかしいことなのである。そこで、そんな不純な人でも判りやすいように、さらに

• 子供がブランコを動かすときの「子供の上下方向および水平方向の動き」
• 女性が歩くときの「女性の胸板の上下・左右方向ぞれぞれの動き」

ブランコを動かすときの「子供の上下方向および水平方向の動き」を簡易的にしたもの

ブランコを漕ぐ子供の 重心の上下方向への運動

ブランコの水平方向の運動

　そして、こちらが女性が歩くときの「女性の胸板の上下・左右方向ぞれぞれの動き」である。
 

女性が歩くときの「胸板の上下・左右方向ぞれぞれの動き」

女性が歩くときの 胸板の上下方向への運動

女性が歩くときの 胸板の左右方向への運動

　こうしてみると、ブランコを揺らす子供の動きと、Gカップバストを揺らす女性の動きが、よく似ていることがわかるだろう。上下方向への運動は全く同じであるし、左右方向への動きはタイミングが違うだけ、つまり位相が違うだけなのである。その位相の違いを実感するためには、

• 時間
• 左右の動き = X
• 上下の動き = Y

それぞれの動きの「時間・左右動・上下動」

ブランコを揺らす子供の動きの場合

Gカップバストを揺らす女性の動き

　方向性が逆であるだけで、全く同じであることがよく判ると思う。方向性の違いを除けば、ブランコを揺らす子供の動きとGカップバストを揺らす女性の動きは全く同じなのであって、私はこれら二つの運動の根本原理は全く同じものなのではないか、と思うのだ。もちろん、その原理を「純真でピュア〜な心」である、と言ってしまえばそれで終わってしまうわけなのだが、それでは「科学(?)」ではない。「純真でピュア〜な心」がブランコを動かし、世界を動かし、ついにはGカップバストを動かしているのだぁ、と言えば哲学的(?)ではあるが、科学(?)ではない。いや、そんなのは科学的でも哲学的でもなくて、単なるエロ・エロ・トークだと言う人もいるかもしれないが、そういうことを言うヤカラは「純真でピュア〜」な目を持たない人に違いないのである。少なくとも、「なんて素晴らしいファンタジ〜なんだぁ」という位には言って欲しいのである。
 

　ただ、「ブランコを揺らす子供の動きとGカップバストを揺らす女性の動きは方向性が逆がである」ということは実は面白い考察ができるのである。前回、ブランコの動きを考えた時に、ブランコの効果的な漕ぎ方と方向性が逆の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合 」のシミュレーション計算をしてみた。その結果は、ブランコの振動がどんどん小さくなってしまったのであった。つまり、除振効果が働いてしまうのである。

　ということは、である。Gカップバスト(いやAAAカップでも同じであるが)を揺らす女性の動きは、実は揺らしているのではなくて、Gカップバストを揺らさないために最も効果的なのではないだろうか？Gカップバストが揺れ動いてしまってはオッパイ星人はともかく、本人はとても困るわけでそのために実は彼女らは「パラメータ(パラメトリック)励振」という物理現象・科学を応用しているのではないか、と想像してみるのもオツなものではないか、と私は思うのである。

　もちろん、ブランコの動きが実は結構複雑であるの以上にGカップバストの動きは複雑である。弾性・塑性・そして様々なブラジャ〜による拘束条件も解明しなければならないだろう。それは実にメンド〜な試みではあるが、きっといつか「純真でピュア〜な心」を持つ学生諸君がその謎を解明するに違いない。「天使のブラによる拘束条件とGカップバストのパラメトリック励振」なんていうタイトルの論文を近日中に目にすることができるに違いない、と私は夢見ているのであった。
 

■モンロー・ウォークの伝説X　

努力、天性、それともそれとも？

　世の中には二種類の人間がいる。「オッパイ星人」と「ヒップ星人」だ。いやもちろん、そんな風に人間を二種類に分けられるハズもなくて、これは口からデマカセの大ウソである。とはいえ、そんなホラを吹く根拠が必ずしも無いわけでもない。

　何故ならば、「オッパイ星人」シリーズの話を書くたびに、「胸のことなんかいいから、お尻のことを考えてるべきではないでしょうか？」というメールが届くのである。「私は揺れる（時には揺れない）胸よりも、プリプリ揺れるお尻にこそ断然目が引き寄せられます！」との意見も多いのだ。しかも、それが男性ばかりからというわけでもなくて、女性からも（もしかしたら、女性の方が多いかもしれない）そういったメールが届くのである。つまりは、男女を問わず、「お尻（ヒップ）星人= 」という異星人もまた地球上には生息しているらしいのである。

　これまで、本「できるかな?」ではそんな異星人達を識別すべく、日夜戦いを続けてきた。ぼくの地球を守るべく、そんな異星人達の特徴を見つけ出してきたのである。例えば、オッパイ星人であれば、「オッパイ星人」達は「揺れ動くオッパイ」に目を常にロックインさせているという特徴を利用し、「視線が妙に上下・左右に揺れ動くエイリアン」達を見つけ出してきた。ブレードランナー（アンドロイドは電気羊の夢を見るか？）でアンドロイドを見つけ出す主人公さながらに、私は戦い続けてきたのである。そして、その主人公と全く同じく、最終的には私までもオッパイ星人であるかのような気さえするほどだったのだ。

　私のことはさておき、それでは同じような戦法で「ヒップ星人」を識別できるものだろうか？「オッパイ星人」達は「揺れる胸の動き」に目をロックインさせていたが、「ヒップ星人」達はもちろん「揺れ動くヒップの動き」に目をロックインさせているハズだ。その揺れるくヒップの動きさえ調べてしまえば、「ヒップ星人」達特有の「奇妙に揺れ動く不自然な目」を見つけ出すことができるに違いないのである。結局は、揺れ動くヒップを調べさえすれば良いのである。

　「ヒップ星人」達の憧れる「揺れ動くお尻」と言えば、それはもちろんマリリン・モンローに違いない。何しろ、お尻フリフリの象徴たるモンロー・ウォークの開発者なのだ（多分）。お尻フリフリ＝マリリン・モンローと言っても良い位であるし、マリリン・モンローは「歩くお尻」と言っても良いくらいのハズなのである。

　というわけで、今回は何はともあれモンロー・ウォークを調べてみることにした。まずは、下の写真が「有名なお尻フリフリのモンローウォーク」の後姿である。
 

有名なお尻フリフリのモンローウォーク

　もちろん、静止画ではその揺れ動くヒップを実感できるわけもない。なので、モンロー・ウォークのバイブルとも言われているらしい映画「ナイアガラ」の1シーンを抜き出してみた。上がそのままの速度で再生したモンロー・ウォークで、下が奇数・偶数フィールド分離処理をして、半分の再生速度に変換したものである。

• 映画"Niagara"でのモンローウォーク（実速度再生）rm形式 92kB
• 映画"Niagara"でのモンローウォーク（フィールド分離処理をして、半分の速度で再生したもの）rm形式　178kB

　まずは下調べ、とモンロー・ウォークで検索をかけると、例えばこんな情報がそこらかしこに見つかるのである。

＜モンローウォーク／「ナイアガラ」ヒールの秘密＞

　スクリーンで見るモンローの魅力のひとつにモンローウォークがあります。ちょっと赤ちゃんみたいにヨチヨチ歩く感じ。それとボディのきれいなラインと豊かなバストがちょっと揺れるアンバランス感が魅力的な歩き方。「ナイアガラ」のワンシーンで、永遠とつづく道を歩いていく後姿のロングショットで、よく見るとハイヒールの高さが左右ちょっとちがうんです。どっちかが擦り減ってるとかじゃなくて、ちゃんと演出されているんだと思うんです。だから、靴の片方にだけ中敷をいれればモンローウォークの真似ができると思いますよ。

　そこで、目を皿にして、マリリン・モンローの揺れ動くお尻（じゃなかったヒール）に目をロックインさせてみたのではあるが、速いしブレるしで、全然判らないのである。そこで、その走査線の狭間に隠された真実を暴くべく、奇数フィールドと偶数フィールドを分離してみたりしたのではあるが、やっぱり判らないのである。ちなみに、下の画像がフィールド分離をした上での静止画例である。果たして、あなたは右と左のヒールの高さの違いが判るだろうか？右のヒールの方が左よりも短い、と断言できるだろうか？
 

映画"Niagara"でのモンローウォーク

　少なくともこの写真からは、私にはマリリン・モンローの右のヒールの高さが低いとは判断できない。まぁ、そもそも6mm程度の短さというのは、この動画から判断するのは無理なような気がしないでもない。

　そこで、他の判り易そうな画像をGoogleのImage Searchを使って調べてはみたが、やはり実際のところよく判らなかった。比較的判別しやすそうな下の写真を参考までに挙げておく。ぜひ、じっくり目をこらしてヒールの高さを判断してみてもらいたい。
 

マリリン・モンローのヒール

　ナイアガラなどのシーンを自分の目で眺めて、片方のヒールが短くカットしてあると判断した人は本当にいるのだろうか？巷にはモンローの片ヒールカットの伝説が溢れていて、「ナイアガラを見れば判る」とその伝説は言うのだけれど、本当のところその伝説を確かめた人がいるのだろうか？それはまさに幻の都市伝説なのではないだろうか？

　と、ここで終わってしまうといくら何でも私としても面白くないので、頭の整理も兼ねて、モンロー・ウォークの歩行模型を作ってみることにした。何しろ、映画の中にモンロー・ウォークのシーンがそれほどあるわけでもないし、それを眺めながらいろいろと考えるというわけにはいかないのである。ゆっくり動かしたり、色んな方向から眺めたりするには歩行模型を作るのが一番だろう。

　となれば、人間の歩行模型と言えばやはりコイツだろうというわけで、Poserの歩行シミュレーションを使って、ちょっと遊んでみることにした。モデルのヒールの高さ（実際には足底の厚さ）を変えてみた場合と、普通の場合とを比べてみるのである。左が普通？の場合で、右が片ハイヒールカット（マリリンモンローの場合とは反対であるが左足）の場合である。
 

Poserを使ったセクシーウォーク

普通？の場合

片ハイヒールカットの場合

　ふむふむ、確かに片ハイヒールカットの場合にはセクシー度がアップしているような気がする。なんと言うかプリップリップリップリッ…というか上品にオノマトペで言えば、プリップリップリップリッ…というか（全然変わってない）、

 しかし、片ハイヒールカットをすればセクシーさが増すと言っても、実際のところマリリン・モンローのハイヒールの高さが左右不ぞろいになっているかは確認できていないのである。このままでは、砂上の楼閣ならぬ砂上のモンローウォークなのである。もしかしたら、マリリン・モンローの歩き方が特にセクシー度がアップしているのは他の原因があるのでは無いだろうか？果たして、他に可能性は無いのだろうか？それを少し考えてみることにしたい。

　マリリン・モンローは比較的ぽっちゃり型であって、もともとお尻が少し大きいように私には思われる。言い換えれば、マリリン・モンローは安産型で骨盤が広いのである（多分）。腰の横幅が広いということは、どうしても左右の水平安定性に欠ける訳で、どうしても左右の腰の高さがユラユラとゆれてしまうのに違いないと私は思う。しかも、左右の腰自体の幅が長ければ、それが揺れたときの存在感もやはり大きいわけで、骨盤の長さが長くなると二つの独立した理由によりセクシー度がアップするハズなのである。ということは、骨盤の長さの二乗に比例してそのセクシー度はアップするハズなのだ。

　そこで、そんな安産型の女性が普通に歩いた場合の後姿を同じくPoserで眺めてみることにしよう。ちなみにここでは腰の幅を10%程普通の場合よりも広くしてみた。すなわち10%アップの安産型お尻の場合である。
 

普通の女性と安産型の女性が歩いたときの後姿の比較

普通？の場合

安産型の場合

　やはりお尻部分の横幅が10%アップしている分だけ揺れるお尻の存在感もアップしている。そして、さらにはお尻の動きが少し遅れているのか、こちらも方ヒールカットの場合と同じく、通常のフリッフリッフリッフリッ…に比べてセクシーなプリップリップリップリッ…のテイストを感じざるをえない。セクシー度は10%アップどころではなくて、30%くらいはアップしているような感覚さえ受けるのである。やはり、骨盤の長さの二乗に比例してそのセクシー度はアップする説は正しいに違いないのだ。

　この歩行模型ではないけれど、マリリン・モンローの場合もやはり骨盤が通常よりも広く、ただでさえ歩くときに左右の腰の高さ、いやはっきり言えば左右のお尻の高さが大きく変わりやすく、通常のフリッフリッフリッフリッ…がセクシーなプリップリップリップリッ…に変化したのではないだろうか？方ヒール説も面白いが、この単に安産説だってとても自然だと思う。

　ところで、もちろん先の片ハイヒールカット作戦をこの安産型プリップリップリップリッ…にさらに加えてやれば、もちろんもっと効果的なセクシー歩行になるわけで、それを実際に眺めて見たい！というわけでやってみたのが、次の比較である。何と言うか、普通の場合に対しても、さらには単なる片ハイヒールカットを行った場合よりも、安産型＋片ハイヒールカットでセクシー度がますますアップしているように思われる。通常のフリッフリッフリッフリッ…が見事なまでに官能的なプリップリップリップリッ…に昇華していることが判ることだろう。
 

安産型の女性がさらに片ハイヒールカットを行うと…？

普通？の場合

安産型の女性が さらに 片ハイヒールカット を行った場合

　本当のところ、今回映画や画像を眺めた範囲内では、マリリン・モンローの片ハイヒール伝説が本当なのかはよく判らなかった。「色々なことを考えている女性だった」というイメージにモンロー自身がしたかったり、あるいは周りがしたかったせいで生まれた伝説でないかとも思ったりする。もしかしたら、モンローは単にとっても安産型の女性だったせいで、あの歩き方になったのではないだろうか、とつまらなくも想像したりもする。

　とはいえ、私も浪花節の好きな日本人であるので、単なる偶然のお話でなくて「そこに隠された物語」のある方を気に入ってしまうタイプである。なので、モンローは生まれ持った安産型の体型を、つまりモデルや女優にはウィークポイントになりがちな欠点を、苦悶の末に片ハイヒール作戦によって長所へと変えて、あの有名なモンロー・ウォークを開発したとプロジェクトX（もういいかげん止めて欲しいと切に願っているのだが）風に考えておくことにしたいと思う。あぁ、何てキレイなまとめ方だろう…。

■オッパイ星人の力学 求む未来のヒロイン編　

タックルがおいっぱい。

　その苦しくも長いオッパイ星人達との死闘の歴史をちょっとばかり振り返ってみると、

1. オッパイ星人の力学 - 胸のヤング率編- (2000.06.29)
2. 続 オッパイ星人の力学 - 揺れる胸の動き編- (2000.07.02)
3. 続々オッパイ星人の力学 - 胸を揺さぶるパラメータ励振編-(2000.12.01)
4. オッパイ星人の力学 第四回- バスト曲線方程式編- (2001.01.13)
5. オッパイ星人の力学　仏の手にも煩悩編- 時速60kmの風はおっぱいと同じ感触か？ - (2001.01.27)
6. オッパイ星人の力学 あなたのオッパイ星人度編- 擬似オッパイに関するhiraxの関係式 - (2001.05.20)

　しかし、そんな死闘を続けているのは何も私だけではない。確かに、オッパイ星人をはじめこの地球上には異星人達があふれている。いや、もしかしたら、オッパイ星人と戦う私のような正義の味方はヤツらより数は少ないかもしれない。が、決してワタシは孤独な戦いを続けているわけではないのである。数少ない正義の味方達は日本中の各地で日夜戦い続けているのだ。というわけで、今回はそんな正義の味方達の戦いを、これまでのワタシの戦いと重ね合わせながら紹介してみたい、と思う。
 

　先日、素晴らしい論文（いや違う戦闘報告だ）を見つけた。それは日本人間工学会関西支部大会講演論文集Vol.2000Page. 112-115に掲載されている岡部氏らの「歩行に伴う乳房の振動分析」という報告である。内容は、

　着心地の良いブラジャーを設計するためには、乳房の形態を詳細に捉え、動的な挙動を明らかにする必要がある。そのため、歩行中の乳房の振動を、胸部土台の動きから分離・抽出し分析した。歩行中、乳房は複雑な振動を繰り返し、被験者により、また乳房の場所により異なる振動を示すことが判明した。特に、乳房の柔らかさによって振動の特性が大きく異なった。また、同じ乳房上でも柔らかさの違いが振幅と相関を示した。一方、場所が異なると振動に位相差が生じ、これが円運動・８の字型運動の発生につながることが判った。

岡部氏らによる「歩行に伴う乳房の振動分析」

　ワタシはこれまでオッパイ星人達と戦い続けてきた。しかし、その戦いの中で大きな悩みが一つだけあったのである。それは、ワタシが女性達を守るために戦っているにも関わらず、その女性達にワタシがどうも信用されていないフシがあることだった。「オレは味方だぁ」といくら力説しても、「ふぅ〜ん（どうだかねぇ）」と冷たい目でワタシを見る女性が多かったのである。いや、正直に言えばそうでない優しい眼差しを向けてくれる女性など皆無であったのだ。
 

　だから、、「オッパイ星人」達が目を常にロックインさせている「揺れ動くオッパイの動き」を調べようとしても、地球を守るための貴重な被験者になってくれる女性などいるわけもなく、ワタシの戦いはもっぱら計算上のモデルを主戦場としてきた。だから、そんなワタシの戦いを「机上の空論にすぎない」と言う方がいたり、「それって、単なるエッチな夢想ですか？」と言う人がいたり、はたまた「アナタは本当のオッパイを知らない」などと、ワタシは常に罵詈雑言を浴びせられてきたのである。「机の上がダメなら、どこの上なら良いんだぁ〜」とか、「想像力と好奇心が旺盛でどこが悪ぃ〜」とか、「余計なお世話だぁ〜」とか言いたくなるほど、世のため人のために戦い続ける正義の味方に世の中はとても冷たかったのである。

 そしてまた、FBIなどが犯罪者と戦う際によく用いる「おとり捜査」というような戦術も協力者がいないため、ワタシは遂行することができなかった。というわけで、「オッパイ星人」をワナにかけて退治しよう、なんていうことはとてもじゃないができなくて、ワタシの戦術はもっぱら専守防衛のみ、という状態だったのである。まるで、日本が誇るセルフ・ディフェンス・アーミーのような状態だったのだ。
 

　しかし、世の中にはそんなワタシのような情けない正義の味方だけではなくて、華やかな戦いを続けているグループもいるのであった。その良い例が先の素晴らしい論文（いや違う戦闘報告だ）を報告した岡部氏らのグループである。何しろ、彼らには年齢22〜23歳の成人女性12名が被験者として協力してくれているのである。仮面ライダーでさえ味方の女性はタックル一人しかいなかったし、五人もいるゴレンジャーの中でさえ仲間の女性はモモレンジャーただ一人しかいなかった。なのに、彼らには12人もの女性の協力者がいるのである。素晴らしくゴージャスなのである。人数で言えば、まるで「モーニング娘。」程のタックルがいるのだ。

　しかも、かの戦闘報告にはより詳細なタックル達の紹介文までついており、それによれば

• Bカップの65 1人
• Bカップの70 4人
• Cカップの65 1人
• Cカップの70 4人
• Cカップの75 1人
• Dカップの75 1人

　ちなみに、そのオッパイの柔らかさ測定に用いられた測定器は日本電産シンポ（株）製のデジタルフォースゲージである。　…ワタシも硬さの測定をたまに仕事でするので、フォースゲージを使うこともあるのだけれど、これまでこんな測定はしたことがない…。う、うらやましい。
 

デジタルフォースゲージ
( http://www.shimpo.com/shimpo/is/dfg/dfg.htm )

押付力、引張力など各種「力」の計測に対応 計測範囲 ２Ｎ用〜４９０Ｎ用までシリーズ化  …

　このフォースゲージを製造している日本電産シンポも - 各種「力」の計測に対応-と書いてみても、まさかオッパイの弾力の計測に使われるとは思うまい。まさか、異星人「オッパイ星人」との正義の戦いの武器に使われるとは思わなかっただろう。きっと、それを知れば日本電産シンポも正義の誇りに奮い立つハズなのである。

　もちろん、先の素晴らしい論文（いや違う戦闘報告だ）には、その正義の武器デジタルフォースゲージを用いた「オッパイの弾力の実測データ」も掲載されており、それが下のグラフだ。
 

オッパイの弾力の実測データ　　う、うらやましい。

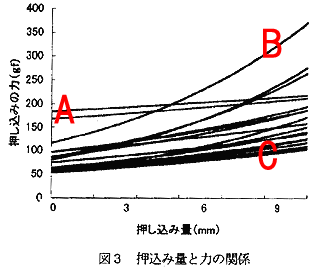（赤文字はワタシが記入）

　横軸がフォースゲージをオッパイへ押し付ける「押し込み量」で、縦軸はその押し込んだ指プローブをオッパイが「押し返す力」である。このグラフから判るように、オッパイを押し込めば押し込むほど押し返す弾力は強くなるわけだ。もちろん、どんどん押し込めば土台としての肋骨があるハズなわけで、いずれ硬い肋骨にぶつかって「押し返す力」は限りなく大きくなってしまうハズである。その良い例がデータBであって、1cmも指プローブを押し込めば土台としての肋骨に突き当たっているかのようである。

　しかし、片やデータAやCのようにその程度押し込んだだけではまだまだ押し返す弾力が強くならない、言い換えれば懐の深さ（それを単に巨乳といってはイケナイ）を感じさせるものも存在するのである。このようなデータを眺めるとき、我々は何が何でも構造解析をしてみたい、と思うのは至極当然のことであろう。
 

　また、面白いことに例えば前回考察した「走る車の窓から出した掌が受ける力とオッパイ一個あたりの重さ(g)を重ね合わせたグラフ」などとこのグラフを並べてみると、まぁまぁ良い感じで力のオーダーが一致していることがわかる。つまり、単なる前回考察したような数値、ワタシが苦しくも続けてきた戦い、は必ずしも「机上の空論」ではなくて、年齢22〜23歳の成人女性12人のタックル達の貴重なデータと割合良い一致し、無駄ではなかったことが確認できるのである。また、ワタシも彼らも「グラム重」を単位として採用していることも確認して頂きたい。
 

走る車の窓から出した掌が受ける力 ( g重換算 ) 
胸のカップ数とオッパイ一個あたりの重さ(g) 
を重ね合わせたもの

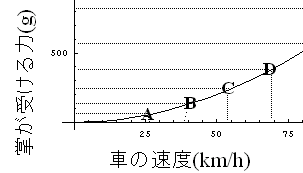　そしてまた、彼らはタイトルにもある通り歩行時にタックル達のオッパイの揺れるさまも実測しており、ワタシが続オッパイ星人の力学 - 揺れる胸の動き編 -などで計算し続けてきた歩行時の女性のオッパイの動きとも比較することができるのである。

　例えば、その二つを並べたものが下の二つのグラフである。左が実測されたオッパイの揺れるさまであり、右がワタシが計算したGカップバストの女性のオッパイの動きである。
 

実測されたオッパイの揺れるさま（左）、
と
「机上の空論」のGカップバストを揺らす女性のオッパイの動き（右）

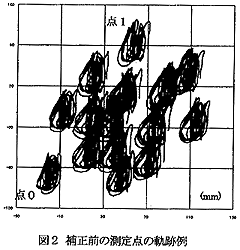Gカップバストを揺らす女性のオッパイの動き

　これらを並べてみると、実測値の方が比較的単純な動きであるのに対して、右側のワタシの計算値の方はずいぶんと複雑になっているが、これはワタシの考えではカップの大きさの違いとオッパイの振動の減衰の仕方が異なるせいだと考えている。比較的小ぶりなバストでは単純な動きですむのであるが、ワタシの試算ではバストが大きくなると動きは急激に複雑になるのである。また、ワタシの計算はオッパイを比較的単純な弾性体として取り扱っているが、本来柔らかいオッパイはそういうものではなくて、オッパイ星人の力学第四回 - バスト曲線方程式編-で挑戦し始めたような水風船モデルで取り扱い、さらにその中でエネルギーの減衰も組み込む必要があると思うのである。

　次に、歩く速さを変えたときの実測値と計算値を比較してみる。まずはゆっくり歩いた時のオッパイの振動のようすである。なお、実測値の方は水平方向と鉛直方向の揺れとが分離され表示されている。
 

ゆっくり歩いた時の乳房の振動（実測値）（左）と、「机上の空論」のGカップバストの軌跡（右）

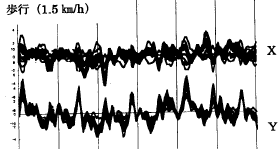Gカップバストの軌跡 (1秒で2歩の場合)  横軸 : 左右(cm)  縦軸 : 高さ(cm)

　これを眺めると、実測値、計算値のいずれにおいても水平方向と鉛直方向にそれほど相関が無い複雑な動きをしていることがわかるだろう。何と言うか、言葉にはできないがアッチコッチアッチコッチぐるんぐるんな状態なのである。

　それに対して、速く歩いた場合には結構単純な揺れ方になってくる。それを示したのが下のグラフである。実測値では水平方向と鉛直方向の動きが比較的相関が高そうなことが見て取れるし、右の計算値では一目瞭然ユッサユッサと単純かつキレイな動きになっているのである。
 

速く歩いた時の乳房の振動（実測値）（左）と、「机上の空論」のGカップバストの軌跡（右）

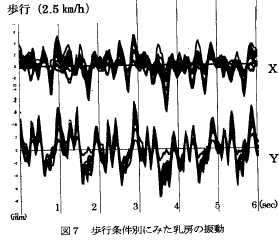Gカップバストの軌跡 (1秒で6歩の場合)  横軸 : 左右(cm)  縦軸 : 高さ(cm)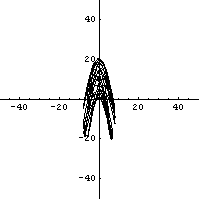

　このように素晴らしい実測データとワタシのこれまでの戦いを比較してくると、「ワタシの戦いも必ずしもムダではなかった」と思えてくるから不思議である。そして、見たいの地球を守るためにワタシはさらに戦い続けることを誓うのである。

　しかし、やはり実測があっての計算である。オッパイ星人を始めとする異星人達の攻撃にさらされている地球を確実に守るためには、ワタシのこれまでの「専守防衛」作戦だけではなくてもっと攻撃的な布陣や戦略を活用したいところだ。そのためには、ワタシと一緒に未来の地球を守るタックル達の結集を強く望む（自衛隊のポスター風に）次第であると一応書いておいて、今回の反省会を終了したいと思う。
  

■今日見た景色 朝に光る穂　

　これが揺れて、きらめいて、とてもきれい。 （リンク）