2000-11-13[n年前へ]
■WEBサイトでMONOPOLY 
これも一つのリンクページ
先日、ZDNet Japanを眺めていると面白い記事があった。ボードゲームの「モノポリー」にドットコム版ができたというのである。
- 「モノポリー」にドットコム版( http://www.zdnet.co.jp/news/0011/06/monopoly.html )
- Monopoly ( http://www.monopoly.com/dotcom/dotcom.html)
ところで、「モノポリー」というのは実に酷なゲームである。お金を奪い合い、お金が無くなったプレイヤーは容赦なく破産させられるのである。金が乏しくなってきて、もう他人に払うお金の持ち合わせなんか全然無くて「オレは別にここでこのままじっとしていたいんだぁ。」と言っても、そんなことは許されず強制的にサイコロを振らされるのである。そして、勝手に旅をさせられてわけのわからない場所に移動させられたかと思うと、「あっ、そこオレの場所。ホテルがあるから300ドル払ってね。」となるのだ。オレはただこの道ばたでじっとしていたいだけなのに、何でサイコロを振らされて、しかもオマエのホテルに泊まらアカンねん!と泣き叫びたくなるのである。オレは金なんか持ってないから、そんなグルグル高そうな場所を旅する余裕なんかないの!と言っても他人はただ笑うのみなのだ。
ヒドイ話である。ほとんど、「金なんか別にいらないよ。」と言っているのに勝手に金を貸して、しかもバブルが崩壊したら強引に金を取り立てはじめるどこぞの国の銀行のノリである。
「7並べ」くらいでも泣く子供(それは昔の私。親戚が集まるとよくこの話になり、今でも泣きたくなる。)もいるというのに、「モノポリー」なんかやった日にはもう子供が人間不信になることは間違いない。ハッキリ言って、「モノポリー」で涙をこぼして写真を撮られた大学生を私は何人も知っている。イナかっぺ大将の「風大左エ門」のように両目からボヨ〜んと涙をこぼす大学生の写真だって私の手元にはあるくらいだ。
そう言う感じで「モノポリー」はあまりにも子供達には酷なゲームなので、純粋で(少なくとも勝負には)可哀想な子供達と「モノポリー」をやるときには、銀行係になった私はいつも救済のためのお金をばらまいてしまう。つまり、お金が無くなりそうな子供が出そうになると、「日本銀行から、ボウナスが出たぞぉ!」と言いながら、みんなにお金をバラまいてしまうのである。確かに、泣きそうな子供はいなくなるではあるが、何故かそのあとオソロシイほどのインフレが襲ってくるのである。先ほど、どこぞの国の銀行に皮肉を書いてしまったが、少なくとも、私にはツブれそうな会社にお金をバラまくどこぞの国の大蔵省を怒る資格は無さそうである。子供達と「モノポリー」をやるときには、私も全く同じコトをしているのである。
ところで、「モノポリー = MONOPOLY」はといえば市場(ゲーム上では場所だけど)独占をして、お金をもうけるゲームである。WEBサイトの世界でも同じように「独占」という状況はあって、
で書いたように、「インターネットのほとんどのアクセスというものは、ごく少数の特定のサイトへのもの」なのである。ごく少数の大手サイトによってほとんどのアクセス数は独占されているのである。まだ普通の商売であれば独占禁止法( Antitrust [Antimonopoly] Law)があるのだが、WEBサイトへのアクセスではそんな独占禁止法なんかあるわけがない。なので、WEBサイトを冠するドットコム企業の独占を狙う「モノポリー」ドットコム版というのはとても当たり前で自然なのである。
というわけで、「モノポリー」ドットコム版を私はとても面白く感じたので、そのHIRAX.NETEditionを作ってみることにした。つまりは、ただの私のリンクページなのであるがまぁちょっとデザイン的に変わっていて面白いのと思うのは私だけだろうか?
 |
それでは、振り出しからこれらのサイト達の紹介をしていきたいと思う。まずは、WEBでショッピングをしよう。というわけで、ぷらっとホームと秋月電子通商である。ここで電子部品や面白グッズ・ソフトを揃えたら、お次は私の巡回コースの基本である技術系サイトである。今日の必ずトクする一言・Fast& First・突撃実験室と廻ってみよう。
さて、牢獄を眺めながら次は情報サイトを廻ってみよう。というわけで、お笑いパソコン日誌・MAQ?MAK?MAC!・ZDNetNEWSだ。最後のヤツだけ個人サイトではないが、今回の情報源でもあるし一応入れてみた。
そして、お次は続・技術系(LabVIEW・電子工作編)というわけで、LabVIEWinfo sharing・えるむ・CyberWorkShopである。最初のは同業ライバル社の方というところに親近感を持っていたりするのだ。CyberWorkShopはもう永久に更新が無さそうなところがとても残念である。
そして、パーキングを経由して「読み物サイト」へ行こう。寂しいことに更新が停止したままのちゃろん日記(仮)・もう本気で感情移入せざるを得ない我妻との闘争・そしてこの我妻サイトの弟子サイトでもある乳から息子に宛てた手紙である。
そして、次は「理系文系ごっちゃまぜ読み物」である。まずは、本来こんなところに登場する資格はないのだが、本人のサイトということで強引に登場させた「できるかな?」・「僕が作る僕の可能性」という言葉も私は大好きなボクテレビ・そして、トンデモ系の推理を作るのは大変だろうなぁとつくづく思わざるをえないHMRだ。
そして、最後のコーナーを曲がって次は時事エッセイ日記だ。まずは、ワイドショーの奴隷・麗美のぷらぷら日記である。理系風ワイドショーという感じが面白いところである。そして、何故か場所の関係でここに配置されたデザインの一つの理想たるげんれい工房・言霊参上(ことだまさんじょう)だ。
そして、最後の二つ、つまりゲームの「モノポリー」で言えばここに止まったら大変だぁ、という場所はもちろんWEB噂の真相と2ちゃんねるである。ここで自分と関係する情報などを見かけてしまうと、実際の所結構ビックリするものである。
もちろん、私の巡回サイトといいうのはここに挙げたものだけでなくて、こっそり覗いているサイトは多々あるわけだ。しかし、そういうところはとりあえず、秘密である。
さて、本当の「モノポリー」ならともかく、今回のWEBサイト達はいくら泊まろうがお金を取られたりはしない。もちろん、一部のサイトでは広告くらいは表示されるかもしれないが、間違っても「あっ、ここオレのサイト。ドメイン維持のために300ドル払ってね。」ということはないハズである。だけど、時間だけはタップリ奪われてしまうかもしれないから、そのつもりで。
2000-11-26[n年前へ]
■ブランコの中の∞(無限大) 
なんで一体漕げるのだろう?
公園のブランコというのは、何故かとても不思議な雰囲気を持っている。ホントにうるさいくてたまらないくらいのガキんちょ達が、アクロバットのようなスゴイ技を見せていたりする。それは、まるで上海雑伎団を見ているような気分になる。小さな子がなかなかブランコが漕げず、ブランコの上で宇宙遊泳のように四苦八苦しているのを見ているのも思わず笑ってしまうくらいに可愛らしいものだ。もちろん、そこは子供の領分というだけではなくて、黒沢明の「生きる」の主人公がしていたように「大人がブランコに座って揺れていたり」すると、思わずその人の陰に隠れている物語を想像したりしてしまう。ブランコの周りというのはそんな不思議な雰囲気を持っているのだ。
やたらにブランコを漕ぐのが上手いガキんちょもいる一方で、全然ブランコを漕げず四苦八苦する子供もいる。ブランコを漕ぐコツを覚えるのもなかなか大変そうである。考えてみれば、ブランコは一体どういう風に漕ぐものなのだろう?口で上手く説明できる人がいるだろうか?
それに、そもそも私たちはブランコを何故漕ぐことができているのだろう?
いったい、いつから疑問に思うことをやめてしまったのでしょうか? いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか?という手紙で始まるのは加納朋子の「ななつのこ」だが、「何故、リンゴは落ちるのかという謎」と同じく、「ブランコの漕ぎ方の謎」だってとても不思議だ。いつも目にする公園のブランコを、私たちは一体どうやって漕ぐことができているのだろう?
いつだって、どこでだって、謎はすぐ近くにあったのです。
何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。
もちろん、「何でブランコの漕ぎ方が不思議なのさ?」と言う人も多いだろう。その中には理路整然とブランコの漕ぎ方を説明してくれる人もいるだろう。そして、「特にブランコの漕ぎ方をじっくり考えたことなんかないもんね」という人も多いに違いない(私だけかもしれないが)。そこで、まずは「ブランコの不思議」を簡単に書いてみることにしよう。
次の図は「ブランコを漕いでる子供」である。
 |
この子供が何もせず立っているだけ(あるいは座っているだけ)だったら、どうなるだろうか?それはもちろん、単なる振り子と同じくようにブランコは動く。もしも色々な摩擦がなければ、まったく同じように動き続けるだけだし、摩擦力があればブランコの動きはただ減衰していくだけである。つまり、子供が何もしなければ、ブランコの動きは「遅く・小さく」なることはあっても、ブランコが「速く・大きく」なることはないのである。
だからブランコを速くするためには、「ブランコに乗ってる子供がブランコを漕がなければならない」わけであるが、ブランコに乗ってる子供は一体どんなことができるだろうか?
次に示す図は「ブランコに乗ってる子供を中心にとった座標軸」を描いてみたものだ。この図の中で直交する二つの軸を描いてある。つまり、
- ブランコの動きの中心を向いている軸A
- 軸Aに直交する、つまりブランコの進行方向(あるいはその逆方向)を向いている軸B
 |
ところが、実は「ブランコに乗ってる子供」はこの二つの軸の内の片方、軸Aに対しての動きしかできない。何故なら、軸B方向に対しては「ブランコに乗ってる子供」動きの支えになるモノが全然無い。だから、ツルツル滑る氷の上では全然動けないのと同じく、「ブランコに乗ってる子供」はその方向には動けないのである。もし子供がその方向に動こうとして体を動かしたりしても、結局子供の重心はその方向には全然動かないのだ。
それに対して、ブランコの動きの中心を向いている軸A方向に対してはブランコの鎖も座っている(あるいは立っている)板が支えになるわけで、その方向に対しては「ブランコに乗ってる子供」は動くことができる。
というわけで、ブランコの上では「ブランコの動きの中心を向いている軸A」方向にしか動けないわけであるが、その方向というのはブランコの進行方向に対しては直交している。つまり、ブランコを漕ぐためには、「ブランコの進行方向に対して直交している方向に動く」しかないことになる。
ここまで書くと、ブランコの不思議が判るハズだ。ブランコを漕ぐ、つまりブランコを軸B方向の速度を上げたいのに、我々は「軸Bに対して直交している方向に動く」ことしかできないのである。一体何故、軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増すのだろうか? この謎「ブランコの不思議」を、ゆっくり考えてみることにしよう。
まずは、ブランコに乗ってる子供が立ち上がったりして、「ブランコの動きの中心を向いている軸A」方向に動いた場合、何が起きるだろうか?
 |
「ブランコの動きの中心を向いている軸A」方向に動くと、ブランコの鎖の長さが短くなることと同じである。すると、回転しているブランコの鎖が短くなるわけで、そうするとブランコの速度は速くなる。何故なら、角運動量が保存されるからである。ちょうど、スケートのフィギア競技の選手が回転中に伸ばしていた手を縮めると回転数が早くなるのと同じだ。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの半分だけ(とんでもない身長の子供だ!)上がれば、ブランコの速度はもとの速度の倍になるのである!
ということは、少なくともこの瞬間は「軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増す」わけであるが、これでブランコの漕ぎ方を納得するにはまだまだ早いのである。確かに、「ブランコの動きの中心を向いている軸A方向に動く」とブランコの速度は増すわけであるが、それはその瞬間だけである。ブランコの上で「立ち上がり続ける」なんてことはできないわけで、速度が増し続けるわけではないのである。
もしも、「もう一度ブランコの上で立ち上がるために、すぐに低い姿勢に一旦戻ったり」したら大変だ。ブランコの鎖の長さが長くなるのだから、今度はブランコの速度は遅くなってしまうのである。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの二倍だけ(つまりさっき立ち上がった逆の動きである)下がれば、ブランコの速度はもとの速度の1/2になってしまうのだ!
これでは、結局さっきの速度が二倍になったことは帳消しになってしまう。つまり、「単純に」角運動量の保存を考えるだけではブランコの速度を(長い間にわたって)早くしていくことはできないわけだ。
このままでは、「ブランコを漕ぐことなんか不可能である」という結論が出てしまいそうになるが、ブランコを漕いでる子供達はイッパイいるわけで、そんな結論を受け入れるわけにはいかない。彼らがみんな超能力でブランコを漕いでいるわけもないのである。まだまだ見落としていることがあるので、ブランコの不思議の謎が解けないだけのハズなのだ。
そこで、ちょっと考えてみると「とんでもなく単純なこと」を見落としていたことに気付いた。それは、「タイミング」である。例えば、ブランコの速度がずっと同じであるすると、
- 初期のブランコの速度 = 10
- 重心位置を高くして 10 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- 重心位置を低くして 10 X 1/2 = 10 (何てこったい、速度が半分になっちまったか!)
- 初期のブランコの速度 = 10
- 重心位置を高くして 0 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- そのあとブランコの速度 = 0
- 重心位置を低くして 0 X 1/2 = 0 (0が0になっても全然変わってないもんね!ヘヘン!)
人生何事もタイミングが重要である。失恋した男性や女性にタイミングをわきまえた「恋のハイエナ」達が寄ってくるのと同じく、またお金に困っていると何故かサラ金の広告が目の前にチラチラするのと同じく、ブランコを漕ぐにはやはりタイミングが重要なのだ。
なるほど、考えがまとまってきた。このイキオイでそのまま「ブランコの理想の漕ぎ方」まで考えてしまおう。
まず、「重心位置を高くしてブランコの速度早くする」にはできるだけ速度が速い瞬間に行うのが良いだろう。倍率が確定している賭なのだから、元金はあればあるほどおトクである。1万円×2=二万円では1万円しかもうからないが、一千万円×2=二千万円では一千万ももうかるのだ。ブランコの速度が速い瞬間に立ち上がれば、一番おトクに速度を増すことができるのである。
もちろん、ブランコの速度が速い瞬間といえば、明らかにブランコが一番下にきた瞬間である。つまり、ブランコが一番下にきた瞬間に立ち上がれば「一番おトクに速度を増すことができる」わけだ。しかも、その瞬間は鉛直に重心を持ち上げることになる。つまり、位置エネルギーを効果的に増加させることができるわけだ。結局、この時に増加させた位置エネルギーは後で、運動エネルギーに変換されるわけで、結局これがブランコの運動の源となるのである。
そして、「次にもう一度立ち上がるために一旦低い姿勢に戻る瞬間」=「速度が遅くなる瞬間」はブランコが停止しているときであれば何の問題もない。ブランコはもともと止まっているんだから、その速度が何分の一になったって全然気にしないもんね!となるわけだ。そのタイミング= ブランコが止まる瞬間といえば、もちろんブランコが最高地点まで上がった瞬間である。つまり、ブランコが一番上にいった瞬間に低い姿勢に戻れば全く減速無しに次の加速に備えることができるわけである。しかも、その時には実は運動エネルギーを位置エネルギーに変えることで、隠し財産にしているわけで、もう汚い政治家のマネーロンダリングのような見事な方法なわけだ。
というわけで、
- ブランコが下に来たときに(立ってる場合は)足を伸ばして立ち上がったり、(座ってる場合は)足を曲げたりすることにより高い位置に重心を持ってきて(しかも、重力に逆らって重心を上げるため位置エネルギーが増加する)
- ブランコが上に行ったときにその姿勢を元に戻す
それでは、確認のためにそのやり方で本当にブランコが漕げるのかどうか、シミュレーション計算を行ってみた。ブランコの動きは振り子運動だが、振れ幅がとても大きいので、cosx≒xというような近似をする単振動としての扱いはできない。そこで、楕円積分の計算を行わなければならない。が、私が自分の力でできるかどうかはともかく、そこはMathematicaに解かせればイッパツである。もう、驚くくらい簡単なのである。自分の力で解いていないところが、実に悲しい現実ではあるが、それが現実なのだからしょうがない。
というわけで、ブランコの動きのシミュレーションをしてみた結果が次のグラフである。「ブランコに乗ってる子供」の漕ぎ方としては、以下の三つ
- 何もしない場合
- ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合
- ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合
 → ブランコの動きはず〜と変わらない |
ブランコが上にきたあたりで座り込んだ場合  → ブランコの動きはどんどん大きくなる 「やったぜ、これが理想の漕ぎ方だぁ。」 |
ブランコが上にきたあたりで立ち上がった場合  → ブランコの動きはどんどん小さくなる 「なんてこったい、遅くなっちまったぁ。」 |
この結果から、ちゃんと1.の「何もしない場合」は「ブランコの動きはず〜と変わらない」し、理想の漕ぎ方であるハズの2.の「ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合」は「ブランコの動きはどんどん大きくなる」し、最悪の漕ぎ方であるハズの3.の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合」には「ブランコの動きは逆にどんどん小さくなってしまう」ことがわかる。というわけで、今回考えた「ブランコの不思議= 漕ぎ方」はシミュレーション計算結果からも確かめることができたわけだ。
ところで、こういったタイミングを考えながらパラメーターを変えることで動きを大きくしたりすることは「パラメータ励振」と呼ばれる。ブランコの漕ぎ方はその「パラメータ励振」の応用のひとつである。「何故、リンゴは落ちるのかという謎」には重力という基本的な物理現象が隠されていたが、それと同じく、「ブランコの漕ぎ方の謎」にも「パラメータ励振」という物理現象が隠されているのだ。次回以降も、この「パラメータ励振」を手がかりにいくつかの「身近な謎」に迫ってみたい、と思うのである。
さて、公園でブランコを漕ぎまくる子供をもし見かけたならば、ぜひ横から子供の動きを見てやってもらいたい。きっと、その揺れ動くブランコの中にはこんな∞(無限大)の形が見えるハズだ。天まで上ろうとする「ブランコの秘密」はその「ブランコの中の∞(無限大)」に隠されていたのである。子供も含めて人間の可能性は∞(無限大)だと私は思うが、ブランコの揺れる動きから、そんなことを考えてみるのも少し面白いのではないだろうか? それとも、ちょっと考え過ぎかな。
2001-08-23[n年前へ]
■あの小判で何が買えたの? 
「夏休みの自由研究」図書館で江戸時代の物価を調べてみた
夏休みも終り、また忙しい生活が始まった。忙しい生活をしていると、「あぁ昔のノンビリとした時代、例えば江戸時代に戻りた〜い」なんて思ってしまう。江戸時代のお気楽な町人かなんかに生まれ変わって、ぼぉ〜っとしてみたり、祭りや火事に興奮してみたり、たまには働いてみたり、そして時には近所の町娘と恋なんかして過ごしてみたりしたいなぁ、と思ってみたりするのである。それに、江戸時代と言えば大昔なのだから、きっと物価はものすごく安いに違いないのである。平均給料がいくらだか知らないが、きっと色々なモノが安く買えるに違いないのだ。
といっても、私は歴史にはとっても疎い(いや違った、「歴史も」だ)ので、本当のところ江戸時代がそんなノンビリとした時代だったかどうかは知らない。まぁ、知らないからこそ、適当にこんな風に楽観的に思ってしまったりするのである。
しかし、世の中には私のような「歴史知らず人間」だけでなくて、「歩く歴史」人間のような方々も多いのである。いや、こう書くといきなり誤解されてしまいそうだ。私は別に「歩く化石」人間が多いとか、「踊るシーラカンス」人間が多いとか言いたいわけではないのである。旧人類が満ち溢れていると言いたいわけではないのである。私は、単に世の中には「歴史大好き」人間が多い、ということを言いたいだけなのだ。そう、例えば歴史大好き人間、例えば時代劇大好き人間(*1)とか幕末野郎(*2)とか戦国野郎(*3)などはきっと誰の周りにもいるハズなのである。
(*1) 古くは「杉さまぁぁ〜」と黄色い声を上げる杉良太郎大好き・時代劇大好きおばちゃん(いや、違ったおねえさん…)、など。そんな「歩く歴史」人間の方々は私を、「江戸時代はきっと色々なモノが安く買えるんだ〜。いいなぁ〜。」などと無知にも憧れたりする素直な私を、必ずやバカにするに違いない。いや、バカにされるのは構わないのであるが、そうなると、そんな自分をちょっと情けなく思ってしまう。
(*2) 坂本竜馬に自分を例える武田鉄也、など。
(*3) 会社から外へ飛び出し、その退社時に「江戸城」という本を後輩に渡して行くようなカッコイイ人、など。
そこで、今回夏休みのぼ〜っとした気分からのリハビリも兼ねて、江戸時代と現代の物価について調べてみることにした。そして、夏休み過ぎの私が夢想する「江戸時代への憧れ」がトンチンカンなものなのか、あるいはそうでないのかを調べてみたい、と思う。つまり、今回は単に「夏休みの自由研究 図書館で江戸時代の物価を調べてみた」ということなのである。そして、「江戸時代はきっと色々なモノが安く買えるんだ〜。いいなぁ〜。」の是非を確かめることにしよう。
とはいっても、じゃぁ、すぐに江戸時代の物価と現代の物価を比べよう、といきなり始めるわけにはいかないだろう。なんと言っても、江戸時代は実に長い。何しろ、江戸時代と一言で言っても、260年もあるのだ。その長い江戸時代の間にお金の価値(物価)がものすごく変化していたとしたら、一体どれが「平均的」江戸時代なのか判らない。
そこで、まずは図書館に行って、「江戸物価辞典」を片手に江戸時代の間に米の価格がどの程度変化していたのかをグラフにしてみた。江戸時代の間に物価がどの程度変化していたかを見てみるわけだ。もちろん、何をもって物価の上昇具合が緩やかなのかあるいは急なのか、という基準が必要なわけで、第二次大戦後の米価格の変化も同じように示してみた。
 |
上のグラフを眺めてみると、江戸時代(幕末期は除く)は緩やかな物価上昇は見られるが、それはごくごく緩やかなものであることが判る。何しろ200年も経っても、たかだか二倍程度にしか上昇していないのである。第二次大戦後の(すなわち、たった50年程度の間の)物価上昇に比べれば、もう物価上昇はほとんど無いといっても良いくらいである。少なくとも人生50年というような時間尺度で眺める限りは物価はほとんど変化していないのである。私の記憶(とても曖昧…)があるたった25年足らずの間に、駄菓子の価格がほとんど二倍(ガリガリ君を除く)になっているのとは大違いなのだ。ということは、少なくとも江戸時代の中期辺りの物価を眺めてみれば、それを「江戸時代」と言ってしまっても良さそうに思える。そこで、
の江戸時代中期の色々なモノの価格をグラフにして並べてみる。また、それらのモノが西暦2001年の現在、何円くらいであるかを私の主観によって判断し、同じようにグラフにしよう。そして、それぞれを比較して、- 今の方が安いモノ
- 昔の方が安かったモノ
とはいえ、もちろん江戸時代にあったが現在はもうほとんど存在しないというようなものも多い。そこで、そういうものは現在における相当品で、例えば
- 富くじ → 宝くじ
- 吉原高級遊女 → 銀座の高級?クラブの基本料金
- 町駕籠 → タクシーの初乗り料金
- 夜なきソバ → 近所のチャルメラ・ラーメン
- 絵本 → 写真集
- 貸し本 → レンタルビデオ
- 夜鷹 → ○×△■
また、モノの価格だけでなく「収入」の基準もやはり必要なわけで、それに対しては大工日当を用いた。つまり、収入の基準との大工日当に対して、色々なモノがいくらであるかを、江戸時代と現在とで比べてみることになる。というわけで、そのグラフが以下である。
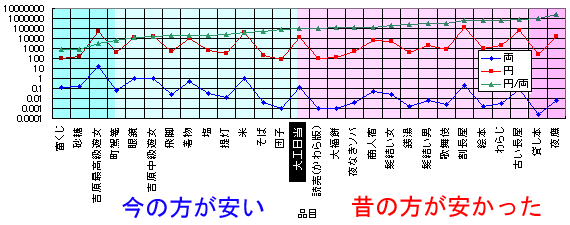 |
このグラフを見ると、例えば大工日当を基準にすると、一両はほぼ十万円に相当することが判る。また、砂糖などは今のほうが江戸時代よりもよっぽど安い。だから、砂糖を基準にすれば、一両は千円にしかならない。逆に夜鷹を基準にしてしまうと、何と一両はおよそ百万円に相当するのである。それほどに江戸時代の夜鷹は安かったのだろう。大変な話だ…。
砂糖も含め、眼鏡とか町駕籠(タクシー)とか飛脚(宅急便)とか提灯(懐中電灯)とかの、いわゆる科学の力を有効活用したものは当然現代の方が安い。そして、わらじとか歌舞伎とかの現代においては希少価値の高いものは江戸時代の方が安かったのも当然である。じゃぁ、吉原高級遊女(銀座の高級?クラブの基本料金)と吉原中級遊女(銀座の大衆クラブ)の価格の違いはどう説明するのかいう疑問も当然湧いてくるわけではあるが、そういう話はどうでも良いのだ。
何はともあれ、タクシー(町駕籠)に乗って銀座のクラブ(吉原高級遊女)に遊びに行くのが大好きな人、しかも眼鏡をかけてて、甘いもの(砂糖)が大好きなんて人には江戸時代はどうも合いそうにない。そんな人たちはすごくお金持ちでないと、江戸時代はかなりツライ時代のようである。そんな人達は、江戸時代よりも2001年現在の方が幸せに違いない。そんな輩には江戸時代はマッチしないハズなのである(根拠薄弱)。
しかし、広い風呂(銭湯)が好きで、夜のチャルメラ・ラーメン(夜鳴きソバ)にロマンを感じ、写真集(絵本)が欲しいけど高くて買えないワタシのような人間にはやはり江戸時代がジャストフィットするに違いないのだ。チープにお気楽に生活できるかもしれないのである。やはり、「江戸時代はきっと色々なモノが安く買えるんだ〜。いいなぁ〜。」は合っていたのである(ウソ)。
よっしゃぁ、私に合う時代はやっぱり江戸時代なのだぁ、とここまでは思ったのだが、もう少し私の生活パターンを考慮して吟味し調べてみると(調べなくても判るだろうが…)、江戸時代には発泡酒はもちろんビールは日本では一般的ではなかったのである。これでは、ビール(だけどお金が無いから発泡酒に変わったが)大好き人間の私としては致命的にマズイのであった…。う〜ん、う〜ん、ちょっと残念なんだけどだなぁ…。
2001-09-04[n年前へ]
■hpがCompaq買収 
大丈夫かなぁ、hp。特許であれだけお金払って…、カラー関係の技術者が逃げ出してて…、そのhpと一蓮托生状態の…(以下省略)
2001-09-10[n年前へ]
■今日の書評 
今日の朝日新聞夕刊。萩原博子、中沢孝夫、童門冬ニの三氏の書評。中沢氏の文章に納得し、童門氏の文章を思わず鼻でフフンと笑う。ちなみに、題材は「ファーストフードが世界を食いつくす」「ニッポンのコメ」「プロジェクトXリーダーたちの言葉」
「学資が安いという理由で東京大学工学部に入学」とか「男が惚れる男」なんて言葉が出てくるのでびっくりだ。お金があったらどの大学に入りたかったのだろうか。女が惚れるのとどう格が違うのだろうか。 by 中沢孝夫。