2000-11-26[n年前へ]
■ブランコの中の∞(無限大) 
なんで一体漕げるのだろう?
公園のブランコというのは、何故かとても不思議な雰囲気を持っている。ホントにうるさいくてたまらないくらいのガキんちょ達が、アクロバットのようなスゴイ技を見せていたりする。それは、まるで上海雑伎団を見ているような気分になる。小さな子がなかなかブランコが漕げず、ブランコの上で宇宙遊泳のように四苦八苦しているのを見ているのも思わず笑ってしまうくらいに可愛らしいものだ。もちろん、そこは子供の領分というだけではなくて、黒沢明の「生きる」の主人公がしていたように「大人がブランコに座って揺れていたり」すると、思わずその人の陰に隠れている物語を想像したりしてしまう。ブランコの周りというのはそんな不思議な雰囲気を持っているのだ。
やたらにブランコを漕ぐのが上手いガキんちょもいる一方で、全然ブランコを漕げず四苦八苦する子供もいる。ブランコを漕ぐコツを覚えるのもなかなか大変そうである。考えてみれば、ブランコは一体どういう風に漕ぐものなのだろう?口で上手く説明できる人がいるだろうか?
それに、そもそも私たちはブランコを何故漕ぐことができているのだろう?
いったい、いつから疑問に思うことをやめてしまったのでしょうか? いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか?という手紙で始まるのは加納朋子の「ななつのこ」だが、「何故、リンゴは落ちるのかという謎」と同じく、「ブランコの漕ぎ方の謎」だってとても不思議だ。いつも目にする公園のブランコを、私たちは一体どうやって漕ぐことができているのだろう?
いつだって、どこでだって、謎はすぐ近くにあったのです。
何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。
もちろん、「何でブランコの漕ぎ方が不思議なのさ?」と言う人も多いだろう。その中には理路整然とブランコの漕ぎ方を説明してくれる人もいるだろう。そして、「特にブランコの漕ぎ方をじっくり考えたことなんかないもんね」という人も多いに違いない(私だけかもしれないが)。そこで、まずは「ブランコの不思議」を簡単に書いてみることにしよう。
次の図は「ブランコを漕いでる子供」である。
 |
この子供が何もせず立っているだけ(あるいは座っているだけ)だったら、どうなるだろうか?それはもちろん、単なる振り子と同じくようにブランコは動く。もしも色々な摩擦がなければ、まったく同じように動き続けるだけだし、摩擦力があればブランコの動きはただ減衰していくだけである。つまり、子供が何もしなければ、ブランコの動きは「遅く・小さく」なることはあっても、ブランコが「速く・大きく」なることはないのである。
だからブランコを速くするためには、「ブランコに乗ってる子供がブランコを漕がなければならない」わけであるが、ブランコに乗ってる子供は一体どんなことができるだろうか?
次に示す図は「ブランコに乗ってる子供を中心にとった座標軸」を描いてみたものだ。この図の中で直交する二つの軸を描いてある。つまり、
- ブランコの動きの中心を向いている軸A
- 軸Aに直交する、つまりブランコの進行方向(あるいはその逆方向)を向いている軸B
 |
ところが、実は「ブランコに乗ってる子供」はこの二つの軸の内の片方、軸Aに対しての動きしかできない。何故なら、軸B方向に対しては「ブランコに乗ってる子供」動きの支えになるモノが全然無い。だから、ツルツル滑る氷の上では全然動けないのと同じく、「ブランコに乗ってる子供」はその方向には動けないのである。もし子供がその方向に動こうとして体を動かしたりしても、結局子供の重心はその方向には全然動かないのだ。
それに対して、ブランコの動きの中心を向いている軸A方向に対してはブランコの鎖も座っている(あるいは立っている)板が支えになるわけで、その方向に対しては「ブランコに乗ってる子供」は動くことができる。
というわけで、ブランコの上では「ブランコの動きの中心を向いている軸A」方向にしか動けないわけであるが、その方向というのはブランコの進行方向に対しては直交している。つまり、ブランコを漕ぐためには、「ブランコの進行方向に対して直交している方向に動く」しかないことになる。
ここまで書くと、ブランコの不思議が判るハズだ。ブランコを漕ぐ、つまりブランコを軸B方向の速度を上げたいのに、我々は「軸Bに対して直交している方向に動く」ことしかできないのである。一体何故、軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増すのだろうか? この謎「ブランコの不思議」を、ゆっくり考えてみることにしよう。
まずは、ブランコに乗ってる子供が立ち上がったりして、「ブランコの動きの中心を向いている軸A」方向に動いた場合、何が起きるだろうか?
 |
「ブランコの動きの中心を向いている軸A」方向に動くと、ブランコの鎖の長さが短くなることと同じである。すると、回転しているブランコの鎖が短くなるわけで、そうするとブランコの速度は速くなる。何故なら、角運動量が保存されるからである。ちょうど、スケートのフィギア競技の選手が回転中に伸ばしていた手を縮めると回転数が早くなるのと同じだ。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの半分だけ(とんでもない身長の子供だ!)上がれば、ブランコの速度はもとの速度の倍になるのである!
ということは、少なくともこの瞬間は「軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増す」わけであるが、これでブランコの漕ぎ方を納得するにはまだまだ早いのである。確かに、「ブランコの動きの中心を向いている軸A方向に動く」とブランコの速度は増すわけであるが、それはその瞬間だけである。ブランコの上で「立ち上がり続ける」なんてことはできないわけで、速度が増し続けるわけではないのである。
もしも、「もう一度ブランコの上で立ち上がるために、すぐに低い姿勢に一旦戻ったり」したら大変だ。ブランコの鎖の長さが長くなるのだから、今度はブランコの速度は遅くなってしまうのである。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの二倍だけ(つまりさっき立ち上がった逆の動きである)下がれば、ブランコの速度はもとの速度の1/2になってしまうのだ!
これでは、結局さっきの速度が二倍になったことは帳消しになってしまう。つまり、「単純に」角運動量の保存を考えるだけではブランコの速度を(長い間にわたって)早くしていくことはできないわけだ。
このままでは、「ブランコを漕ぐことなんか不可能である」という結論が出てしまいそうになるが、ブランコを漕いでる子供達はイッパイいるわけで、そんな結論を受け入れるわけにはいかない。彼らがみんな超能力でブランコを漕いでいるわけもないのである。まだまだ見落としていることがあるので、ブランコの不思議の謎が解けないだけのハズなのだ。
そこで、ちょっと考えてみると「とんでもなく単純なこと」を見落としていたことに気付いた。それは、「タイミング」である。例えば、ブランコの速度がずっと同じであるすると、
- 初期のブランコの速度 = 10
- 重心位置を高くして 10 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- 重心位置を低くして 10 X 1/2 = 10 (何てこったい、速度が半分になっちまったか!)
- 初期のブランコの速度 = 10
- 重心位置を高くして 0 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- そのあとブランコの速度 = 0
- 重心位置を低くして 0 X 1/2 = 0 (0が0になっても全然変わってないもんね!ヘヘン!)
人生何事もタイミングが重要である。失恋した男性や女性にタイミングをわきまえた「恋のハイエナ」達が寄ってくるのと同じく、またお金に困っていると何故かサラ金の広告が目の前にチラチラするのと同じく、ブランコを漕ぐにはやはりタイミングが重要なのだ。
なるほど、考えがまとまってきた。このイキオイでそのまま「ブランコの理想の漕ぎ方」まで考えてしまおう。
まず、「重心位置を高くしてブランコの速度早くする」にはできるだけ速度が速い瞬間に行うのが良いだろう。倍率が確定している賭なのだから、元金はあればあるほどおトクである。1万円×2=二万円では1万円しかもうからないが、一千万円×2=二千万円では一千万ももうかるのだ。ブランコの速度が速い瞬間に立ち上がれば、一番おトクに速度を増すことができるのである。
もちろん、ブランコの速度が速い瞬間といえば、明らかにブランコが一番下にきた瞬間である。つまり、ブランコが一番下にきた瞬間に立ち上がれば「一番おトクに速度を増すことができる」わけだ。しかも、その瞬間は鉛直に重心を持ち上げることになる。つまり、位置エネルギーを効果的に増加させることができるわけだ。結局、この時に増加させた位置エネルギーは後で、運動エネルギーに変換されるわけで、結局これがブランコの運動の源となるのである。
そして、「次にもう一度立ち上がるために一旦低い姿勢に戻る瞬間」=「速度が遅くなる瞬間」はブランコが停止しているときであれば何の問題もない。ブランコはもともと止まっているんだから、その速度が何分の一になったって全然気にしないもんね!となるわけだ。そのタイミング= ブランコが止まる瞬間といえば、もちろんブランコが最高地点まで上がった瞬間である。つまり、ブランコが一番上にいった瞬間に低い姿勢に戻れば全く減速無しに次の加速に備えることができるわけである。しかも、その時には実は運動エネルギーを位置エネルギーに変えることで、隠し財産にしているわけで、もう汚い政治家のマネーロンダリングのような見事な方法なわけだ。
というわけで、
- ブランコが下に来たときに(立ってる場合は)足を伸ばして立ち上がったり、(座ってる場合は)足を曲げたりすることにより高い位置に重心を持ってきて(しかも、重力に逆らって重心を上げるため位置エネルギーが増加する)
- ブランコが上に行ったときにその姿勢を元に戻す
それでは、確認のためにそのやり方で本当にブランコが漕げるのかどうか、シミュレーション計算を行ってみた。ブランコの動きは振り子運動だが、振れ幅がとても大きいので、cosx≒xというような近似をする単振動としての扱いはできない。そこで、楕円積分の計算を行わなければならない。が、私が自分の力でできるかどうかはともかく、そこはMathematicaに解かせればイッパツである。もう、驚くくらい簡単なのである。自分の力で解いていないところが、実に悲しい現実ではあるが、それが現実なのだからしょうがない。
というわけで、ブランコの動きのシミュレーションをしてみた結果が次のグラフである。「ブランコに乗ってる子供」の漕ぎ方としては、以下の三つ
- 何もしない場合
- ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合
- ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合
 → ブランコの動きはず〜と変わらない |
ブランコが上にきたあたりで座り込んだ場合  → ブランコの動きはどんどん大きくなる 「やったぜ、これが理想の漕ぎ方だぁ。」 |
ブランコが上にきたあたりで立ち上がった場合  → ブランコの動きはどんどん小さくなる 「なんてこったい、遅くなっちまったぁ。」 |
この結果から、ちゃんと1.の「何もしない場合」は「ブランコの動きはず〜と変わらない」し、理想の漕ぎ方であるハズの2.の「ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合」は「ブランコの動きはどんどん大きくなる」し、最悪の漕ぎ方であるハズの3.の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合」には「ブランコの動きは逆にどんどん小さくなってしまう」ことがわかる。というわけで、今回考えた「ブランコの不思議= 漕ぎ方」はシミュレーション計算結果からも確かめることができたわけだ。
ところで、こういったタイミングを考えながらパラメーターを変えることで動きを大きくしたりすることは「パラメータ励振」と呼ばれる。ブランコの漕ぎ方はその「パラメータ励振」の応用のひとつである。「何故、リンゴは落ちるのかという謎」には重力という基本的な物理現象が隠されていたが、それと同じく、「ブランコの漕ぎ方の謎」にも「パラメータ励振」という物理現象が隠されているのだ。次回以降も、この「パラメータ励振」を手がかりにいくつかの「身近な謎」に迫ってみたい、と思うのである。
さて、公園でブランコを漕ぎまくる子供をもし見かけたならば、ぜひ横から子供の動きを見てやってもらいたい。きっと、その揺れ動くブランコの中にはこんな∞(無限大)の形が見えるハズだ。天まで上ろうとする「ブランコの秘密」はその「ブランコの中の∞(無限大)」に隠されていたのである。子供も含めて人間の可能性は∞(無限大)だと私は思うが、ブランコの揺れる動きから、そんなことを考えてみるのも少し面白いのではないだろうか? それとも、ちょっと考え過ぎかな。
2000-12-02[n年前へ]
■ブランコの中の∞(無限大) その1 
mail 子供がブランコをこぐということを「仕事をする」と考えます.仕事とは力に逆らって物体を移動させたりすることです.子供がブランコに乗っているとき、最下点に来た瞬間に速度は最大です.当然そのとき遠心力も最大になります.このタイミングでしゃがんでいる子供が立ち上がるということは遠心力に逆らって自分の体を移動させたと考えることができ、それは仕事をしたと考えられます. < Thank you. jun hirabayashi なるほど、判りやすい説明ですね。ただ、ちょっと気をつけなければならないのが、「 遠心力に逆らって自分の体を移動させた」という部分でしょうか。例えば、ブランコが45度の角度まで、つまり結構高く上昇した後に最下点を通過する時の遠心力を計算してみると、たかだか重力の六割弱に過ぎません。つまり、力あるいは仕事の割合から言えば、「重力に逆らって」という方が近いわけです。なので、結果的には単純に位置エネルギーを運動エネルギーに変換している、ということになるのでしょう。
2001-01-27[n年前へ]
■オッパイ星人の力学 仏の手にも煩悩編 
時速60kmの風はおっぱいと同じ感触か?
本サイトhirax.netは「実験サイト」というジャンルに分類されることが多いようである。何が実験で、何が実験でないのかは私にはよくわからないのだが、とにかく「実験サイト」と呼ばれるサイトは数多くある。そして、その数ある実験サイトの中でも、人間そして愛について日夜取り組んでいるサイトの一つが「性と愛研究所」である。その「性と愛研究所」を読んでいると興味深いことが書いてあった。テレビ番組の「めちゃめちゃイケてる!」の中で何でも「時速60キロの風圧はおっぱいの感触である」と言っていたらしい。そしてまた、「性と愛研究所」では「おっぱいの感触と風圧に関する考察」の中で、「時速60kmでは全然おっぱいの感触ではなくて、ちょうど時速100kmを境に急におっぱいの感触を感じます。」というメールを紹介しながら、
「時速100kmの風では、本物は触れないけどお手軽に疑似体験、名付けて『プリンに醤油でウニ』ではなくなってしまう。それでは、まるで『キャビアにフォアグラでトリュフの味』だ。青少年のために疑似おっぱいを探してあげる必要があるな。」と結論づけている。
この「時速60kmの風」現象は「できるかな?」的にとても興味深いと思われるので、今回じっくりと考えてみることにしてみた。そして、この結論に何らかのプラスαをしてみたいと思う。
そう、前回「オッパイ星人の力学 第四回- バスト曲線方程式 編- (2001.01.13)」でオッパイの表面で働いている力について考えてみたのは、実は単に今回・そしてさらに次回の話のための準備だったのである。(さて、ちなみに今回は会話文体をメインに話が進む。「性と愛研究所」ではないが、この手の話は会話文体の方が書きやすいように思うし、私のバイブル「物理の散歩道」でも「困ったときの会話文体」と言われていたので挑戦してみた次第である。言うまでもないが、AもBも私が書いてはいるが、私自身ではない。)
A : 「東名高速で出勤途中に確認してみたんだが、やはり時速100kmあたりが妥当な感じだったな。」
B : 「何を根拠に妥当なのかがよくわからないが、確かに時速60kmでは手に何かが触っているという感触すらないな。それにしても、哀しい出勤の景色だぞ、それ。」A : 「ほっとけ!だけど、少し考えてみると、このおっぱい(ニセモノ)の感触問題は結構面白く、技術的にもなかなかに深い話だと思うんだよ。」
B : 「はぁそうですか…、としか言いようがないな。」A : 「まぁ、聞け。何しろこのおっぱい(ニセモノ)の感触問題には流体力学のエッセンスがぎっしりと詰まっているんだからな。」
B : 「そんな話は聞いたことはないが、とりあえず聞かせてもらおうか。」A : 「このおっぱい(ニセモノ)の感触問題を解くためには、とりあえず車の窓から手を出したときの指の周りの空気流を計算すれば良いわけだ。」
B : 「ちょっと待て。何で指の周りなんだ。手のひらじゃなくて?」A : 「簡単なことさ。試しにおっぱいを揉む仕草をしてみろよ。」
B : 「こ、こうか?あぁっ?手のひらじゃなくて指で揉んでるっ!」A : 「そうだろ。何故かわからないが、おっぱいを揉む仕草=Mr.マリックが超魔術をかける時のような指使いらしいんだよ。」
B : 「うむ、確かにそのようだな。」A : 「だから、時速60kmの風からおっぱいの感触を受けているのは指先だと考えるのが自然だろ。それなら、とりあえず下の図のような「指の間を抜けていく空気の流れ」を計算してみれば、おっぱい(ニセモノ)の感触問題が解けるわけだ。」
B : 「実写の手に二次元の計算結果を三次元的に合成するという凝った処理が、実にクダラナイことに使われている例だな…」
 | 高速で走る車の窓から手を出して、その手の指の間を抜けていく空気の流れを計算しよう。 鉛直方向の指の等方性を考えて、右の図に示すような指を輪切りにするような水平面のみを考える。 こんな写真を撮るときに、自己嫌悪に陥りがちなのは何故だか知りたい今日この頃。 |
A : 「こういう「空気の流れ」ような流体の力学は、ニュートンのプリンキピアに始まり、オイラーとベルヌーイにより非圧縮・非粘性の理想流体の運動方程式とエネルギー保存則が導かれた。それがオイラーの運動方程式とベルヌーイの式だ。オイラーの運動方程式はちなみにこんな感じだ。」
加速度 = 外力 + 圧力勾配力 v : 速度 |
A : 「基本的には「加速度 = 外力 + 圧力勾配力」という形だな。この非圧縮・非粘性の理想流体の場合はラプラシアンがゼロのポテンシャル流れと呼ばれる単純な流れになる。試しに、そんな場合をNast2Dを元にしたプログラムで計算してみた結果はこんな感じになる。ホントはこの計算自体は完全な理想流体ではないのだが、まぁ大体はこんな感じだ。」
B : 「おっ、あっという間に計算したな。」A : 「まぁ、ポテンシャル流れならエクセルでもちょちょいと計算できるくらいだからな。ちなみに、これは窓から手を出してしばらくしてからの空気の流れだ。」
 |
A : 「で、どうだ?」
B : 「いや、どうだ、と言われても困るが、なんかキレイだな。だけどちょっと小さくて見にくいなぁ。」A : 「そう言われれば確かにそうだ。じゃぁ拡大してみるか。」
 |
B : 「で、この結果から何がわかるんだ?」A : 「この図で空気は左から右へ流れているわけだが、左端の空気の速度と右端の空気の速度は、実は同じなんだ。」
B : 「そう言われても、よくわからないが?」A : 「指を通り過ぎてく空気は、指をとおる前後で運動量がそのまま変わってないってことさ。つまり、空気は指を通り過ぎる時になんら抵抗を受けてないってことだ。」
B : 「えっ?おかしいじゃないか、それなら逆に言えば指も空気から何の抵抗を受けないってことか?」A : 「そういうことだ。これがダランベールのパラドックスだ。」
B : 「じゃぁ、何か?この指先に感じるまぎれもないおっぱいの感触は幻だとでもいうのか!? そんなのオレは認めないぞ!」A : 「まぎれもない、っていうほどのものでもないし、ニセモノおっぱい自体は何か一種の幻のような気もするが、もちろん感触自体は幻であるハズはない。そもそも、空気をサラサラな理想流体として取り扱ったところが間違っているわけだ。そこで、登場するのがナヴィエとストークスだ。彼らはオイラーの運動方程式に粘性を導入した。全てはおっぱいの感触を説明するために、だ。」
B : 「それウソだろ。ナヴィエとストークスが聞いたら怒るぞ。」
加速度 = 外力 + 圧力勾配力 + 粘性力 v : 速度 |
A : 「見ればすぐわかるだろうが、この非圧縮流体に対するナヴィエ・ストークスの方程式は、最後に粘性項が入っている以外はオイラーの運動方程式と全く同じだ。」
B : 「なるほど。こうしてみると意外に簡単な式だな。」A : 「あぁ、オイラーの運動方程式に粘性項が入っただけだからな。そのせいで計算はちょっと複雑になるが、最近のパソコンならノープロブレムだ。というわけで、粘性を考慮して計算してみた結果が次の図だ。」
 |
B : 「おっ、ちょっと様子が違うな。何か、ジェットエンジンみたいに尾を引いてるぞ。」A : 「そうだろ。指の後ろのl様子がずいぶんと違うだろう。で、これを拡大してみたのが次の図だ。」
 |
B : 「左端の空気の速度はもちろんさっきと同じだが、指の後ろでは空気が渦巻いているし、右端の空気の速度は全然違うな。」A : 「もっとリアルに、窓の外に手を出したときの、指の周りの空気の動きを時間を追って計算してみた計算結果のアニメーションが次の図だ。指の周りに空気が渦巻いていく様子がよくわかるハズだ。」
 | 窓の外に手を出したときの、指の周りの空気の動きを時間を追って計算してみたもの。指の周りに空気が渦巻いていく様子がよくわかる。 メッシュを細かく切ったおかげで、計算結果は1GB弱。なんてこったい。 |
B : 「指が空気の中を走り抜いていく様子がよくわかるな。確かにこれなら、空気の抵抗を受けまくりだな。」A : 「そうだ。空気は指から力を受けるし、逆に、指は空気からしっかりと力を受けるわけだ。」
B : 「なるほど、この計算結果は指先に感じるまぎれもないおっぱいの感触を説明しているわけだな。いい感じじゃないか。流体力学そして粘性項さまさまじゃないか!」A : 「あぁ、それも全てナヴィエとストークスのおかげだ。」
B : 「おやっ?ちょっと待てよ!これでは、ただ現実を説明してみただけで、何の解決にもなってないぞ!時速60kmと時速100kmの風の感触の差を説明しているわけでもないし、青少年のためのもっと安全な擬似おっぱいを提供しているわけでもない!」A : 「いや、それがそういうわけでもない。実はこの先があるんだ。このナヴィエ・ストークスの方程式の解はレイノルズ数という無次元数によって決定されるんだ。今回の場合で言うと、レイノルズ数は「指の直径x 車の速度 / 流体の運動粘性率」という形になる。そして、このレイノルズ数が大きくなるほど渦が延びていくんだ。」
B : 「なるほど、わかってきたぞ。つまりあれだな。時速60kmから時速100kmに速度を上げれば、それに応じてレイノルズ数が大きくなって、空気の渦もおおきくなるし、おっぱいの感触も確実なものになるわけだな。勉強になるな。」A : 「う〜ん、実際には密度の違いの方が大きいんだが、ナヴィエ・ストークスの方程式の理解としてはそれでいいかもな。あと、単にレイノルズ数を大きくしたかったら指を太くする、っていうのでもいいわけだ。」
B : 「そう言われても指の太さはなかなか変えられないしなぁ。」A : 「指サックとか色々手はあると思うが、もっといい方法がある。さっきの式を眺めてみれば流体の運動粘性率が小さくなれば、レイノルズ数は大きくなる。例えば、水の運動粘性率は空気のそれの十五分の一だ。」
B : 「ってことは、水の中だったら、レイノルズ数も大きいし、密度も大きいし、指先に抵抗を受けまくりってことだな。すると、水中で手を動かしてみれば、それは空気中の高速クルージングと同じってことになるな!」A : 「そうさ、風呂の中で手をひとかきすれば良いだけの話さ。何もわざわざ時速100kmの車の窓から手を出す必要はないんだ。実際、風呂の中で確かめてみたけど、なかなかイイ感じだ!」
B : 「時速100kmで走る車の窓から手を出すのに較べれば、風呂の中で手をひとかきすれば良いだけなんて、まさに青少年のためのもっと安全な擬似おっぱいだな!」A : 「あぁ、それも全てナヴィエとストークスのおかげだ。」
B : 「それはもういいっ言ってるだろ。」A : 「ところで、ふと考えてみたことがあるんだ。さっき、指を太くすれば遅い速度でもレイノルズ数が大きくなるって言っただろ。東大寺の大仏なんかかなり指が太いじゃないか。」
B : 「確かに、そうだな。」
A : 「今調べてみると、大仏の掌の長さは256cmだ。つまり普通の人間の10倍くらいある。だったら、指の太さも10倍はあるだろう。ってことは、ほんのそよ風が吹いただけでも、大仏の手にはしっかりとしたおっぱいの感触が感じられているんじゃないのかな?」
B : 「単に手が大きいから空気の抵抗も大きいだけどいう気がしないでもないが、指の長さもでかいしさぞかし超巨乳の感触かもしれんな!そう考えると、あの大仏の手も何か実にイヤラシイ手つきに見えてくるから不思議だな!」A : 「う〜ん、悟りを開いているから、指先のヘンな感触なんかには惑わされないんだとは思うけどな。しかし、案外と仏もそんな煩悩と日夜闘っていたりするのかもしれないなぁ。しかも、その煩悩がホントーにあるのかもよくわからない幻のような擬似おっぱいってところが面白くないか?大仏の指先は二十一世紀の煩悩そのものを暗示しているのかもしれん。仏の手にも煩悩ってところだな!」
B : 「言いたい放題だな、全く。」
さて、今回は「オッパイ星人の力学第四回 - バスト曲線方程式 編- (2001.01.13)」と繋がるところまで話が辿り着かなかった。おっぱいの表面張力、マボロシのような指先の流体力学、そして大仏の煩悩をめぐる大河ドラマは人生そのもののようにまだまだ続くのである。
2001-07-31[n年前へ]
■水平線の彼方 
Over The Horizon
先日、富士の五合目から地平線を眺めていたのだけれど、そこで「水平線の向こうには何があるのだろう?」なんてことをふと頭に浮かべてしまった。「そこまでしか見通せない」という線が水平線なのだから、もちろん水平線の向こうに何があるのか見えるわけがない。だけど、だからこそ「その水平線の向こう」に何があるのかが、少しばかり気になってしまった。

そういえば、少し前に英和辞書を読んでいた時に、" on [over] the horizon"で「兆しが見えて,将来起こりそうで」を意味する、なんて書いてあった。「水平線の向こう、水平線の彼方」にある「何か」は「将来起こりそうな、何かの兆し」というわけだ。
あぁ、そうかぁ、と私は思わず納得してしまった。確かに、水平線の向こうに例えばもし何かの波があれば、それはきっといつか私たちの目に見えるようになって、そして私たちの足元にまで辿り付くことだろう。水平線の向こうにある波は止まることなく進み続けているのだから、例え水平線の向こうにあっても将来必ず私たちの場所まで辿り着くのである。
もちろん、水平線の向こうにある波を私たちが見通すことはできるわけはないのだけれど、だけどその気配を私たちはきっと感じるのだろうと私は思う。「水平線の彼方」にあるものは、「将来起こりそうな何かの兆し」であって、水平線の向こうにいるその気配には強い存在感があるはずだろう。
そんな「水平線の彼方にある波」を考えるとき、私はこんな話を思い出す。
地球はよく「水の惑星」と呼ばれる。確かに、そう呼ばれるくらいに地球には水が溢れている。何しろ、地球の表面積の七割が海なのだ。しかし、そうは言っても、地球の表面が全部水に覆われている、というわけではない。私たちが生活している陸地だって、「残りの三割だけ」とはいえちゃんと存在している。それなら、表面全部が水で覆われている「水の惑星」がもしもあったとしよう。そんな水の惑星のどこかで高い津波が生じたら、一体どうなるだろう?例えば、その水の惑星の南極である日突然津波が生じたとしよう。その時その津波はどんな風に伝わっていくだろう?
その津波の動いていく様子を図示してみたのが、下のアニメーションだ。
自分と正反対の場所で生じた波が自分の足元まで辿り付いて、生まれた場所と正反対の場所で生まれた時と同じ大きな津波になっているということを考えると、どうしても不思議な感覚に襲われる。そして、自分と正反対の場所で自分の足元で生じているのと同じ高波が生じている、ということもまたちょっと不思議だ。まるで、自分と正反対の場所に「もう一人の自分」がいるみたい、だ。「もう一人の自分」が、自分からは見えない水平線の向こうにいるなんてちょっと面白い感覚だ。
南極(図の下部)で発生した津波は進むに従って、段々と小さくなっていく。最初は南極の一点に集中していたエネルギーが段々と広がって拡散していくのだから、波が進んでいくにつれその高さはどんどん低くなる。そして、赤道を通過する頃には津波の高さはとても小さくなってしまう。ところが、その波が赤道を過ぎたとたんに津波は逆に強まりはじめる。赤道を通過した後は、津波の前方はだんだんと狭まっているので、こんどは津波のエネルギーが集まり始めるわけだ。それまでは、低くなる一方だった津波の高さは、今度は逆に徐々に高くなっていく。そして、ついに津波が北極に辿り着く時には、かつて南極で津波が発生したときの高さを再現してしまう。生まれた地点のちょうど反対側で、津波が生まれたときと全く同じ高波が発生するのである。
私たちの裏側で津波が発生したとしても、その津波は徐々に小さくなりながら進み続け、そして私たちの足元でその津波は再び大きな高波となるのである。そして、その津波はその後も同じように進み続けて、また南極で大きな高波となる。南極から発した高波がもう一度南極に集まってまた高波となるとも言うことができるかもしれないし、あるいはそれは、北極で集まった高波が南極で集まってもう一度同じ高波となる、とも言えるだろう。
そしてまた、「水平線の彼方にある波」はそれと似たこんな話も思い出させる。
宇宙の曲率が正で閉じた球状空間だった場合、私たちが発した光はどうなるだろう? 私たちからどんどん離れて行く光は空間の四方に広がって行くが、何時の間にかその光は徐々に近づき始める。そして、はるか彼方のある一点でその光が集まり、そしてまたその光は広がり始める…。そしてついには、その光は私たちのいる場所に集まり始める。私たちを取り囲む全ての方向から、かつて自分が発した光がやってくることになる。かつての自分があらゆる方向に見え出すのである。
水平線の彼方には何があるのだろう?水平線の向こうを見通すことは、私たちにはできないけれど、遥か彼方にいる波は「将来必ず私たちの足元に訪れる」。そして、もしかしたらそれは「かつての自分が発した波」かもしれないし、「どこか自分と正反対の場所にいる誰かが発した波」かもしれないし、それは廻り回ってやっぱり、「自分が発した波」なのかもしないし、やっぱりそれとも…なんて考えてしまったのである。
2001-08-07[n年前へ]
■「ボケ」た背景で包み込め 
デジカメ画像をキレイにボカそう アルゴリズム編
最近、新しいデジカメを物色中である。私はこれまではFinePix4700zを使っていたのだけど、そのFinePixが半年程度で壊れてしまった。というわけで、C-4040ZOOMがどんなものか期待しているところである。
壊れたFinePixと言えば、そもそも壊れたFinePixは一台ではなかった。私はすでにFinePixを二台も買っているのだ。そして、もうすでに二台とも壊れてしまっているのである。連続殺人事件ならぬ、連続カメラ自殺事件なのである。
まず、一台目に買ったFinePix700ははメキシコのティファナでポケットから落としたら、バッテリーから電源が供給されなくなった。もちろん、ACアダプターを使えば立派に動くのだけれど、それでは少しばかり機動性に欠けてしまう。まさか発電機を持ち歩くわけにはいかないし、コンセントの近くでしか撮影することができないとなると、それは非常に困ってしまう。そこで、すかさず二代目としてFinePix4700zを私は買った。ところが、買ってから半年位たったある日、今度は勤務先の駐車場でポケットから落としてしまった。すると、今度はファインダー視野がズームに連動しなくなって、なおかつレンズがまるでジョイスティックのようにあらゆる方向に曲がるようになってしまった。
こんな風にデジカメはとっても壊れやすくて、半年毎にデジカメ出費を強いられる私に周囲は「落としたオマエが悪い」と非常に冷たいのである。残念なのだ。「そういうのは壊れたんじゃなくて、壊したんだ」と被害者である私をまるで加害者のように告発する人さえいるのである。連続カメラ自殺事件は実は他殺で、しかも犯人は私だと告発する輩さえいるのだ。ひどい話である。
ところで、C-4040に期待しているのは、コンパクトで、レンズアダプターが使えて、レンズがF1.8と明るいことなのである。コンパクトなのは持ち歩くために必要だし、私はなんと言っても超広角デジカメが欲しいのだが、そんなデジカメはないので、ワイドコンバーターを付けたいのでレンズアダプターが必要なのである。明るいレンズの方は、うす暗い中でも撮影する時に重宝しそうなので、少し期待しているのである。
ところで、この位明るいレンズであれば、もう少しぼかすことができるものだろうか?デジカメで写真を撮ってもどうしてもボケない。35mmフィルムを使っているカメラなどと比べるともう全然ボケない。もうほんとにボケない。
例えば、35mmカメラで135mm F4.5開放のレンズなら、ピントの合ってない背景はこの位はボケる。これは京都の哲学の道近くにある吉田山で撮った写真だ。
 |  |
ピントが合っている位置以外は光がボケて、キレイなボケが発生する。どちらの写真も絞りは開放で撮影しているので、後ろの風景はほぼ丸くボケている。ぼかせばキレイというわけではないけれど、背景などがごちゃごちゃしている中で対象物だけを浮き上がらせたい場合には、「ボケ」させるととても良い感じになる。
しかし、デジカメではそうそう簡単にボケた画像を撮影することはできない。35mmフィルムに比べて、CCDサイズが小さいからである。35mmカメラよりAPSカメラはもっとぼけなくて、それよりデジカメはさらにボケないのである。そんな様子を見るために、二台目として買ったFinePix4700zで「ボケ」を意識して撮影してみたものが下の写真である。手前の植物にピントが合って、奥の道の先はボケてはいるのだけれど、それでも先程の写真などとは比べものにならないほどわずかしかボケていない。
 |
ところで、このような画像の「ボケ」を考えるとき、「ボケ」た画像をシャープに復元しようという話は非常にポピュラーな話題である。例えば、本「できるかな?」でもこれまでに
といった感じで遊んできた。また、さらには「恋の形」を復元しようとしたとか、このようなアプローチを遥か昔に考えていた漱石の「文学論」を振り返ってみたりしたきたのである。しかし、これらはいずれも「ボケたデータを復元する」という問題であった。一方、この逆のアプローチである「シャープなデータをボケたデータにする」という問題も結構ポピュラーである。例えば、音楽をホールやライブハウス風にボケた音にするDSPはかなりの数のオーディオ装置に付けられている。これも、もともとはシャープな音声データが部屋の中でボケていく様子をシミュレートする回路である。また、画像に関する話題でも、ピント位置をずらした複数の画像から任意の「ボケ」画像を作成するといった話題もたまに見かける。
そこで、「できるかな?」でもデジカメ画像を35mmカメラ風にキレイにぼかすことに挑戦してみることにした。今回は、まずはアルゴリズムを確認して、次回以降で簡単プログラムを作成してみることにしたい。
まずは、似たようなソフトウェアがあるかどうか、Googleで適当なキーワードを使って検索をかけてみると、IrisFilter(http://www.reiji.net/iris/)というソフトウェアがあった。これは、「写真のぴんぼけを再現する」というフィルターだった。サンプル写真などを見てみると、これがなかなかきれいだった。例えば、早朝の御殿場の路上を「在りし日のFinePix4700z」で撮影した写真にこのフィルタをかけて、「ボケ」を加えてみたのが下の画像である。
 |  |
ここではこんな![]() 六角形の絞り形状をを用いてみた。右の処理画像中の、車のテールランプや車の下部を眺めてみると、鋭いハイライト部が六角形に光っているのがわかだろう。確かに、「ボケ」がカメラの絞り形状になっていて、良い感じである。
六角形の絞り形状をを用いてみた。右の処理画像中の、車のテールランプや車の下部を眺めてみると、鋭いハイライト部が六角形に光っているのがわかだろう。確かに、「ボケ」がカメラの絞り形状になっていて、良い感じである。
WEBページの記載によれば、このIris Filterは「フィルム特性曲線を利用し、レンズから通った光がフィルムを感光させる様子を再現しています」ということである。なんでも、特許も国内・USP共に出願済みということだが、特願2000-100042もU.S.PTO 09/772532も未だ公開にはなっていないようで、残念ながら特許の内容を読むことはできなない。
このWEBページの記述の中で面白いのは、「データ上の数値をそのまま拡散させる従来のPhotoshopをはじめとした画像処理ソフトと違い、実際のフィルムに当たる光の量(露光量)を逆算し、その露光量をもってピントがずれている様子を再現します」という歌い文句でPhotoshopの「ガウスぼかし」と比較広告してある部分である。
試しに、先の画像をIris Filterで「ボケ」を加えた画像と、Photoshopの「ガウスぼかし」とで「ボケ」を加えた画像を比較してみると、下の二枚の画像のようになる。確かにIrisFilterの売り文句通り、こうして比較してみるとPhotoshopガウスぼかしが写真の「ボケ」っぽくないのに対して、IrisFilterの「ボケ」が写真のそれっぽいことが良くわかる。
 |  |
さて、お仕着せのソフトを使ってみるだけではなくて、自分でデジカメ画像をキレイに「ボケ」させてみることにしたい。というわけで、hirax.net風「ボケ」フィルターの動作を考えてみる。
まずは、毎度のことだがオリジナル画像が「ボケ」る様子を計算する式は
逆フーリエ変換( フーリエ変換( オリジナル画像 ) x フーリエ変換(ボケ具合 ) )と表すことができる。詳しくは、「宇宙人はどこにいる?」の回でも読んでもらうことにして、簡単に言えば周波数領域でオリジナル画像とボケ具合を掛け算をしさえすれば良いのである。つまり、今回のデジカメ画像をぼかす場合だったら、
- デジカメ画像と「ボケ」具合をそれぞれフーリエ変換し周波数空間に変換
- 周波数空間で乗算を行う
- 逆フーリエ変換して実空間に戻す
じゃぁ、早速やってみようとなるわけだが、その前にもう一つ注意することがある。それは、RGB画像の数値というものは実は元々「明るさを対数変換した値」であるということなのである。人間の目も含めて世の中の大抵の材料は対数的な感度を持っている。例えば、人間の目に「2倍明るい」という場合に、光は「2倍明るい」というわけではない。その場合には指数的にX^2倍明るいのである(ここで、xの値はそれぞれのデバイスによって色々と違う)。その明るさをRGB画像の数値データにする時に、明るさの対数をとってLog[x,X^2]で2という数値として表しているわけだ。
RGB画像の数値が「明るさを対数変換した値」だというようすの一例を示すと下の図のようになる。
横軸 = 0〜255の数値データ 縦軸 = エネルギー  | 横軸 = 0〜255の数値データ 縦軸 = エネルギー  |
逆に明るさからRGB画像の数値データへの変換グラフは例えばこんな感じである。RGB数値で200と255と言っても実はその明るさは大違いであることがわかると思う。
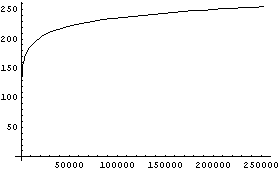 |
だから、この手の処理を行う際には、まずは指数変換してから処理を行い、そしてその後対数変換してやらなければならないわけだ。もちろん、今回のデジカメ画像をぼかす場合にも、RGB画像の数値をまずは指数変換した後、「ボケ」演算を行って、その演算結果を対数変換でRGB画像の数値に戻してやらなければならないのである。といっても、別に難しい話ではなくて画像を扱う装置だとごく当り前の話だ。
そう、「ボケ」演算のhirax.net風レシピはたったこれだけ〜というわけで、早速このレシピに従ってhirax.net風デジカメ「ボケ」フィルターをかけてみたのが下の画像である。キレイな「ボケ」画像ができあがっていることが判ると思う。
 |
ところで、デジカメ画像のRGB画像の数値を指数変換したものに「ボケ」演算を行ったわけだけれど、もしRGB画像の数値そのものに対して「ボケ」演算を行ったら、どんな結果になるだろうか?つまり、「データ上の数値をそのまま拡散させる」やり方をしたら、どうなるのだろうか?そこで、試しにRGB画像の数値そのものに対して「ボケ」演算を行ってみるとこんな結果になる。
 |
何だかボンヤリとにじんだだけの「キレイじゃない」写真になってしまっている。それは、当り前である。本来2倍明るいものはX^2倍明るいわけで、すごく光の量は2倍どころでなく多いわけだ。それが広がる量を仮にRGB数値そのまま2倍として扱ってしまうと、その光の部分は薄暗くなってしまう。コントラストのはっきりしない、ぼんやりとした写真になってしまうわけだ。ちゃんと、X^2倍のデータとして扱ってやらなければならないわけである。
試しに、指数処理したものと線形処理をしたものとを並べてみるとその画像の違いがよくわかるだろう。
キレイなボケ画像(指数処理)  | キレイじゃないボケ画像(線形処理)  |
さて、今回はデジカメ画像の「ボケ」フィルターのhirax.net風レシピを確認してみた。次回(と言ってもいつになるか…)以降に、このレシピに従って実際にソフトを作成していこうと思う。
ところで、「文学論」の中で漱石は「ボケ」は焦点的印象又は観念に付随する情緒を意味する、と言っている。それは、言い換えれば「何かの出来事をきっかけとして感じた怒り・悲しみ・喜びなどの感情がボケである」ということだ。そして、さらに言えば、写真で背景をぼかすということは、つまり「背景にある出来事が生みだした怒り・悲しみ・喜びを広く混ぜて包み込む」ということなのである。
だから、何かを撮影する時に対象物の背景をぼかすということは、「背景にある出来事が生みだした怒り・悲しみ・喜びを広く混ぜて対象物を包み込んで、そして対象物を浮き上がらせる」ということなのかなぁ、とぼんやりと考えてみたりする。そんな写真は対象物を写しこんでいるのと同時に、それを包みこむ背景も写しこんでいるンだろうなぁ、と考えてみたりする。