2001-01-13[n年前へ]
■オッパイ星人の力学 第四回 
バスト曲線方程式 編
先日、父から封書が届いた。二十一世紀にもなったというのに、e-mailでもなくて封書が届いたのである。これは、やはりアレだろうか。いい年にもなってるのに、クダラナイWEBサイトを立てているデキの悪い息子を厳しく叱るためだろうか？しかも、そのクダラナイWEBサイト(しかも、有害公式認定サイト)の名前が自分の名前(hirax)だったりするからだろうか？それとも、「本が出たなら送れ」とは言われても実は送りたくなかった「あの本」を、少し前に父に送ってしまったからだろうか？いや、それとも…そんなこんなでドキドキしながら封筒を開けると、記事のコピーが二つ入っていた。他には何も入っていないのである。一体これは何の記事だろう？と思いながらそのコピーを眺めてみた。すると、まずひとつは去年の12月25日付けの毎日新聞の科学欄である。二十一世紀を専門家達が予想した記事の横に「究める」というコーナーがあって、そこに「女性の胸と男性の好みの進化的関係は？」というインタビュー記事があった。そして、その記事が蛍光ペンでマーキングしてあったのである。
これは一体、どういうことなのだ？と頭の中がグルグル＆複雑な気持ちになりながら、とりあえずその記事を読んでみた。すると、この記事がとても面白い。インタビュー中の
ヒトは異性をどう選ぶのか？そんな疑問から女性のバストと弾性の好みに進化的関係があるかを研究している。という東大大学院の東海林さんの語りもとても面白いし、バストサイズを5段階に変えた女性の合成写真を使い、男子学生300人にアンケートしたという実験とか、巨乳好きの性格が父から受け継いだものであるかを調べるために、父子間で性的好みが伝達されるかを調べる、などの話もとても面白い。最高である。(中略)小さいバストほど魅力的だと母に教えられて育った。しかし、大きいバストが好きな男性がいることに気付いて驚き、「なぜ」と考えたのが研究のきっかけだった。(中略)「大きいバストが本当に普遍的に好まれるかを知りたい。控えめなバストが淘汰されてしまうとは考えたくないから」と話す。
そして、父からの封筒に入っていたもう一つの記事は宇宙科学研究所の新聞の中の宇宙基地利用研究センターの黒谷氏の「Anti-Gravity」というエッセイだった。なんでも、Anti-Gravityという化粧品があって、
それは顔の皮膚のコラーゲンに皮膚がたるまないようにするというものらしい。顔の皮膚にハリをあたえて、顔のたるみを防ぐのである。顔の皮膚のたるみ元をたどれば重力のせいだから、「anti-gravity= 無重力」化粧品ということになるわけだ。じゃぁ、このAnti-Gravityを体中に塗れば、バストやヒップが垂れるという女性の悩みもなくなるのではないか、と「無重力における生物の専門家」である黒谷氏は書いていて、参考文献に本サイトが挙げられていたのである。
うむむ、世の中には巨乳の科学について進化論的に研究している人がいたり、オッパイの力学について考え（てみたりもす）る無重力生活の専門家もいるのだ。これはマズイ。油断している場合ではない。私もオッパイ星人研究をもっと真剣にしなければならない。父はきっと私に「研究の厳しさ」を教えようとしたに違いないのである。私の父はこれまでの「オッパイ星人の力学」を読んで、美味しんぼの海原雄山風に「うわあっはっ、こんなものでオッパイ星人の力学だとは笑止千万！」位のことを言ったに違いないのである。
しかし、それだけではない。「二十一世紀、小さいバスト、大きいバスト、無重力、皮膚、オッパイのたれ」というヒントを与えてくれたのである。ここまでされて何かを書かなくて何としよう。オッパイ星人研究の手は一瞬たりとも休めてはならぬのである。そこで今回は「皮膚のハリ」や「重力」を気にしながら、「オッパイのたるみ・形状」について考えてみることにした。
さて、一体バストの形状というものはどうなっているのだろう？これまでの「オッパイ星人の力学」では
- 半球モデル
- 円錐モデル
そしてもちろん、このモデルに対して不満を持つのは私だけではなくて「これらのモデルには私は納得できません。」というメールがたくさん送られてきた。それどころか、「本当のオッパイをあなたは知らないのではないですか？」という実に失礼？なメールさえ送られて来ていたのである。「それでは、参考までに本当のオッパイの資料でも送って頂けないでしょうか？」とは私は大人なので返事をしなかったが、ちゃんとしたモデルを作らないことにはこれからもそんなメールがまだまだ来るに違いないのだ。
というわけで、今回は新しいバストの形状モデルを提唱してみたい。それは「バストの内部は液体に満ちていて、その液体を外側の皮膚が支える」という
- 水風船バストモデル
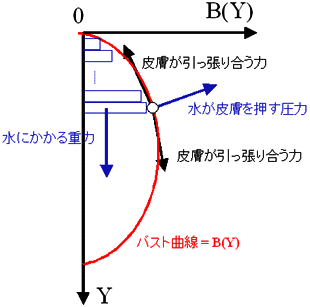
こんなモデルに基づいて、バストの形状を計算するにはどのように考えれば良いだろうか？次の図が「水風船バストモデル」における内部の水と各皮膚部分にかかる力を示してみたものである。これはバストの断面をを鉛直方向に示しており、左の黒い鉛直線が胸板であり、赤い線がバストの形状を示すバスト曲線である。（ちなみに、今回はバストを二次元の断面でのみ考えている。）
赤い線がバストの形状を示すバスト曲線
|
「水風船バストモデル」における内部の水には重力がかかり、バストの下の方にいくほど圧力がかかっている。そして、皮膚に面している内部の水はその圧力を皮膚に伝える。そして、皮膚はその圧力で変形しながら水で満ちたバストを支えるのである。この時、バストの形状= 皮膚の形状を示すバスト曲線はどんな条件を満たしているだろうか？
ここで、胸板にそって下向きにY軸をとり、バスト曲線をB(Y)で表すことにしよう。上の図をよく眺めるとわかると思うのだが、バストの形状= 皮膚の形状を示すバスト曲線をB(y)とすると、バスト曲線B(y)は実はこんな方程式を満たす。
 |
まぁ、ここでは簡単のために、係数を省略していたり、バストが本当に垂れてしまうような状況は考えていなかったりするので、ごく簡易的なバスト曲線方程式だと思って欲しい。大雑把に係数などを無視して、言葉で言ってしまえば、バスト曲線の傾きの変化はその点より上に位置するバストの重量に等しい、という感じである。自由境界におけるLaplaceの関係でも連想して頂ければわかりやすいだろうか？とにかく、この条件と適当な境界条件さえ入れてやれば、「水風船バストモデル」におけるバスト曲線B(y)は計算することができるのである。
さて、このバスト曲線方程式を一般化したり、係数をちゃんと計算したり、三次元に拡張したりということはまたいつか行うことにして、まずは適当にこのバスト曲線方程式を数値的に解いてみた。それが、例えば、次の図である。これが、「水風船バストモデル」のバストの形状の一例だ。
赤：すごくハリのあるヤングな皮膚の場合
|
この図の中でバスト形状のプロットが三種類あるのは「皮膚のハリ = 皮膚のヤング率」として三種類の値を使ってみたからだ。以前
の中でそう、もうお判りのはずだ。 「バストに関するヤング率」はまさにヤング率(Young率)なのである。実は年齢に比例する係数だったのだと書いたが、あれと同じである。今回は、年齢で変わっていくバストの皮膚のハリを「バストの皮膚のヤング率」とおいてみたのである。そういうわけで、皮膚のハリ= 皮膚のヤング率によってバストの形状は異なるわけだが、まずは眺めてみてもらいたい。以前のどうみても不自然な「半球バストモデル」等に較べて、ずっとましになっているとは思わないだろうか？特に、藍色・マゼンダのプロットなどかなり自然な形状になっていると思うのである。感受性の豊かなオッパイ星人であれば、必ずしやググッとくるハズである。
さすがに、メチャクチャ皮膚のハリがある赤色のプロットなどは松坂大輔もビックリの「超ロケット乳」になってしまっているが（といっても、この図のアスペクト比に意味はないんだけど）、今や時代は二十一世紀、宇宙へロケットで飛び出す時代だと思えば、こんな「超ロケット乳」を眺めるのもそれまた一興ではないだろうか。ぜひこの「超ロケット乳」には宇宙へ飛び出してもらいたいものである。
もちろん、世の中には「大きいことは良いことだ」という巨乳大好きオッパイ星人達もいるわけで、そんな人達のためにもう少し「大きいバスト」の場合で計算してみたものと並べて比較してみたのが次の図である。
|  |
個人の好みもあると思うが、けっこう自然な「巨乳形状」が再現できている。ちなみに、今回使用した簡易的なバスト曲線方程式ではすごく巨乳だったり、皮膚のハリが無さ過ぎてあまりにバストが垂れている場合の計算はできない。簡単に言えば、Yに対してバスト曲線B(Y)が一対一対応しないためである。が、それゆえに巨乳と言っても美乳の範囲のみ考えることができるのである。
また、この「小さいバスト」の場合と「大きいバスト」の場合の比較から、「巨乳は垂れるのよっ！だから、小さい方が良いのっ！」という世の小振りなバストの女性がよく言うセリフの妥当性も確認してみたいところではなるが、そういうことは何か危険なことであるような気もしてきたので、今回は止めておきたい。
ところで、今回の話はAnti-Gravityから話が始まっているわけだが、ちなみに「水風船バストモデル」は無重力下ではどのような形状をとるかと言えば、当然体積に対して表面積が最小となる「半球形状」になる。つまり、「半球バストモデル」は「水風船バストモデル」の重力を無視した特殊な場合であり、逆に言えば「水風船バストモデル」は「半球バストモデル」にバスト内部での重力の影響を加えて一般化したものだったのである。
今回は、とりあえず新たに「水風船バストモデル」を提唱し、そのモデルにおけるバスト曲線B(y)を解くための簡易的な方程式を考察し、それを数値的に試しに解いてみた。次回は今回行った考察を用いながら、少し違うアプローチで「オッパイ星人の力学」を考えてみたいと思う。
さて、今回の話のきっかけともなった黒谷氏らの書いた本「星と生き物たちの宇宙」は原稿のごく初期の段階で実は読ませてもらっていた。その時感想を聞かれたときは、この本はメールのやりとりで構成されているので、「なるべく著者達の私的な部分を消さないままにしておいた方が面白いんじゃないか」なんて適当なことを言っていたのだった。その著者達が書いたこの本のあとがきの言葉を最後に引用して、これからの「オッパイ星人の科学」への「戒め」と「言い訳」としておきたい、と思うのだった…
科学は応用を通じて実生活に関わり、知的追求というこころの喜びにも関わる二面を持っています...多くの人に、こころを喜ばせる科学を楽しんでもらいたいですね。 H.Hirax, A.Kurotani
2001-07-01[n年前へ]
■小さな掌に未来の地球儀をのせて
この手で地球を作ってやろう
先日、「サラリーマンとして会社に入ったからには社長を目指すのが当り前」と言う人とじっくりと話をしていた。まぁ、その話の内容はそれはそれで結構面白かったのだけれど、何故かその時私は映画の１シーンを思い出してしまった。チャップリンの映画「独裁者」の中で、世界制覇を目指すヒンケルが地球を模った風船を抱きしめようとして、結局その風船を割ってしまうあのシーンである。
私と話す相手の背中のずっと向こうにその地球の風船を眺めながら、私はそれとはちょっと違う地球儀をさらに思い浮かべていた。それはこんな正二十面体の小さな地球儀である。正二十面体の表面に地球の表面の写真を描いたものだ。
 |
大学の教養の頃だったか、それとも大学院に入ってからだったか覚えていないのだけれど、こんな「正二十面体の地球儀」を先生の一人がよくポケットから出して使っていた。それは、もしかしたら今考えてみればFullerが作ったDymaxionMapに影響されたものかもしれないし、その先生が独自に作ってみたものかもしれない。その辺りのことも聞いたことがあるような記憶もあるのだけれど、聞いた内容はもうとっくの昔に忘れてしまった。ただ、ポケットから小さな地球儀を手品のように取り出す仕草がとてもかっこよく見えたことは覚えている。
小さな、だけど立派に地球儀の役を果たす正二十面体をサッとポケットから取り出す仕草は、まるでのび太のために秘密道具をポケットから取り出す「ドラえもん」のようだった。もしかしたら、私に「独裁者」のヒンケルより大それた「ドラえもんになりたい」という野望を持たせるに至った理由の一つは、その小さな正二十面体の地球儀にもあったのかもしれない。
その先生が自分で作って持っていたのは、たった一種類の地球儀だけだった。だけど、そんな正二十面体の表面に色んな写真や地図、例えばそれは衛星写真であったり、国別に塗り分けられた世界地図であったり、あるいは月の表面の写真であったり、を貼り付けて色々な地球儀や月儀を作ってみたい、とその頃からずっと思っていた。そこで、そんなことができそうな道具を探してみると、
- PaperaArto(ペーパークラフトのページ）
- ( http://hp.vector.co.jp/authors/VA023341/arto/hp_arto.htm )
しかし、少しばかり考えてみれば「道具をサッとポケットから取り出すドラえもんになりたい」と野望を持つくせに、道具を探すばかりではあまりに恥ずかしい態度ではないだろうか。ドラえもんが人の道具に頼ってばかりでどうする？というわけで、急遽そんなことができるソフトを作ってみた。それがこのIcosahedronである。というわけで、いつものごとく「必要は発明の母」で「父は私」なのである。
とりあえず、このIcosahedron.exeを使うと、Windows Bitmapファイルとして保存されたメルカトル図法の地図を、正二十面体の展開図に変換した後に、Bitmap画像に保存することができる。
Icosahedron.exeの使用手順は次のようになっている。いつものように「動いてしまえば、ハイそれまでよ」というプログラミング態度なので、ボタンを押す順番が違うと動作しなかったりするけれど、その時は単に動かないだけで、大した問題はないと思う（多分）。- Loadボタン → メルカトル図法で描かれた地図ファイルを読み込む
- Resizeボタン → 作成する正二十面体のサイズを決める。プリンタでの出力解像度、正二十面体の直径（とは言わないかな）を決める。
- Convertボタン → 正二十面体の展開図を作成する
- Saveボタン → Windows Bitmapファイルとして正二十面体の展開図を保存する
 |
画面の上半分に読み込んだメルカトル図法の地図が表示され、画面の下半分には作成した正二十面体の展開図が表示される。もっとも、正二十面体の展開図の「のりしろ部分」は一部表示をはしょっているので、下の訂正図を参考にして切り取って欲しい。
 |
上の図のような正二十面体の展開図をプリンターで出力して、さらにそれを切り取って、正二十面体の地球儀を組み立ててみたものが下の図である。
 |  |
ところで、私がかつて在籍していた研究室は「理学研究科 地球惑星科学専攻地球物理学分野 測地学講座」という名前なのである。その名前を見れば一目瞭然、私はまさに「地球を描くための英才教育」を受けてきた？のである。「その実力を見せてやれ」というわけで書いてみたのが下の図だ。これが「私の世界地図」である。
 |
確か地球ってこんな感じ？というわけで書いてみたのだが、どうもおかしい。いや、はっきり言えばかなりヘンである。アメリカ大陸の辺りなんかむちゃくちゃ無理がある。コロンブスが使っていた大航海時代の（アメリカなんかなかった頃の）地図の方がよっぽど正確に違いないのである。そう私には地球を描く実力なんかはなから無いのであった。そう、哀しいけれどこれっぽちも無いのである。
いや、そんなことはどうでもいいのだ。とりあえず、私の世界地図を使って「私だけの地球儀」を組み立ててみたのが下の写真である。
 |
まるでSF映画の異世界の星みたいな感じになってしまったが、誰が何と言おうとこれが「私だけの地球儀」なのだ。世界にたった一つの私だけの地球儀なのである。
もちろん、私には私だけの地球儀があるが、それは誰しも同じハズである。十人十色、十人の人がいれば十個の地球儀があるはずだ。だから、こんな「私の地球儀」だけではなくて、これを読んだ方はぜひぜひ色んな地図を書いたり、手に入れたりして、色んな地球儀（それとも月儀、メルヘンちっくな人だったら例えば「星の王子さま」の「星儀」なんてのもいい感じかも…etc.）を作成してみてもらいたいなと思う。
そして、特に世界地図を覚えているわけもない小さな子供達に世界地図を書かかせてみて、そしてこんな正二十面体の地球儀を組み立ててみたらきっと面白いことだろう、と思う。「独裁者」の中のヒンケルみたいに地球の風船を抱きしめて遊ぶなんて、とてもイヤな感じだ。けれど、小さな子供達がそれぞれの世界地図を描いて、その世界地図で正二十面体の地球儀を作って、そしてそれぞれの小さな掌にその正二十面体の地球儀をのせて遊ぶ、なんてのはとても素晴らしく良い感じだと思う。
子供達がどんな世界地図を描くかは想像もできない。きっとずいぶんとヘンテコな世界地図がイッパイ出来上がるに違いない。そして、そんな世界地図から生まれる地球儀だって、奇妙奇天烈なものになること間違いなしだ。
だけど、その地球儀はもしかしたら未来の地球儀かもしれない。だって、子供達が未来の地球を作るということも、それもまた事実なんだから。子供達が小さな掌に未来の地球を乗せて作っていくのだから、この正二十面体の地球儀は本当に「未来の地球儀」に違いないと思うのだ。
2002-06-03[n年前へ]
■カードサイズの「画像探偵セット」!?
お手軽線数メーターを作るのだ
「どんなものでも、自分の目で眺めてみた〜い」と、ワタシはいつでも思う。世の中スベテのものを、自分の目で眺めてみた〜いと思う。しょんべん小僧が空中に描き出す放物線、巨乳ギャルにロックオンするオッパイ星人の目の動き、ビデオにかかるモザイクの向こう、はたまた田代まさしが恋い焦がれるミニスカートの結界の秘密、とにかく世の中のものスベテを何でもかんでも眺めてみたい、覗いてみたい、とワタシはいつも思っているのである。（とはいえ、誤解されると困るので念のために書いておくが、もちろんミニスカートの中を覗いたりはしないのだ）
そんなわけで、ワタシのケータイのストラップには「ちっちゃなちっちゃな虫メガネ」がついている。この虫メガネを武器にして、ワタシは色んなモノを覗くのがクセになっている。スーツ姿で出張している時だって、おもむろにこの虫眼鏡を取り出して、色んなものを覗いてみたりしているのである。
 |
だから、毎朝届けられる新聞に折り込まれているチラシやカタログを眺めるときだって、そんなカタログに「ちっちゃなちっちゃな虫メガネ」を向けてみて、その「虫メガネ」を通して、カタログがどんな風に印刷されているかをよく眺めてみる。下の左のようなカラーの綺麗なカタログだって、「虫メガネ」を通して眺めてみると、右の拡大写真みたいに、四色（シアン、マゼンダ、イエロー、ブラック）が規則正しく並んでいるようすが見えてくるのである。離れてみればキレイな写真が「虫メガネ」を通して眺めてみるだけで、こんな風に様子が変わるなんてとても不思議な気分になったりするのである。まるで、女性の化粧のように不思議で、こんな四色の手品はとても面白いのである。
| （左上と右上部分はマゼンダとシアンだけを見やすくしてみた）
|
で、こんなカタログの拡大図を眺めていると、四色に分けられた色がどんな風に並べられ形作られているかを、知りたくてたまらなくなったりする。つまり、「どんな間隔でこの色は配置されているのだろう？」とか「一体、どんな角度でこの色は並べられているのだろう？」とか思うわけである。もちろん、この画像に二次元フーリエ変換などをかけさえすれば（周波数解析をすれば）、「どんな角度で・どんな間隔で色が並べられているか」ということは知ることができるけれど、まさかワタシの頭の中でそんな作業ができるわけはない。かといって、このカタログを読み込むための「画像読みとり装置」や「解析をするためのコンピューター」を毎日持ち歩くなんてこともできるわけもない。
そこで、「どんな間隔でこの色は配置されているのだろう？」とか「一体、どんな角度でこの色は並べられているのだろう？」とかいう疑問の答えがすぐ判るように、先日こんなカード、ぴったりクレジットカードサイズの透明シートに規則的なパターンを印刷したカード、を作ってみた。名付けて、Peco-Chartなのである。
これはもちろん、判る人には判るだろうが、ハンディ「線数メーター」というモノである。一言で言えば、画像の周波数解析をとっても簡単にすることができる手品の小道具のようなカードなのだ。
 |
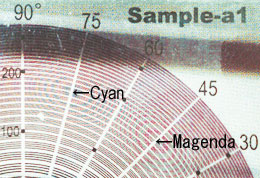
例えば、さっきのカタログの上にこのPeco-Chartを重ねて置いてみると、アラ不思議、何やらヘンな模様、不思議なモアレ模様が浮かび上がってくる。下の左の写真、あるいは右の拡大写真を眺めてみればマゼンダとシアンの同心円がハッキリと浮かび上がっているのが見えるだろう。例えば、シアン色の場合は75°の角度で175線（175線/inch）位の位置、そしてマゼンダ色の場合は45°の角度で同じく175線位の位置を中心として、同心円状のモアレ模様が浮かび上がっている。
つまり、「このカタログはシアンは75°の角度方向に1インチ辺り175個のドットが並べられていて、マゼンダのドットは45°の角度方向に並べられている」、ということを、このPeco-Chartを重ねて置いてみさえすればたちどころに知ることができるのである。
 |  |
 |
こんなペラペラのカードで周波数解析ができるなんてとても不思議に思えたりもするけれど、ちょっと考えてみればこれはごく当たり前の話である。
でも似たようなことをしたように、モアレというものは「二種類以上の何らかの模様（パターン）が干渉して発生する」ものである。つまり、ある意味「二つのパターンの相関をとる」ということである。そしてまた、少し考えてみれば「画像の周波数解析」というものは「対象となる画像」と「基準関数（三角関数etc.）」の間で相関を調べることと同じである。だから、「基準となるパターン」を「対象となる画像」の上に重ねてみた時に見えるモアレのパターンは「対象となる画像」の周波数解析結果を実は示していると考えてみても良いのである。だから、このPeco-Chartはクレジットカードサイズのペラペラなちっぽけなヤツではあるのだけれど、実は色んな画像の周波数解析をしてくれるスゴイヤツだったのである。そして、こんなポケットに入るほど小さい線数メーターははなかなか無いので、、カード入れからコイツを華麗に取り出してみせたりすると、うらやましがる人もとても多く（仕事柄、画像出力に関わる人達が多いから）、なかなかに気持ちが良いのである。 とはいえ、自慢してばかりでは何なので、さらに大量に配布すべく新たなPeco-Chart二号機をデザインしてみた。それが、下の名付けてPecochartproである。
 |
このPecochartproの謳い文句はその名の通り「プロ仕様」というわけで、画像出力に関わっている何人ものベータテスター達（自分も含めて）の感想をもとにして、
- 70線から350線までの線数とスクリーン角度の測定ができる「線数・角度メーター」（分解能を2線単位から1線単位へと二倍向上、スクリーン角度のガイドは2.5度刻み）
- 90線から410線までの線数を高精度（0.25線刻み）に計測することができる「線数メーター」（新機能）
- 線・文字の太さを計測できる「線幅スケール」（新機能）
- 〜30級、〜30ポイントまでの文字サイズ（級数、ポイント）測定ができる「文字スケール」（Peco-Chartと同じ）
- 「8cm定規」（Peco-Chartと同じものを使い勝手はそのままにコンパクト化）
- そして、便利な「画像に関する換算表」（内容を従来比75%増量）
それにしても、何か自分に役に立つツールを作るというのは本当に楽しい作業だった。手作りツールぎゃらりい脇色彩研究所ではないけれど、こんな「hirax.netオリジナルグッズ」をいっぱい作って「探偵セット」ならぬ「できるかな?セット」として、面白メールをくれた方にプレゼントとかしてみたら楽しいんだろうなぁ、と思うのである。というわけで、そんなツールをせっせと作るのだぁ、なんてことを実は計画中なのでした、ハイ。
2002-12-12[n年前へ]
■黒谷"和泉" 明美さん＠ネットサイエンス・インタビュー・メール
今朝届いてたネットサイエンス・インタビュー・メールを夜になってから眺める、と何処かで見たようなお名前。いや、見たような所ではなくて、hirax.netにアカウントがある黒谷"和泉" 明美さん＠宇宙科学研究所、である。 というわけで、そのメール中に書かれていた『絵でわかる細胞の世界』のネット上での原画展のURLを見てビックリするのだった。
2003-03-06[n年前へ]
■伊能忠敬は何処を歩く？
「音楽の“サビ”だけ抜き出す試聴システム」の「もともとモーツァルトの頭のなかで楽曲すべてが2次元的に見えていたのだとしたら、既存の楽曲であっても、それを2次元的に解析して見ることができれば、モーツァルトのように、『天才』にしか見えなかった世界を見ることができるようになるのかもしれない。」という「構造解析という音楽の地図」と題する文章を読みながら、それを読む数分前に書いた、そして読んだ「別の世界の地図」「別の世界の測地学」に関するメールを思い浮かべた。
そのメールを書きながら「そういえば、私は測地学研究室の卒業生だったんだなぁ」と思い出していた。同じようなことをしていたんだなぁ、と不思議な既視感におそわれた。
一体、21世紀の伊能忠敬はどんな世界を歩いて、どんな地図を作るのだろう？
」など。