1999-11-13[n年前へ]
■やっぱり、ウニが好き ! 
Dr.フラーはウニの夢を見るか?
私は野球は特に好きでも嫌いでもないが、野球場でビールを飲むのは大好きだ。と、始めると
の間違いと思われるかもしれない。しかし、それは違う。今回は、ウニとドームハウスの共通点について、考えてみたい。ただ、かなりビールが脳みそにしみているせいか、少しドンデモ話になるかもしれない。そこは、「ビックエッグの力学」と共通である。 私の中では、野球観戦と言えば、ビールだ。野球にはビールが良く似合う。そして、今現在も目の前にはビールがある。そして、寿司がある。といっても、スーパーで買った安物である。二つ合わせても1000円にしかならない。
 |  |
安物といっても、私の住んでいるのが港町だから安い、ということもある。何しろ、ほとんどのスーパーの魚売り場でイルカの肉なども置いてあるのだ。嘘ではない。ホントにホントである。私も、引っ越してきた当時はビックリしたが、本当である。アメリカの動物愛護団体が見たらびっくりの風景だろう。「イルカと人間はお友達」と言ってる人には見せられない風景だ。
あまりおいしそうではないので、私はまだ実際に味わってはいない。しかし、地元の人の中には「よく食べる」と言う人もいる。いつか、挑戦してみたい。
さて、上の写真で共通しているのはウニである。ウニと言えば、こんな姿をしている。
 |
「海栗」と書いてウニと読むことが実に納得できる姿である。しかし、内面はもう少し違う。実は、ウニはドームにそっくりである。前回考えたドーム球場ではないが、ウニは実はドーム構造をしているのだ。「そんなことは当たり前じゃないか」と言う人もいるだろう。しかし、私はつい最近までそれを知らなかった。そもそも、骨があるとすら思っていなかったのである。
もしかしたら、私のようにウニの内面を知らない人もいるかもしれない(そんな人はいない、という声も聞こえそうだが)。そこで、ウニの骨の写真を示してみる。下に示すのが、色々なウニの骨だ。
 実物はとてもきれい。日本古来の木工細工のような穴がとてもきれいである。 |
これは少し前に、宇宙科学研究所の黒谷氏の実験室を見学(ただ邪魔しただけという気もするのであるが)する機会があり、そのとき頂いたものである。最初に見たときは、「目からウロコ」であった。まさか、あの針の山の下にこんな頑丈な殻が存在しているとは、思わなかった。
写真ではわからないかもしれないが、骨には小さな穴が極めて規則的に開いている。それが、日本古来のとても出来がいい木工細工のようである。光に透かしてみると、うっとりするようなきれいさである。内部に強い光源でもおけば、プラネタリウムやミラーボールみたいに細い光線を放射する、きれいなアクセサリーができそうだ。
ところで、「何故、宇宙科学研究所の実験室にウニが?」と思われる方は、WEBで検索でもかけてみると良いかもしれない。「宇宙生物学」という面白い実験分野があるものだ。
例えば、無重力の中で生物がどのような挙動を示すか、などの研究をしたりするらしい。飛行機にのってそういう実験を繰り返すわけである。遊園地のフリーファールやバンジージャンプ、そして、ジェットコースターでさえ、駄目な私には地獄のような研究分野である。
さて、上の、ウニの骨の姿はまさにドームそのもの、とは思えないだろうか? そう、似ているのだ。 そっくりなのだ。試しに、このドームなどを見れば納得できるだろう。
 |
これは、富士山頂の厳しい環境を耐えるために、極めて安定なドーム構造が用いられているのだ。三角形のパネルが組み合わさるドームハウスは極めて頑丈である。ウニも、同じように頑丈なドーム構造の骨格を持っているのである。レーダードームは富士山頂で頑張っているが、宇宙科学研究所のウニは色々なところへ連れて行かれて、厳しい実験に耐えているのである。
こういった、ドームと言えば、R.バックミンスター・フラー博士のドーム理論だろう。フラー博士とドームハウスのスケッチ図を示してみる。
|
よく、環境適応性の高さを謳うことの多いドームハウスであるが、もしかしたら、ウニがその祖先であるかもしれない。もしかしたら、フラー博士は「海の中でじっとたたずむウニの夢を見て」ドームハウスを思いついたのかもしれない。
アメリカ人であるフラー博士がウニを食べたとは思えない、という人も多いだろう。それは確かにその通りである。しかし、フラー博士はかなりの変人である。変人ならば、ウニを食べまくっていたとしても、おかしくはない。
普段は「何を馬鹿な発想だ」と思うことだろう。しかし、ドーム球場の野球を見ながら、脳みそがビールとウニで満たされてしまうと、「そうだ、フラー博士はウニが大好きなのだ!そうに違いない!」と確信してしまうのだ。
仮に、フラー博士がウニに影響されていないとしても、ウニはフラー博士がドーム理論を考えるずっと太古の昔から、ドーム構造をしていたのである。ならば、「元祖はやはりウニなのだ!」と言ってしまって良いだろう。太古から厳しい環境を耐えつづけてきたウニは、今や宇宙へ飛び出し、さらに厳しい環境の中で活躍しているのである。
1999-11-23[n年前へ]
■ミニスカートの幾何学 
32cmの攻防戦
早朝、東名高速で事故渋滞にはまってしまった。仕方がないので、TVを眺めていると、面白い話をやっていた。それは、ミニスカートの丈の話である。何でも、最近の流行はミニスカートの丈が32cmのものであるらしい。女子高生?などが言うには、
「34cmだと長いしぃ。」だから、32cmだと言うのだ。別に、オリンピック選手でもないのだから、ミニスカートの丈の限界まで挑戦しなくても良いだろう、と私などは思ってしまう。しかし、彼女たちはそう考えないらしい。人それぞれである。
「30cmだと下着が見えちゃうしぃ。」
それにしても、スカートの丈が32cmと30cmの間でそんなに、違いがあるものだろうか? 「見える・見えない」を決める分水嶺がその2cmの違いにあるものなのだろうか? 妙に不思議である。 そこで、ミニスカートの幾何学について考えてみることにした。題して「32cmの攻防戦」である。
何より先に確認しておくが、私は今回は科学的好奇心で動いているのである。そこに、一点の不純な気持ちも存在しないことを、ここで確認しておく。いや、むしろ、女性のためのミニスカート理論の構築を目指しているといっても良いかもしれない。といっても、信用されないとは思うのであるが...
 |
さて、先のTV番組によれば、腰からスカートの先までの長さを「スカートの丈」というらしい。また、先のTV番組により、「腰から下着の一番下の部分(股下を計るときの一番上)までの長さが大体25cmである」という重要な情報を得ることができた。
それでは、解析を始めてみよう。以下に、今回考えた「ミニスカートの幾何学」を示す。なお、今回使用する長さの単位は全て(cm )である。
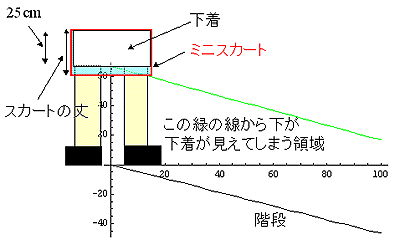 |
まず、階段の途中に立つミニスカートを履いた女性の下着中央部分とミニスカートの最下部を結ぶ直線を考える。この線よりも下が、下着が見えてしまう領域である。もちろん、階段の下には潜り込めないわけであるから、その線と階段で囲まれた領域内から見た際に下着が見えてしまうわけだ。その線のことを「下着防御ライン」と呼ぶことにする。
さて、ミニスカートの形状を考えよう、スカートの丈はもちろん入力条件としてわかる。すると、足りないパラメータは幅である。そこで、ヒップ周りが88cmとしてスカート中央から端までの長さ(rcm)を求める。2πrが88cmであるから、
r = 14cmとなる。
また、駅などの階段というと25度位だろうか。30度というとかなり急な階段である。湘南通商の階段とか急な階段は色々あるが、今回は急な階段の斜度として、25-30度位としておく。ちなみに、京都駅北口のエスカレータで実測したところ、25,6度であった。
それでは、スカートの丈が32cmで階段の角度が30度である場合の計算をしてみる。女性の股下は仮に70cmであるとしておく。おそらく、身長160cm位であれば、この程度であろう。
それでは、ミニスカートの丈が32cm、30cmの時の「下着防御ライン」を計算したものを示す。
 |  |
緑、すなわち、ミニスカートの丈が32cmの時は「下着防御ライン」は階段とほぼ平行である。それに対して、丈が30cmの時の「下着防御ライン」は、ミニスカートを履いた女性から離れるほど階段よりも上に離れていく。ということは、人間の視点位置が「下着防御ライン」を越えるということである。すなわち、下着が見られてしまうということだ。
階段と「下着防御ライン」の差、すなわち、人の目の高さがこの程度ならミニスカートの下の下着を見ることができる、というものを示してみる。
 |
32cmの丈の場合、10m(1000cm)離れても、目の高さが150以下の人しか「下着防御ライン」を突破できない。すなわち、女性は事実上「下着を見られる恐れがない」といって良いだろう。もちろん、20mとか離れたら別である。しかし、超人的な視力がなければ、そのような条件下で下着を確認することはできないであろう。
それに対して、30cmの丈の場合には6m離れた時点ですでに視点が2mの位置にある人でも「下着防御ライン」を突破できてしまう。これでは、「全ての人に下着を見られてしまう」ということになる。
もし、女性の身長が20cm程度高く、180cm程度であったら、どうなるだろうか。おそらく、股下長さは10cm程度長くなる。すると、上の図(階段と「下着防御ライン」の差)の緑、赤ラインは10cm程度高くなる。それでも、緑の32cmスカートの「下着防御ライン」はやはり安全圏といえるだろう。
また同様に、厚底サンダル・ブーツなどを履いた場合には股下長さが20cm弱高くなると考えられる。この影響を考えると、長さとしては身長の影響よりも大きいわけである。それは、身長の1/2が股下長さの増加に繋がるのに対し、厚底靴の長さはそのものずばり股下長さの増加に繋がるからである。しかし、それでもやはり緑の32cmの「下着防御ライン」は安全圏である。
すなわち、32cmと30cmのスカートの丈の長さの間には、「下着が見える・見えない」に関する分水嶺が確かに存在するのだ。先の、
「30cmだと下着が見えちゃうしぃ。」という発言は理論的に裏付けられたのである。
それでは、次に階段の角度が25度である場合の計算をしてみる。
 |
緑の線、すなわちスカートの丈が32cmの場合の「下着防御ライン」が階段にどんどんすり寄っているのがわかると思う。すなわち、「下着防御ライン」はより強固なモノとなっているのである。階段と「下着防御ライン」が女性から離れるほど近づくのである。次に、階段と「下着防御ライン」の差を見てみよう。
 |
緑線、すなわちスカートの丈が32cmの場合に注目する。 女性から、離れても、近づいても、何人たりとも、下着を見ることはできないのだ。下着がシュバルツシルト半径の中に隠されるといっても良い。女性の安全を確保する「完全安全条件」を満たす「下着防御ライン」が完成されているのだ。
これは階段と「下着防御ライン」が平行である条件を境として、そのような条件が達成される。その条件よりより「下着防御ライン」が強固になると、誰も「下着防御ライン」を突破することはできない。すなわち、「完全安全条件」が達成されるのである。
この絶対に下着を防御可能(「完全安全条件」)な「完全安全条件」とは、階段と「下着防御ライン」が平行である条件であるから、ミニスカートの丈(xcm)をパラメータとして、
Tan[階段の角度] = (x-25)/14で計算することができる。ここで、14は腰回りの半径(cm)であり、Hip88cmの人の場合である。もちろん、極端な安産体型の場合には、その14という値を適当に補正する必要がある。
さて、この条件には女性の身長(股下長さ)は関係しないところが面白い。もちろん、厚底サンダルなどを履いても同じである。もちろん、若干の影響はあるが、あまり影響はない。
さて、今回の「ミニスカートの幾何学」の考察により、判明した結果をまとめてみよう。
ミニスカート内部の下着が「見える・見えない」には
- ミニスカートの丈が30cmと32cmの間に、分水嶺が確かに存在する
- 絶対に下着を防御可能(「完全安全条件」)なミニスカートの丈(x cm)とは、Tan[階段の角度]= (x-25)/14 により決定される
- ここで、14は腰回りの半径(cm)であり、Hip88cmの人の場合である
- 極端な安産体型の場合には、その14という値を適当に補正する必要がある
- 一方、ミニスカートを履いている人の身長はほとんど影響を及ぼさない
- 厚底サンダルの方が身長よりは影響を及ぼすが、それでもほとんど影響はない
ミニスカートを身につける女性の経験に基づく、「30cmだと下着が見えちゃうしぃ。」理論はなかなか正しいことがわかる。経験というものを軽んじてはいけない、という良い?例かもしれない。結果の伴わない理論に価値はない、ということだろうか。
それにしても、厚底ブーツにミニスカートを履いた女性達は、ロールプレイングゲームの主人公達のようだ。色々なアイテムを手に入れ、冒険を続けている主人公達のようである。ほんの少しだけ、うらやましいような気もする。
さて、こういう話題を書くと少し不安がある。もちろん、私もミニスカートを見ると、妙に心が落ち着かないのも確かに事実ではある。しかし、だからといってことさらに興味津々というわけでもない、と思う。多分。ということで、「できるかな?」の女性読者の数が減少しないことを、ただ祈るのみである。
1999-12-16[n年前へ]
■スキー場の特殊相対性理論 
ジャンプの飛距離は何メートルだ?
突然ではあるが、HIRAX.NETのドメインレコードを調べてみると、
Record created on 16-Dec-1998.となっている。自分のドメインのレコードをわざわざ調べたのは、一体いつ取得したのか私自身が忘れてしまったからである。何しろ、「できるかな?」は当初異なる場所での二本立てで公開していたため、私の記憶がごっちゃになっているのである。あと各回の公開順序も実はかなりシャッフルされている。そのため、完全に忘れていたのである。
「できるかな?」はHIRAX.NETのコンテンツの一部である。しかし、HIRAX.NETの誕生日よりも、「できるかな?」の誕生日の方が実は早い。
で書いたように、「できるかな?」はすでに満一年を迎えていたわけである。そしてやっと、本日でHIRAX.NETも満一歳になったわけだ。何はともあれ、目出度いことである。子供の頃やらされた「ドリル」でも3日も続かなかったのに、1年続くとは、正に奇跡である。奇跡はそうそう続かないような気もするが... さて、関係ない話はここまでである。今回の舞台は万座温泉だ。なぜなら、先週末私は万座温泉でスキーをしていたからだ。何故だか理不尽な話しではあるが、私は万座温泉でローレンツ収縮を考える羽目になったのだ。もう少し正確に言えば、スキー場で特殊相対性理論を考える羽目になったのである。(先に断っておくが、私はトンデモ話をマジメな顔で言うことが多い。)
 |
話の発端はスキーに行く前に遡る。職場の今年の新入社員であるタカノリ君(仮名)とスキーの話をしていた。彼は秋田出身であり、子供の頃からスキー三昧の生活をしていた。大学に入り京都へ行ってからは、スキーをやる頻度は下がったが、チョコチョコ行ってはいたという。
そのタカノリ君(仮名)と話していると、彼はさりげなくこう言った。
「10m位のジャンプはよくするスよ。」10mである。2mの身長の人の5人分である。それは、スゴイ。
「えぇ、本当かぁ〜〜」
「いやぁ、そんなのよくやることじゃないスか?」
今回のスキー&温泉旅行は職場(と何故か競合他社)の人達30人程で行った。ほとんどの人は、割にスキーは好きな人が多い。従って、スキーも上手い人が多い。その人達に囲まれながら、タカノリ君(仮名)は断言した。
「6,7mは簡単だけど、10mってスゴイなぁ。」タカノリ君(仮名)、ただ者ではない。
「本当かぁ〜〜」
「えっ、だってただ飛ぶだけじゃないっスか。」
そこで、スキー場でその確認をしたわけである。場所は万座プリンスゲレンデの下部である。リフトとコースが交差する辺りに、ジャンプできる場所があったのだ。そこで、彼は軽く滑り出し、力一杯ジャンプした。
果たして、タカノリ君(仮名)は何メーター飛んだのであろうか? それとも、ただのホラ吹き男爵であったのだろうか?
ところが、その答えをすぐに書くわけにはいかないのである。なぜなら、タカノリ君(仮名)がジャンプをしてみせた時に事件は起こったのである。
「どうスか!10mはいったんじゃないスか!」
「3,4mしかいってねーぞ!おイ!」
これは、一体どうしたことだろうか? しかも、会話はまだ続くのである。
「何でっスか!軽く1秒は宙に浮いてたっスよ!」ますます不思議なことに、時間感覚すら違っているのである。一体何が起こっているのだろうか?
「そんなことはねぇぞ!コンマ数秒だろう!」
私はここで気づいたのである。観測者の間で時間と空間の不一致が生じているのであれば、ここはもちろんアレの登場である。アレと言えば言うまでもない、もちろん特殊相対性理論である。
そう、万座温泉スキー場ではローレンツ収縮を実感することができるのである。「スキー場でジャンプする」という現象を考える際には、「スキー場におけるhiraxの特殊相対性理論」を導入しなければならないのであった。
それでは、簡単に「スキー場におけるhiraxの特殊相対性理論」を説明しよう。今回、生じている不思議な現象は以下のようになる。
登場人物
- タカノリ君(仮名) 速度vでジャンプをしている。
- 観客 静止している。
| タカノリ君(仮名) | 観客 | |
| 飛んだ距離 | 10 | 3 |
| 飛んでた時間 | 1 | 0.3 |
つまり、速度vで飛んでいるタカノリ君(仮名)の感じる空間や時間といったものは、静止している観客に比べて、いずれも3倍程度に膨張しているのである。
通常の世界で生じるローレンツ収縮は、速度vで移動している観測者の空間軸も時間軸も
![]()
倍縮むのであるが(ここでは光速c=1の単位系を使用している)、
であるが、「スキー場におけるhiraxの特殊相対性理論」では、速度vで移動している観測者の空間軸も時間軸も静止している観測者に対して、逆に![]()
倍に延びてしまうのである。もし、ミンコフスキーの時空図を書いて確認しようとする人がいるならば、座標軸の傾きの変化も通常のローレンツ変換と逆に考えてみてもらいたい(その延長で考えていくと、矛盾があるというご指摘メールはノーサンキューである。)。
さて、そもそもローレンツ収縮は、マイケルソン - モーリーの実験結果(エーテルの影響が検出できない)を説明し、なおかつエーテルの存在を認めるために立てられた。それは、「運動体はすべてその運動方向に収縮する」という仮説である。その仮説を理論的に完成させたのが、アインシュタインの特殊相対性理論である(考え方としては根本的に異なるが)。
今回の話の中で「エーテル」に変わるのは、「空気」だろうか? いや、違う。私はむしろ、速度そのものであると、考える。つまり、特殊相対性理論と同じである。スピードを出して飛んでいるという感覚、速度が与える感覚の変化、すなわち速度そのものが、「スキー場におけるhiraxの特殊相対性理論」を要請するのである。
今シーズン、スキー場でせっせとジャンプをする人がいるならば、ぜひ「スキー場におけるhiraxの特殊相対性理論」について考えてみてもらいたい。
このWEBへ来る人の中で、同時期に万座温泉スキー場にいた人はいるだろうか?12/11.12に万座温泉スキー場のプリンスゲレンデの下部でジャンプにいそしんでいたのが、私達の一行である。そして、その中の一人(ショートスキーでせっせと飛び跳ねていたヤツ)はこんなことをずっと考えていたのである。
さて、実際のタカノリ君(仮名)の飛距離がどの程度であるか知りたいと思う人も多いだろう。オマエらの主観的な評価でなくて、実測定した距離を教えろと思う人も多いに違いない。
「絶対的な基準など存在しないから、そんなことは私はわからない。」と言い放ちたいところだが、タカノリ君(仮名)の名誉のために書いておく。彼が飛んだ距離は、2m弱のスキー板で4本分はあった。実は、タカノリ君(仮名)の基準が一番正しかったのである。彼は、「やるときはやる有言実行の人」なのであった。
1999-12-30[n年前へ]
■6502と並列計算とムーアの法則 
人間のクロック&スケールアップ
「物理の散歩道」を読み直していると、とある文章に興味を覚えた。
- 第五物理の散歩道 ロゲルギスト著 岩波新書
「通信を考える」の中の興味を惹かれた部分は「信号の伝わる速度と距離と処理速度の関係」を論じている部分だ。例えば、計算機は処理速度を高めるためには回路の大きさを小さくしなければならないとか、人間の頭脳の働きの速さから集団生活の広がりの限界について論じているのだ。例えば、
- 計算機の演算速度の時間スケール -> ナノ秒 = 10^-9s (クロックで考えると、1GHz)
- 人間の演算速度の時間スケール -> サブ秒 = 10^-1s (クロックで考えると、10Hz)
つまり、通信の速度が光速度であるとして、演算の単位クロックの間に通信が行われなければならないとするならば、計算機の時間・空間スケールと人間の時間・空間スケールは等しいだろう、という推論だ。
そして、さらにロゲルギストの想像は広がり、並列計算についても論じている。
計算機が東京と大阪に離れて置かれていて、通信をしながら作業をするとしたら、人間の場合にはそれと同じ条件というのはどんなものだろうか、と彼らは考える。それは、光の速度で55時間、ちょうど冥王星の軌道直径の5倍程度の空間スケールになる、と論じている。それ以上、離れた場合には演算の過程を共に行うのは無理ではないかというのである。
こういう文章を読んでいると、この文章が作られたのが30年以上前であることを忘れてしまいそうである。この人達の思索の自由さに憧れを感じてしまう。この人達は、頭の中にタイムマシンにでも持っているのだろうか、と感じてしまうのだ。
ところで、私がコンピューターをいじるようになった頃は、Apple][の時代だった。といっても、私はお金があふれていたわけではないので、XXX電子でAplle][のコンパチ基盤を買って組み立てて使っていた。その基盤上の6502は1MHzで動いていた筈だ(あぁ、I/Oの6809派vs6502派の論争が懐かしい!)。
それから20年程たち、CPUのクロックスピードは1GHzを越えようとしている。20年で1000倍である。そして、その集積度は、ムーア(GordonMoore)の法則の「半導体の性能と集積は、18ヶ月ごとに2倍になる」に従っている。
それでは、人間はどうだろうか?人間の脳味噌のクロックがどの程度であるか測定されているかどうか、素人の私にはよくわからない。しかし、WEB上のデータとしては、例えば
- Mayo's Profile( http://www.ceres.dti.ne.jp/~mayo/profile.html )
ロゲルギストの時代、すなわち30年以上前、から現在のMayo's Profileの値がほとんど変わっていないように、人間の演算スピードは変わるようなものではない。それは、そうだろう。ヒトのクロックスピードや集積度といったものは、変えるわけにはいかない。当然である。CPUと違ってプロセスルールを変化させるというような訳にはいかないのだ。
それでは、演算性能を上げようとしたらどうするだろうか?そうなると、並列計算を行うのが自然だろう。単独のCPUの性能を上げるわけに行かなくても、共同作業を行えば、演算性能を上げることができる。
現代はほとんどの作業が共同作業で行われる。また、その共同作業も大人数が関わるようになってきている。それは、どんな業種でも同じだ。一人では、なかなかできないことが多くなっている。
それら共同作業、すなわち並列計算、を行う人達(例えれば並列計算機における各ノード)を増やし、それらの間の情報転送をすばやく行うことが多くの作業(計算)を行うための手順だろう。
そこで、
で用いた- 人口増加( http://www.t3.rim.or.jp/~kabutoya/KABHTML/Yoi/2-1.html )
 |
なるほど、人間界の並列計算機におけるノード数は増加している。そして、各ノード間の通信速度を調べるために、まずは、
- 来て、見て、触って、情報伝達
- ( http://www.f-jhs.fukuoka-edu.ac.jp/3-3/jyoho.html )
西暦 内容これを全部転送速度に直してみる。といっても、よくわからない部分も多いので、私が適当に決めてみる。それでは、その変化を示してみよう。とりあえず、ここ200年位の間のものを考える。
-4000 のろし
-2400 伝書鳩
-2300 馬による伝令制度
1837 モールス電信機
1876 ベグラハム=ベル電話機
1909 グリエルモ=マルコーン無線電話機
1973 Ethernet XeroxPARCで生まれる。(ちなみにEther=エーテル)
1979 DIX規格=10Mbps
1992 FastEthernet=100Mbps
西暦 内容という感じだ。グラフにすると、
1837 モールス電信機 = 2bps
1909 グリエルモ=マルコーン無線電話機=10kbps
1979 DIX規格=10Mbps
1992 FastEthernet=100Mbps
 |
こんな感じである。対数グラフにおいて直線的に情報伝送速度が速くなっている。この関係は結構きれいである。
別に意図してこういう数字にした訳ではないのだが、不思議なことである。
このようにして、人間(ノード)間の転送レートが高くなることにより、先のような人口増加に伴うトラフィック増加をしのぐことができていると考えることもできるかもしれない。そして、人間達の共同作業、すなわち並列計算、を行うだけのバススピードを確保しているのである。
最近、会社組織などで分社化とか事業分割とかの話題をよく耳にする。こういった時に、分割における時間と空間のスケールはよく考える必要があるだろう。分割が有効なのは、ほとんど独立なものを分割する場合のみである。並列計算における領域分割などと同じだ。
共同作業がほとんどなく、結果のみをやりとりすれば良いような場合には分割による効果はあるだろう。その一方で、同じ事業・作業を行っているところが、離れていては作業の効率は上がらない。もし、技術系の会社でそのようなことを行うのであれば、事業や部署を並列化した際の真面目なシミュレーション位は行うべきだろう。いや、別に深い意図はないけど。
こういったことは「新・闘わないプログラマ No.109 時代錯誤」に書かれていることとも少し似ているような気がする。
さて、1999/12/30-2000/1/1は野沢温泉で温泉&スキーである。2000年問題で会社に泊まり込む人も多いが、私はスキー場で泊まり込みである。同時期に野沢温泉に行く人がいるならば、ぜひ一緒に「スキー場の特殊相対性理論」について討論したいと思う(スキー場で)。
2000-02-06[n年前へ]
■パノラマ写真と画像処理 Pt.1 
パノラマ写真を実感する
「パノラマ」という言葉は何故か大正ロマンを感じさせる。かつて、流行ったパノラマ館や江戸川乱歩の「パノラマ島奇譚」という言葉がそういったものを連想させるのだろう。私も自分で写真の現像・焼き付けをしていた頃は、フィルム一本まるまる使ってベタ焼きでパノラマ写真を撮るのが好きだった。
そういう癖は持ち歩くカメラが「写るんです」と「デジカメ」へ変化した今でも変わらない。例えば、
の時に撮ったこの写真もそうである。 |
そしてまた、次に示す写真もそうだ。これは1999年夏頃の早朝に箱根の湖尻で撮影したものである。360度のパノラマを撮影したものだ。
 |
観光に行った先で撮影したと思われるかもしれないが、残念ながら違う。出勤途中に撮影したものである。豊かな自然がありすぎて、涙が出そうである。
パノラマ写真としては、こういう景色を撮ったものも良いが、人が写っているものも良い。私の勤務先がこの大自然の中に移転してくる前、都会の中にあった頃に居室で撮ったパノラマ写真などはとても面白い。窓の向こうにはビルが見えたり、周りに写っている人ですでに退職した人が何人もいたりして、涙無しには見られない。
もちろん、こういった写真はパノラマ写真で楽しむのも良いが、もっと実感できるものに加工しても楽しい。私がかつて都会の居室で撮影したものは、当時はAppleのQuicktimeVRのムービーファイルに変換して遊んでいた。今はもうない居室の中をグリグリ動かすのはホロ哀しいものがあり、とても味わい深かった。
ところで、WEB上でそういうパノラマのVRファイルを見せるにはどうしたら良いだろうか?もちろん、AppleのQuicktimeVRを用いれば良いわけではあるが、プラグインが必要である。私はQuicktimeは好きであるが、ブラウザーのQuicktimeのプラグインは嫌いである。WEBを眺めているときに、「Quicktimeのアップグレードはいかがでしょう?」というダイアログが出ると、少しムッとしてしまう。そこで、Javaを使うことにした。いや、もちろんJavaをサポートしていないブラウザーもたくさんあるが、こちらの方がまだ好きなのである。
そのようなパノラマのVRを実現するJavaアプレットには、例えば
- Panoramania
- http://www.lamatek.com/lamasoft/Panoramic/test.html
- Javaアプレット(パノラマver1.1)
- http://village.infoweb.ne.jp/~fwbc6098/java/panorama/panorama.htm
- TheVRApplet1.0
- http://www.physik.uni-greifswald.de/~jonas/VRApplet/VRApplet.html
- how toinsert the panorama show (java applet) inside your home page ?
- http://persoweb.francenet.fr/~carl/brique/exapano1.htm
さて、ここまでは単なる前振りである。本題は、実はこれから始まる。先日このようなメールを頂いた。
私はWindowsを使っているのですが、AppleのQuicktimeVRに興味があって、QuicktimeVRのパノラマ・ムービーを作っています。しかし、素材となる画像の作成に四苦八苦しております。ご承知の通り、
- ライカ版カメラに24ミリ広角レンズをつけて、
- 三脚にパノラマヘッドをつけて、ぐるりと周囲を12枚撮りして、
- 現像、プリントし、
- スキャニングして、ステッチャソフトでレンダリングし、
- それをMacintosh上でMake-QTVR-Panoramaにドロップして、
- 8ミリビデオに広角レンズを付け、
- 90度横倒しにして、10秒程度で1回転するようにステッピングモーターで駆動するパノラマヘッド(自作)に乗せ、
- 高速シャッター撮影し、
- マックのAV機能で円周12枚の静止画を取り出
- し、
- 8ミリビデオを横倒しにして、
- モーター回転するヘッドでぐるりと360度撮影し、
- その撮影した動画ファイルの、各フレームから走査線にして数本分を抽出し(インターレースで256本のうちセンター128本目の前後数本の走査線分)、
- それを貯めて1枚のjpgファイルにする、
- そのJPEG画像をMakeQTVRPanoramaの入力にして、パノラマムービーを作る、
その場合には、スリットスキャンカメラを入手し、それをカラープリントする設備を準備すればいいのでしょうけど、高価です。
そこで、
長々と分かりにくいことを書きましたが、要は、「マックで動く電子スリットスキャンソフト」をなんとか作っていただけないでしょうか?もし、そのようなソフトがあれば、
まずは、答えを先に書いてしまおう。私が作らなくても、
- NIH-Image (MacOS)
- ScionImagePC (Windows)
- 複数画像(動画)からの走査線抽出
ScionImagePCの動作画面を以下に示す。NIH-Imageとほぼ同じである。
 |
これらのソフトのStack-Slice機能を用いれば「複数画像(動画)からの走査線抽出」ができる。その使用例と、その面白い座標軸変換について考えてみたい。しかし、このページは少々重くなってきた。まして、走査線の抽出の話は使用画像が多くならざるをえない。そこで、次回、詳しく使用例を紹介することにする。よく、次回といったまま数ヶ月経つことがあるが、今回は大丈夫である。少なくとも数日後には登場することと思う(多分)。
あれっ、ここまで書いてからinfoseekで検索すると、
- パノラマ写真のひっみっつっ!
- http://www.imagica.com/nomad/sig98/hitachi/

