2002-02-20[n年前へ]
■「やおい」の評価演算子 
ベクトルの彼方で待ってて II
 東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか?
東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか?
「福田X小泉っていうのは、結構上手くやっているのかな?」と私が言うと、おもむろに
「あれは、福田X小泉じゃなくて、絶対あれは小泉X福田なのー」とその記者が言ったのである。何を言っているのかその意味がよく判らないまま、「ん〜?」と私が首を傾げていると、繰り返し
「福田X小泉と小泉X福田は全然意味が違うのー」と言い始めるのである。何が何だか訳がわからない。じゃぁ、何か?小泉X福田だと小泉純一郎が総理大臣で福田康夫が官房長官だけど、福田X小泉だと福田康夫が総理大臣で小泉純一郎が官房長官になるとでも言うのか??政治の世界では、言う順番で総理大臣が決まるとでも言うのか?と私が口をはさむと、
「そう。ただ、ちょっと政治の世界とは違う世界かも〜。政界じゃなくて、やおい界ではー。」と言うのだ。なんだコイツ?政界は判るけど、やおい界って一体何処の世界の話だ??と、困惑する私も構わず、そこから延々と長い演説が始まった…。その大河ドラマのようにやたらと長い話を要約すると、
- やおい → 一部の女性が好む「男性同士の恋愛もののストーリー」のこと
- X → やおいの世界で恋愛の関係を示す記号。例えば、AさんとBさんが恋に落ちるであれば、Aさん×Bさんと表す。で、ここで重要なのは先に位置する方が「攻め役」となって、後に位置する方が「受け役」となる…。つまり、例えばサド侯爵とレオパルド・マゾッホであれば攻め役がサド侯爵で、受け役がマゾッホなので、サド×マゾなのである。決して、マゾ×サドではない…
で、日本酒を飲みながら、まだまだ続くその話に悪酔いしていると、「カップルの順序が重要なんだー」という言葉を聞いて、ふと中学の頃の数学の授業を思い出した。その頃、大学を出てまだ一年目の斉藤慶子似の数学の先生と話していたときに、「Hくん、あのね掛け合わせる順序が違うと結果も違っちゃう計算もあるのよ」と教わったことがあった。そんな言葉から私は未知の「数学の世界」をかいま見たりしたのである。 今考えてみれば、新任の斉藤慶子似の女性教師の個人授業なのだから、行列・ベクトルの掛け算の順序なんかじゃなくて、「もっと違う順序」を手取り足取り教えてくれても良かったんじゃないか、とか思ったりするし、そうすれば、私は未だ見ぬ「大人の世界」を覗き見ることができたのではないか、と思ったりもするのだけれど、そんなことは残念ながら無くて、私はただ「行列・ベクトルの世界」を覗いただけだったのである。
で、そんな昔話を思い出したせいか、頭の中でこんな風に思ったのである。そういえば、これまで「できるかな?」では数多く「恋の力学」でも遊んできた。ただ、そこでは「惹かれ合う恋心の大きさ」だけに注目して、そのカップルの中での役割などは考えたことがなかった。そこで、今回は「やおい」のカップルの「役割・順序」に注目し、その「役割・順序」を評価する演算子を行列・ベクトルの掛け算になぞらえながら考えてみることで、これまでと同じく色々な「恋の形」を眺めてみたいと思う。
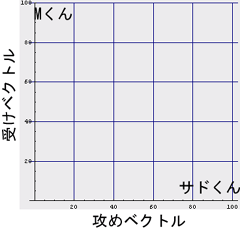
まずは、色々な人物(実際の人物であったり、小説などの登場人物であったり)のタイプを二次元空間に配置しよう。「この人は結構攻め役が合いそう」とか「この人は絶対受け役が合うのだー」という適性を
- 攻めベクトル
- 受けベクトル
 |
そして、カップリング適性では「A×B、B×Aが全然違う」ということから、外積(ベクトル積)をそのまま流用して、適当な評価関数を作ってみるのが自然だろう。まず、
カップリング適性ベクトル = (攻め度(s)、受け度(m))と表記して、例えばAさんのカップリング適性ベクトルを(As, Am)と表すことにしてみよう。すると、Aさんが「攻め」でBさんが「受け」のカップリング適性は、この二人の適性ベクトルのベクトル積として表すことができる。つまり、
A×Bのカップリング適性 = ( As * Bm - Am * Bs )となるわけである。式を眺めれば判るように、Aさんの攻め度が高くて、Bさんの受け度が高ければ、この評価関数は高い値を返す。つまり、「A×Bの順序は正しいのだー」という評価を返す。つまり、「A×B」はなかなか良いカップルだー、と教えてくれる。また、もしAさんの受け度が高くて、Bさんの攻め度が高ければ、低い値を返す。つまり、「A×Bの順序は絶対間違ってるのだー」と評価してくれるのである。なんともありがたいことに(いや別にありがたくはないか…)、この「やおいのカップリング評価演算子」が「福田X小泉」と「小泉X福田」のどちらが自然なのかを教えてくれるのだ。試しに、上のサドくんとMくんであれば、「サドくん×Mくん」= (100,0)×(0,100) = 100*100 - 0*0 = 10000でとっても「良い感じ」でああるが、「Mくん×サドくん」= (0,100)×(100,0) = 0*0 - 100*100 = -10000で「このカップリングは絶対順序が違うー」と判るわけである。
= Aさんの攻め度 * Bさんの受け度
- Aさんの受け度 * Bさんの攻め度
とりあえず、今回はこの評価演算子を作成するところまでで終えたいと思うが、いずれこの「やおいの評価演算子」を武器にして、いつか(?)「やおいの世界= やおい界」に限らず、色んな数多くの恋の関係を目に見えるようにしてみたいと思う。そして、これまで数多く考えてきた「恋の〜シリーズ」を充実させていきたいと思うのである。
ところで、今回のカップリング適性評価演算子は基本的に外積そのものである。つまり、この演算が返す値は「二人のベクトルでできる平行四辺形の面積」に等しい。つまりは、「二人のベクトルでどれだけ色んな違うことがきでるか」を示す尺度である。そして、その値は二人のベクトルが直交する時、すなわち二人のベクトルが重ならず独立である時に最大値となる。つまりは、「二人のベクトルが違えば違うほど大きく」なる。例えば、先の「サドくん×Mくん」であれば二人のS,M趣向が完全に正反対であったからとてもお似合いのカップルになったのである。
これをいわゆる恋の話で考えてみると、とっても独立な二人、趣味が重ならない二人がお似合いだということになる。なるほど、そんなカップルも世の中にはたくさんいることだろう。そんな人達を「外積タイプのカップル」と呼ぶことができると思う。
一方、趣味が重ならないカップルだけでなくて、世の中にはそれとは正反対の「趣味が重なる良いカップル」も数多くいる。それは「内積タイプのカップル」である。内積はA,Bベクトル間の正射影に比例する量であって、つまりは「二人の重なるベクトルの大きさ」である。それは例えば、相手の中に自分を重ね合わせるような「二人の重なる部分が二人を結びつけるようなカップル」なのである。
「理系と文系」・「男と女」が対極的なものでも、相反するものでもないのと同じく、「外積カップルと内積カップル」も別に二つに分けられるようなものではないだろう。「外積タイプの恋」も「内積タイプの恋」が混じり合って、それぞれに良いところもあれば、危ういところもあって、などと想像してみるのも面白いに違いない。そして、さらにはもしかしたらベクトル空間で萌えることができるようになったりするかもしれない。
そういえば、ふと考えてみると以前「恋の形を見た人は」で最後に引用した本橋馨子の「兼次おじ様シリーズ」は男性同士の恋の話だった。つまりは「やおい」の話だった。そこで、もう一度そのセリフを最後に飾って眺めてみようと思うのである。
「愛はどんな形をしているか知っているか?」「見た事ないからわかりません。」「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...
もし愛に優劣を決めるものがあればなんだろう?... 異性愛か、同性愛か、そんなものじゃない …たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」
2002-06-03[n年前へ]
■カードサイズの「画像探偵セット」!? 
お手軽線数メーターを作るのだ
「どんなものでも、自分の目で眺めてみた〜い」と、ワタシはいつでも思う。世の中スベテのものを、自分の目で眺めてみた〜いと思う。しょんべん小僧が空中に描き出す放物線、巨乳ギャルにロックオンするオッパイ星人の目の動き、ビデオにかかるモザイクの向こう、はたまた田代まさしが恋い焦がれるミニスカートの結界の秘密、とにかく世の中のものスベテを何でもかんでも眺めてみたい、覗いてみたい、とワタシはいつも思っているのである。(とはいえ、誤解されると困るので念のために書いておくが、もちろんミニスカートの中を覗いたりはしないのだ)
そんなわけで、ワタシのケータイのストラップには「ちっちゃなちっちゃな虫メガネ」がついている。この虫メガネを武器にして、ワタシは色んなモノを覗くのがクセになっている。スーツ姿で出張している時だって、おもむろにこの虫眼鏡を取り出して、色んなものを覗いてみたりしているのである。
 |
だから、毎朝届けられる新聞に折り込まれているチラシやカタログを眺めるときだって、そんなカタログに「ちっちゃなちっちゃな虫メガネ」を向けてみて、その「虫メガネ」を通して、カタログがどんな風に印刷されているかをよく眺めてみる。下の左のようなカラーの綺麗なカタログだって、「虫メガネ」を通して眺めてみると、右の拡大写真みたいに、四色(シアン、マゼンダ、イエロー、ブラック)が規則正しく並んでいるようすが見えてくるのである。離れてみればキレイな写真が「虫メガネ」を通して眺めてみるだけで、こんな風に様子が変わるなんてとても不思議な気分になったりするのである。まるで、女性の化粧のように不思議で、こんな四色の手品はとても面白いのである。
| (左上と右上部分はマゼンダとシアンだけを見やすくしてみた)
|
で、こんなカタログの拡大図を眺めていると、四色に分けられた色がどんな風に並べられ形作られているかを、知りたくてたまらなくなったりする。つまり、「どんな間隔でこの色は配置されているのだろう?」とか「一体、どんな角度でこの色は並べられているのだろう?」とか思うわけである。もちろん、この画像に二次元フーリエ変換などをかけさえすれば(周波数解析をすれば)、「どんな角度で・どんな間隔で色が並べられているか」ということは知ることができるけれど、まさかワタシの頭の中でそんな作業ができるわけはない。かといって、このカタログを読み込むための「画像読みとり装置」や「解析をするためのコンピューター」を毎日持ち歩くなんてこともできるわけもない。
そこで、「どんな間隔でこの色は配置されているのだろう?」とか「一体、どんな角度でこの色は並べられているのだろう?」とかいう疑問の答えがすぐ判るように、先日こんなカード、ぴったりクレジットカードサイズの透明シートに規則的なパターンを印刷したカード、を作ってみた。名付けて、Peco-Chartなのである。
これはもちろん、判る人には判るだろうが、ハンディ「線数メーター」というモノである。一言で言えば、画像の周波数解析をとっても簡単にすることができる手品の小道具のようなカードなのだ。
 |
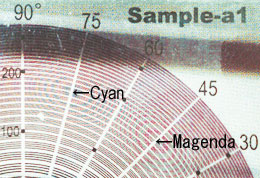
例えば、さっきのカタログの上にこのPeco-Chartを重ねて置いてみると、アラ不思議、何やらヘンな模様、不思議なモアレ模様が浮かび上がってくる。下の左の写真、あるいは右の拡大写真を眺めてみればマゼンダとシアンの同心円がハッキリと浮かび上がっているのが見えるだろう。例えば、シアン色の場合は75°の角度で175線(175線/inch)位の位置、そしてマゼンダ色の場合は45°の角度で同じく175線位の位置を中心として、同心円状のモアレ模様が浮かび上がっている。
つまり、「このカタログはシアンは75°の角度方向に1インチ辺り175個のドットが並べられていて、マゼンダのドットは45°の角度方向に並べられている」、ということを、このPeco-Chartを重ねて置いてみさえすればたちどころに知ることができるのである。
 |  |
 |
こんなペラペラのカードで周波数解析ができるなんてとても不思議に思えたりもするけれど、ちょっと考えてみればこれはごく当たり前の話である。
でも似たようなことをしたように、モアレというものは「二種類以上の何らかの模様(パターン)が干渉して発生する」ものである。つまり、ある意味「二つのパターンの相関をとる」ということである。そしてまた、少し考えてみれば「画像の周波数解析」というものは「対象となる画像」と「基準関数(三角関数etc.)」の間で相関を調べることと同じである。だから、「基準となるパターン」を「対象となる画像」の上に重ねてみた時に見えるモアレのパターンは「対象となる画像」の周波数解析結果を実は示していると考えてみても良いのである。だから、このPeco-Chartはクレジットカードサイズのペラペラなちっぽけなヤツではあるのだけれど、実は色んな画像の周波数解析をしてくれるスゴイヤツだったのである。そして、こんなポケットに入るほど小さい線数メーターははなかなか無いので、、カード入れからコイツを華麗に取り出してみせたりすると、うらやましがる人もとても多く(仕事柄、画像出力に関わる人達が多いから)、なかなかに気持ちが良いのである。 とはいえ、自慢してばかりでは何なので、さらに大量に配布すべく新たなPeco-Chart二号機をデザインしてみた。それが、下の名付けてPecochartproである。
 |
このPecochartproの謳い文句はその名の通り「プロ仕様」というわけで、画像出力に関わっている何人ものベータテスター達(自分も含めて)の感想をもとにして、
- 70線から350線までの線数とスクリーン角度の測定ができる「線数・角度メーター」(分解能を2線単位から1線単位へと二倍向上、スクリーン角度のガイドは2.5度刻み)
- 90線から410線までの線数を高精度(0.25線刻み)に計測することができる「線数メーター」(新機能)
- 線・文字の太さを計測できる「線幅スケール」(新機能)
- 〜30級、〜30ポイントまでの文字サイズ(級数、ポイント)測定ができる「文字スケール」(Peco-Chartと同じ)
- 「8cm定規」(Peco-Chartと同じものを使い勝手はそのままにコンパクト化)
- そして、便利な「画像に関する換算表」(内容を従来比75%増量)
それにしても、何か自分に役に立つツールを作るというのは本当に楽しい作業だった。手作りツールぎゃらりい脇色彩研究所ではないけれど、こんな「hirax.netオリジナルグッズ」をいっぱい作って「探偵セット」ならぬ「できるかな?セット」として、面白メールをくれた方にプレゼントとかしてみたら楽しいんだろうなぁ、と思うのである。というわけで、そんなツールをせっせと作るのだぁ、なんてことを実は計画中なのでした、ハイ。
2002-10-26[n年前へ]
■世界を映す玉手箱 
掌の上の不思議な世界
先日、人工衛星から撮影された夜の地球を眺めてみた。そんな夜の地球で輝いている「街の灯」を眺めていると、そんな宝石のような地球を自分の掌の上に載せて眺めてみたくなる。夜の「街の灯」できらめいていたり、人が住んでいるのに真っ暗だったりする、そんな小さな地球を作ってぼんやりと眺めてみたくなる。
そういえば、一年近く前に「小さな掌に未来の地球儀をのせて」でメルカトル図法の地図画像から正二十面体展開図を作成して、小さな正二十面体の地球儀を出力するソフトウェア"Icosahedron"を作ったことがあった。このソフトとプリンターがあれば、色んな地図から掌に載る小さな地球を作ることができる。そして、自分の掌の上で小さな「夜の地球」を眺めてみることができる。
 |
そういうわけで、夜の地球の画像を"Icosahedron"で読み込んで「小さな正二十面体の地球」を作ってみたのだけれど、その作業の途中で"Icosahedron"をいじって、
- うっかりミスのバグ修正(メルカトル→正二十面体展開図変換が間違っていた)
- のりしろ部分をきちんと描くようにした
- ソフトから直接印刷もできるようにした
- Susieプラグインに対応
- Icosahedron (2002.1026) Windows版 429kB(Linux版公開時のお知らせは"いろいろ"の方で…)
ところで、地球を中心にして地球を全周囲から眺めた様子を二次元に投影したものが地図だけれど、その全く逆のことをしたものがある。それはパノラマ写真である。何故なら、パノラマ写真は「世界の何処か一点を中心として、その点から全周囲を眺めた様子を二次元に投影したもの」であるからだ。つまり、「何処かを周囲から写したものが地図」で「何処かから周囲を写したものがパノラマ写真」であるという違いだけで、その二つはほとんど同じものだ。だから、パノラマ写真を元にして、Icosahedronで正二十面体を作ってみても、ちゃんとした世界ができあがる。
例えば、パノラマ写真を元にして、"Icosahedron"で「とても巨大な正二十面体の展開図」を作って、景色が印刷された面を内側にして「人が入れるほどの巨大な正二十面体」を作ってみれば、それは即席のパノラマ上映館となる。そしてまた、逆に景色が印刷された面を内側にして「小さな正二十面体の展開図」を作って組み立ててみれば、それは周囲を全ての景色をまるで鏡のように映し出す不思議な水晶玉のようなものができあがることになる。外に向かって「何処かから見た外側の景色」を映し出す不思議な水晶玉ができあがることになる。
結局のところ、数学的に言えば「巨大なパノラマ館」と「小さな水晶玉」の違いは曲率の符号が反対、というだけである。「巨大なパノラマ館」の場合は曲率がプラスで「世界が閉じて」いて、「小さな水晶玉」の場合は曲率がマイナスで「世界が開いて」いて、そして「正二十面体の展開図」の場合は曲率が0で「世界が平坦」だというだけの違いにすぎない。だから、「巨大なパノラマ館」はその中に向かって「何処かから見た外側の景色」を上映しているけれど、「小さな水晶玉」の場合はその外側に向かって「何処かから見た外側の景色」を上映している、ということになる。「巨大なパノラマ館」を"insideout"にひっくり返してみれば、世界が開かれた「小さな水晶玉」に変身するというだけだ。
以前、「箱根の湖尻から眺めた早朝の世界」をパノラマ写真にしたことがあったが、試しにこのパノラマの景色を映し出す小さな水晶玉を作ってみよう。
 |
上の「箱根の湖尻から眺めた早朝の世界」を閉じこめた「小さな正二十面体」が下の展開図だ。これを組み立てさえすれば、小さな正二十面体の中に「ある場所から眺めた世界」が映し出されることになる。ちょうど、透き通った水晶玉を通して色々な場所からみた景色を眺めるように、この小さな正二十面体を覗けば「箱根の湖尻から眺めた早朝の世界」を眺めることができる。
 |
そしてまた、小さな正二十面体に閉じこめることができる世界はパノラマ写真に限らない。例えば、「自分の周囲を描いた絵画」であっても構わないだろうし、あるいは「自分が描いた何か」であっても良いと思う。そんなものを小さな水晶玉に閉じこめてみれば、その水晶玉は「自分の描いた世界」を外側に向かって映し出し始めるのである。
例えば、エッシャーの「夜と昼」を正二十面体の世界に閉じこめてみたのが、下の展開図だ。これを組み立てれば、エッシャーの描いた世界が、エッシャーの描いた「昼と夜」が小さな正二十面体の中から映し出されることになる。これを組み立てた正二十面体を覗いてみれば、不思議なエッシャーの世界を色んな方向から眺めることができるのである。
 |
こんな風に、色んな画像から色んな「世界を映す玉手箱」を作ってみて、例えば「何処か旅先で撮った写真」や、例えば「誰かと撮った集合写真」や、例えば「自分の描いた落書き」や、色んな何かで小さな正二十面体を作ってみれば、きっと何か世界を写す小さな玉手箱ができあがると思う。その人だけの「その人の世界」を外に向かって映し出す小さな水晶玉ができあがるに違いない。正二十面体に閉じこめられた、だけど外に向かって開かれた、そんな世界を眺めてみるのはきっととても面白いことだろう。
もしも、あなたがそんな小さな正二十面体を作ってみたなら、ぜひぜひその「世界を映した玉手箱」を写した写真を私にも送ってもらえるとうれしいです。そんな小さな世界の展覧会も開いてみたい、ですしね。
2002-11-27[n年前へ]
■画像の二次元ヒストグラムを作るソフト 
画像二次元ヒストグラム・ソフトです。Bitmap画像を読み込んで、Red, Green, BluチャンネルのいずれかをX軸、いずれかをY軸にとります。で、二次元ヒストグラムを作るソフトです。256個以上同じ(x, y)点があればサチります。自分用にここにメモして置いておこ。
2003-02-02[n年前へ]
■モーニング娘。でクラスタ分析 
グラフ理論で今日からあなたもプロデューサー
昔からワタシには「手を抜くために色々とクダラナイことをする」という悪い癖がある。しかも、そのクダラナイことをした結果、必ずと言っていいほどに結局のところ苦労が増えまくるという結果になるのである。いわば、ドラえもんの「のび太」がいつもドラえもんの便利な道具に頼り、しかもその道具にしっぺ返しを必ず受けてしまうのを地でいくタイプなのであった。いつも、ワタシは手を抜くための道具を色々と作り、そして必ずそのしっぺ返しを食っていたのである。いわば、ドラえもんののび太とドラえもんを一人二役でマッチポンプのように演じ続けてきたのがワタシのこれまでの人生だったのである。
最初に記憶に残っているそんなワタシの悪い癖は小学生の頃のことだ。生徒会か何かでワタシは募金の集計をしなければならなかったのである。1000人を遙かに超える生徒がせっせと集めた募金なのだから、硬貨にしても膨大な枚数だった。といっても、ほとんどは一円玉とか10円玉だったのだから、それほどの金額ではなかったのだろうけれど、とにかく膨大な枚数だったのである。
そこで、ワタシは「ここは硬貨の重さを量って、金額を計算してみるのはどうだろうか?」と提案してみたのである。各硬貨の一枚当たりの重さは判っているわけだし、各硬貨に分けた上で全部の重さを量ってそれで金額に換算しちゃえば楽じゃないの、と提案してみたのである。ゼニ勘定に疲れていた周りの人々もその提案に喜び、「重さの誤差はどのくらいあると思う?」などとガヤガヤと計算しながら、みんなでせっせと硬貨を袋に入れて重さを計り始めたのである。
そして、机の上に重さを量り終わった硬貨の袋が何袋も並ぶ頃、そんな小さな銀行泥棒たちが盗んだお金を袋に入れてる最中のような様子を小学校の先生が発見してしまったのである。そして、当然のごとく私たちは先生にこっぴどく怒られたのである。「みんなが苦労して集めたお金のありがたさが判っていない」と当然のおしかりを強く強~く受けたわけである。「算数の問題解いてるんじゃぁないんだから!」とこっぴどく怒られたわけなのである。結局、私たちは硬貨の袋から硬貨を取り出して一枚一枚数え直すことになったのであった。もちろん、他の人をそそのかしたワタシに対する周りの視線は非常にキツく、ワタシの疲れも倍増したのであった。最初から硬貨の数を数えた方がよっぽど楽だったのである。
大人になってしまったワタシは今だにそんな「手を抜くための道具」を作り、そしてしっぺ返しを食らい続けている。三つ子の魂百まで、というわけなのであるが、今回は少し前にやってしまったそんな失敗を反省を含めて書いておこうと思う。
ワタシは仕事の上で色々な調査をしなければならないことがある。例えば、他のライバル会社がどんなことをしているかとか、あるいは、もっと詳しくライバル会社の中の人たちがどんな風に繋がっているか、とかを調べなければならなかったりすることがある。色々な発表資料を読んだり膨大な数の特許を読んだりして、そこに登場してくる人たちの関係を調べて、色々な推定をしていかなければならない。そのためには、たくさんの書類を調べなければならないわけで結構これがシンドイ作業なのである。
で、ワタシはこう考えたのだった。数百件もあるいは数千件も色々なものを読んで、その中に登場する人たちの関係を推定するなんてツライから、「たくさんの文書を勝手に読んで、勝手にその文章からライバル会社の中の人の関係を推定するソフト」を作っちゃえ~、と思ったのである。手を抜くためのクダラナイことのためには、苦労をいとわないワタシはそんなゴリゴリゴリゴリ真面目にそんなソフトを作ったのであった。「たくさんの文章の作者を調べ、その共著の関係から著者間の関係を調べる」というそんなソフトをせっせと作ってみたのである。そして作った後は、もちろんソフトのテストをしてみよう~、ということになった。
じゃぁ、そのサンプルデータは何を使ってみようかなと考えている時に、頭の中のどこかでモーニング娘。の「ここにいるぜぇ!」が流れ始めたのである。そこで、ワタシはモーニング娘。を含むハロープロジェクトを他社に見立てて、これまでに発売されたCDに参加している頻度・関係性等から、ハロープロジェクト内の「それぞれの人の配置」を調べてみることにしたのであった。
というわけで、つんく率いるハロープロジェクト関連で発売されているCDの枚数(なんと80枚以上だ!)に驚きながらも、CDに参加しているメンバーのデータをソフトに流し込んで、適当な各メンバーの関連性を示す数値を計算した上で、まずは各メンバーを近いものに分けるために、クラスタ分析してみた。ここで、解析ソフトは各CDに誰が参加しているかだけを知っていて、「モーニング娘。」とか「タンポポ」とかのグループが結成されていることは知らないのであるが、とにかくハロープロジェクトの中の各メンバーの「組織図」が判るわけだ。(ちなみに、ここでは似通ったものを樹形図(似通った度合いを示すグラフ、会社で言えば組織図みたいなもの)として表示するために、「Excelアドイン工房」のクラスタ分析アドインを使っている。)
まずは、前半41作のCDから推定したハロープロジェクトの中の各メンバーの関係性を示したのが下のグラフである。
 |
この樹形図グラフを眺めれば、(CDのカップリングから判断される)で誰と誰が結構近い関係にあるか、というようなことが判るハズである。といっても、このグラフでは色々なメンバーが参加したアルバムもあるいは一つのグループだけが歌うシングルも同じ重みで計算していたりするので、モーニング娘。あたりのファンの感覚からは大きくずれるかもしれないけれど、とにかくこんな「組織図」が計算されるのである。
上の前半41作から計算した樹形図の方は結構シンプルなものなのだけれど、次に示す後半41作のCDから推定した後半41作のCDから推定した各メンバーの関係性の方はもう少し複雑だ。組織的にライバル会社ハロープロジェクトは前半より複雑になってきているのである。
 |
こんな感じで、他社(ここではハロープロジェクトをそれに見立てたが)の発表資料(特許とか製品報告とか)からこんな各メンバーの組織図を示す解析ソフトを作ってみたわけなのだけれど、これではどうも不十分なのである。どうしてかといえば、各メンバーの結びつきがこの樹形図ではどうしても判りにくいのである。こんな風に各メンバーが一次元に並んでいる図ではどうも今ひとつ判らないことも多いのである。そこで、ワタシはさらに「各メンバーの結びつきを示す二次元グラフ」を出力することにしたのである。誰と誰がどのくらい近い関係にあるかなどを判りやすく表示させてみたのだった。そんなサンプルを少ないデータで表示させてみたのが下のグラフだ。モーニング娘。のメンバーの関係が判りやすい?グラフになっているのが判ると思う。
このグラフ上で各メンバーを動かせば、「飯田をこっちへ持っていけばどうなる?あー、安部がそっちへ行っちゃったよー。どうするー?」というような具合で、各メンバーの配置やプロジェクトのメンバー編成などを実験することができるのである。グラフ理論で今日からあなたもプロデューサーなのである。グラフぐりぐりで、今日からあなたもつんくなのである。グラフ配置で誰でもつんくの気持ちになれるのである。
という感じで、ソフトのテスト(になっていたのだろうか?)を終えたワタシはライバル会社の組織図を作ったのである。で、それを使いながら「この人たちはきっとこんな感じの組織になっているんですよー。そして、こんな感じでその組織は変化していったんですよー」なんて報告をしたのである。すると「おぉー、これは結構使えるかもー、なかなかスゴイぞー」となかなかに良い反応だったのである。
そこで、さらにワタシは調子に乗って「ライバル会社の各メンバーの結びつきを示す二次元配置グラフ」の方で「この人をこっちに近づけるとこの人がこっちへー、これがライバル会社の人間関係なんですよー、ほらほら~」と見せたりすると、もうこれが「おぉぅ…? …これは何て言ったら良いのかなぁ…?スゴイ…んだけどなぁ……」と逆効果どころじゃなくもう引きまくりだったのである。そして、引いてしまった引き潮をもうどうにもすることもできないままに、結局そのグラフはお蔵入りしてしまったのであった。結局のところ当たり前のようにワタシはたくさんの書類をせっせと読まなければならなくなったのである。いつものように、手を抜くために色々とクダラナイことをして、結局のところ作業量は全然減らなかったのである。昔の小さな銀行泥棒の根性は全然直っていなかったのである。のび太とドラえもんの一人二役マッチポンプ人生はまだまだ終えられそうにないのが、ちょっと哀しい今日この頃、なのである。

