1999-02-28[n年前へ]
■分数階微分の謎 
線形代数、分数階微分、シュレディンガー方程式の三題話
分数階微分?
InterLabの1999No.5を読んでいると面白い記事があった。いわき明星大学理工学部の榊原教授の「Waveletと数式処理ツール」という記事である。といっても、興味を持ったのはWaveletのことではない。もちろん、Waveletに興味がないわけではない。この榊原教授が講師を務めたWavelet講習にも参加したこともある。しかし、今回興味を惹かれたのはその記事中にあった「分数階微分の解析」である。InterLabの榊原教授の記事を引用すると、-通常微分・積分は整数回実行できるが、分数階微分はこれを分数に一般化したものである。さまざまな物理や工学の現象の記述に使われるようになった-とある。一階微分とか二階微分というものはよく使うが、0.5階微分などというものは使ったことがない。どのようなモノなのかさえよくわからない。
参考:
一体、どんな物理や工学の現象の記述に使われているのか知りたくなったので、infoseekで調べてみる。すると、いわき明星大学の清水・榊原研究室の「粘弾性動モデル」が引っ掛かる。
参考:
衝撃吸収・シリコーンの弾性率などに興味を持っている人には面白いかもしれない。もう少し調べてみると「バナッハ空間バナッハスケールにおける分数階積分作用素」というようなキーワードも引っ掛かる。
そこで、まずは勝手に分数階微分について考えてみた。
分数階微分・積分の勝手な想像図
まずは、イメージを考えるためにグラフを作成してみる。x^2の関数、および、それを微分・積分した関数である。微分は3階まで、積分は2階まで行っている。
 |
このグラフ形式の表示をちょっとだけ変えてみる。
 |
ここまでくると、平面グラフにしてみたくなる。つまり、微分・積分の階数を離散的な整数値でなく、連続的な値としてのイメージに変えたくなる。
 |
これで、微分・積分が整数階でない場合のイメージ(勝手な)ができた。微分・積分が離散的なものではなくスムーズにつながっているものであるというイメージである。図.2から図.3への変化をよく覚えていてほしい。
といっても、これは数学的なイメージのみで物理的なイメージはまだここでは持っていない。位置、速度、加速度などの微分・積分で選られるものに対して同じようなイメージを適用すると、位置なんだけれどちょっと加速度っぽいもの、とか、速度と加速度の「合いの子」みたいなものというような感じだろうか?
さらに、これから先は、f(x)という関数が示す無限個の値を位置ベクトルと考えて、f(x)というのは無限次元空間の一つの点だというイメージを持つことにする。線形代数を考えるならそれが一番わかりやすいだろう。任意の階で微分された関数群が集まって、さらに高次元の空間をなしているというイメージである。
分数階微分を調べる
勝手なイメージはここまでにして、手元にある数学の参考書の中から手がかりを探してみた。すると、大学院入試問題解説 - 理学・工学への数学の応用 - 梶原壌二 現代数学社ISBN4-7687-0190-6
の中に手がかりがあった。あれ、ということは以前にやったはずなのか...そう言えばおぼろげな記憶がちょっと...
その中の言葉を少し引くと、
フーリエ変換は等距離作用素である、関数空間L^2(R)における回転といえる。結局、
となる。そして、古典力学におけるハミルトン関数において、運動量を微分演算子で置き換えれば、量子力学や量子化学のハミルトン演算子が得られ、シュレディンガー方程式などにつながるのである、とある。他の資料を眺めてみると、どうやら量子力学などの分野からの要請に応じてここらへんの微分演算子の分野が発展しているようだ。理論物理などをやった方ならよくご存知のことだろう。例えば、水素原子の基底状態の波動関数へ運動エネルギーの演算子を作用させるというような、基本的な所でも、このフーリエ変換を用いた微分演算が用いられてる。ここで、fは元の関数であり、Fはフーリエ変換
さて、この式自体は非常に簡単である。それにイメージも湧きやすい。
i を掛ける演算、私のイメージでは複素数空間の中で90度回転をする(言い換えれば、位相が90度ずれる)演算、が微分・積分であるというイメージはスムーズに受け入れやすい(それが正しいかどうかは知らないが)。なぜなら、微分が空間の中での回転であるとすると、三角関数の微分・積分に関する性質(例えば、Sinを微分するとCosに、Sinを2階微分すると-Sinになる、すなわち、一回の微分につき位相が90°ずつ回転する(位相がずれる)というような性質)が納得でき、それがフーリエ変換という形で登場してくることがスムーズに受け入れられるのである。また、微分といえばとりあえず三角関数の登場というイメージもある。
もう少しわかりやすく書くと、
- 三角関数では一階微分の結果は90度位相がずれる(回転する)。
- ならば、(例えば)0.5階微分は45度位相をずらせば良い。
- 任意の関数もフーリエ変換により、三角関数に分解される。
- ならば、任意の関数に任意の実数値の微分が成立する。
任意の関数をフーリエ変換し三角関数に分解した時の位相、言い換えれば、周波数領域での位相ずらし、で分数階微分が定義されるということは、物理的実用的に大きな意味を持つ。例えば、電磁波、弾塑性運動などの物理現象の中での位相変化を分数階微分で解けることになる。例えば、複素貯蔵弾性率などについて分数階微分との関係は深そうである。あるいは、媒体中の電磁波の位相などについて適用するのも面白そうである。
分数階微分を使ってみる
よく分からないところも多いが、とりあえず、
という式を使ってみる。まずは、使ってみないとわからない。とりあえず、1次元の関数を作成して、この式を適用してみる。まずは、よく出てくるガウス分布で適用してみる。まずはガウス分布とそれの通常の一階微分の解析解を求める。
 |  |
それでは、今回の方法による一階微分の結果と、それと解析解との比較を示す。なお、本来無限領域のフーリエ変換を有限の領域で行っているため、端部近くで変なことが生じるのはしかたがないだろう。また、色々な事情により係数の違いは無視して欲しい。
 |  |
ちょっとずれが生じているが、こんなものだろう。しかし、これだけでは今回のフーリエ変換を用いた微分の面白さはでてこないので、0から2の範囲で連続的に分数階微分をしてみる。
 1/10 (=0.1)階微分 |  1/2 (=0.5)階微分 |  7/10 (=0.7)階微分 |  1階微分 |
 13/10 (=1.3)階微分 |  15/10 (=1.5)階微分 |  17/10 (=1.7)階微分 |  2階微分 |
モーフィングのようで面白い。
さて、今回は分数階微分を勉強してみる所までで、これの応用は別に行ってみたい。もちろん、言うまでもないと思うが、間違いは多々あると思う。いや、田舎に住んでいるもので資料がないんですよ。
1999-09-20[n年前へ]
■深夜特急 '99 
HIRAX発ロンドン行きWEBの旅
新しい情報を探しに
お笑いパソコン日誌 (http://www2s.biglobe.ne.jp/~chic/pilot.html )を見に行くと面白い情報があった。それは、
Webの分離度合いは19クリック分?である。
( http://www.zdnet.co.jp/news/9909/10/www.html)
内容のポイントは
- 「Nature誌の9月9日発行号の掲載された2つの研究が明らかにしているように,WorldWide Webは急速に,1つの有機生命体としての進化を遂げつつある。Webの成長のダイナミクスとトポロジは,物理学の世界のPowerLawとして知られている法則に従っている」
- 「ネットワーク内の2点間の平均最短経路,つまり“直径”を求めることができる。Web上に8億のドキュメントがあるという推定が正しいとすれば,無作為に抽出した2点間の平均“距離”は19リンクになる。」
そうであるならば、ぐずぐずしてはいられない。もちろん、WWW.HIRAX.NETをスタート地点として、WEBの旅を続け、ロンドン中央郵便局を目指すのだ。平均“距離”が19リンクなら案外と近いかもしれない。WEB上で19回位のヒッチハイクをすれば良いことだ。そして、旅の最終地点であるロンドン中央郵便局からメールを出すのだ。「ワレトウチャクセリ」、と。(何のことか判らない人は沢木耕太郎の「深夜特急」を読むべし。)
そう決めた私はビールを片手にユーラシア大陸横断の旅に出かけた。さぁ、右手の親指を突き出し、ヒッチハイクのポーズで(Libretto50だから)、WEBの旅のスタートだ。
0 http://www.hirax.net/もちろん、旅のスタート地点であるwww.hirax.netだ。ここのTopページからの数少ないリンクサイトからLaboFinderへ飛ぶ。1 LaboFinder http://www.labofinder.org/まずは、Linkページへ飛ぶ。2 http://www.labofinder.org/links/links_index.html会員のWEBへのLinkページへ行く。3 http://www.labofinder.org/links/links_member_index.htmlここから、でわとしかずさんの「ある化学者の屋根裏部屋」へ行こう。4 http://www.asahi-net.or.jp/~av4t-dw/index.html次は、化学系サイトへのリンクへ。5 http://www.asahi-net.or.jp/~av4t-dw/link2chem.htmlそして、University of Leeds (United Kingdom)だ。6 http://chem.leeds.ac.uk/default.htmlここのTravel Informationを選ぶ。7 http://www.chem.leeds.ac.uk/Travel.htmlBritish Airwaysへ行く。8 http://www.british-airways.com/もちろん、Traveller's Guide to Londonだ。9 http://www.british-airways.com/london/Resourcesを選んで、10 http://www.british-airways.com/london/resource/resource.shtmlLondon on the Webへ行く。11 http://www.british-airways.com/london/resource/links/links.shtmlThe London Tourist Boardへ行って、12 http://www.londontown.com/Mapsを選ぶ。13 http://www.londontown.com/maps/St.James Parkへ行って、14 http://www.londontown.com/maps/index3.phtml?grid=H7右へ一回移動して、15 http://www.londontown.com/maps/index3.phtml?grid=J7&letter=&street=&titlegif=こんどは上へ移動する。16 http://www.londontown.com/maps/index3.phtml?grid=J6&letter=&street=&titlegif=
さぁ、Trafalger Squareに到着だ。この横にロンドン中央郵便局はあるはずだ。
やっと、Trafalger Squareの近くのロンドン中央郵便局に辿りついた。えっ、単なる画像じゃないかって?まぁいいじゃないの。ここまで、結構時間がかかっているんだから...何しろユーラシア大陸を横断したんだから。それに真っ直ぐ辿りついたわけじゃないし...
それに16回のクリックで辿りついたのだから、最初の19回という予想にも結構近い。
 |
トラファルガー広場をしばらく眺めた後、NotePCを抱えた私は郵便局員に聞いた(心の中で)。
「電子メールを出したいのですが?」すると、彼女(私の想像の中の郵便局員はもちろん女性だったのだ)は
「電子メールを出すのは郵便局からではありません。」と言った(心の中で)。
言われてみれば(心の中で)、電子メールは郵便局で出すのではなかったのだ。別にどこからでも出せるのだった。別にイギリスまで来る必要もなかったのだ。それならば、例えどこであっても私が決めればそこが旅の終点と決めた「ロンドン中央郵便局」だ。旅の終点の「ロンドン中央郵便局」の場所は私が決めれば良いことだったのだ。
何しろ、プロデューサーにゴールを決められているわけじゃないしね。
1999-10-18[n年前へ]
■沸点と数学の挑戦状 
みつからない「解決編」
| いったい、いつから疑問に思うことをやめてしまったのでしょうか? いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか? いつだって、どこでだって、謎はすぐ近くにあったのです。 何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。 加納朋子 ななつのこ より |
加納朋子の「ななつのこ」という小説を読んだ。創元推理文庫から出ているのだから、ミステリといっても良いだろう。私の好きな北村薫の「空飛ぶ馬」に始まる「円紫さんと私」シリーズによく似た雰囲気を持つ本である。
それを読んで、ふと思い出した。
私が通っていたM高校の話だ。M高校は武蔵野の玉川上水のほとりにある。
そのことを聞いたのは月曜の朝だ。日曜日の昼間に変質者が現れたというのである。目撃した人によれば、変質者は生徒用の上履きを履いていて、手には白い布を持っていたという。顔などはよくわからなかったそうだ。目撃者に驚いた変質者は逃げてしまい、白い布を落としていった、というのだ。
それだけなら、「単なる変な奴がいた」ということで話は終わった筈だ。問題は、その白い布に麻酔薬が含ませてあったという点だった。悪ふざけではすまない。
私は友人の鴨志田とその事件について話をしていた。気になることがあったからだ。変質者が目撃された場所が問題だったのだ。図に描くとこんな感じだ。
 |
 |
そこは2階の中では職員室から一番遠い。一番校門に近い玄関を揚がった所である。そして、生物室の隣だった。
生物室は、普通の教室とは違う。通常は鍵がかかっているし、それは鍵がかけられるということでもある。
生物部の部長・副部長は生物室の鍵を使える立場にあった。そして、鴨志田は生物部の部長だった。
「変質者は生物室に出入りできる奴かな?」これはどうにも重大な問題だったのである。
「生物の部長・副部長経験者ってこと?」
「うーん。」
「麻酔薬ってクロロホルムとか、かな?」と鴨志田にぼくが言うと、「立て板に水」状態で、彼の推論を聞かせてくれた。
「いや、きっとエーテルだね。」なるほど説得力はある。いや、ありすぎるといっても良い程だ。コイツ、むちゃくちゃ怪しいヤツである。犯人候補No.1である。一朝一夕で考えた理屈とは思えない。
「今時、クロロホルムなんて使われていないんだよ。」
「副作用もあるしさ。」
「あと、沸点を考えてみろよ。」
「エーテル、つまりジエチルエーテルDiethyl Ether ( (C2H5)2O )は沸点が34.6℃だ。」
「それに対して、クロロホルムChloroform ( CHCl3 )は沸点が61.7℃だ。」
「ハンカチにクロロホルムを含ませて顔に当ててもなにもおきない。」
「だけど、エーテルは人間の顔にあてたら、体温のせいで瞬間的に気化するんだよ。」
「つまり、エーテルの気体で顔の周りが覆われるわけだ。」
「呼吸なんかしたらエーテルを吸わざるをえないだろ。」
「だから、クロロホルムとかよりエーテルのほうが、変な用途には向いているんじゃないかな。」
「もっとも、即座に気を失うとは思えないけどね。」
「そういうことって生物部の部員ならみんなわかるもの?」と聞くと、
「部長・副部長をやるくらいの人は確実にわかる。けど、他の人でもわかるやつはきっと多いよ。」また、部長・副部長経験者である。
「ところで、生物室にエーテルはある?」と訊くと、
「うん、あるよ。」とのお答え。やはり、生物室の「鍵」である。
「生物室に入れる人なら手に入ると思うよ。」
「せめて靴の先の色がわかれば。」そう靴の先の色は赤・黄・緑と色分けされており、それで1,2,3年生の区別がつくのだ。もっとも、それと関係ないサンダルを履いている人のほうが実際は多いのであるが。それに、靴を履いていたから学内の生徒とは限らないが。
「学年がわかるね。」
次に、ぼくらは覚えたばかりの数学の知識をひけらかす(まだ高校生だから)話をしていた。
犯人(変質者)の条件
- 男
- 生徒用の上履きを履いてた。
- 麻酔薬に関する知識がある。
- 麻酔薬を手に入れられる。
- 生物室に入れる。
- 一人
ここで、私は
「ぼくは生物室の鍵を持っていないから、必要条件を満たしていないな。」
つまり、「生物室に入れる=鍵を使える=生物の部長・副部長経験者」であるから、「ぼくは必要条件のひとつを満たしていない」と主張したのだが、鴨志田は聞き入れなかった。。
「オマエに鍵なんか必要ないだろう。」
そう、物理部の部長(私のこと)になるには「錠前破りが得意」でなければならなかったのである。すなわち、物理部の部長経験者であると「生物室に入れる。」ということの「十分条件」をもれなく手にしてしまうのである。イヤーなおまけである。もっとも、私は生物・化学は苦手であるので、必要条件を満たしていない。
一方犯人の「十分条件」を考えてみるとこんなものがある。
- 生物部の部長・副部長
 |
「ところで、こんなミステリがあったらどう思う? 探偵がめちゃくちゃ論理的なヤツでさ。」さてさて、普通ならばここに「読者への挑戦状」が入るところだろう。だから、この話にも入れてみる。ただ、少し定型とは違う。
「コンパクト群の表現論なんかで語られてさ。」
「犯人を指摘する所なんか、数式だらけな話。」
「作家はMathematicaをワープロ代わりにしててさ。」
「......なんか、一般受けしそうにないな...おれにすら面白くないぞ...」
| ここまでに、犯人を示す証拠が全ての証拠がそろっているとは思わないし、そもそも、犯人が登場しているかどうかすら私にはわからない。いや、実際のところ登場していないと100%確信している。しかし、名探偵のあなたなら、きっと犯人を指摘してくれるに違いない。私と鴨志田の懸念を吹き飛ばしてくれるに違いない、と思うのだ。 犯人は一体誰なのだ... |
1999-12-12[n年前へ]
■色覚モドキソフトを作る(色弱と色空間その4) 
五十歩百歩
まず、先に書いておこう。今回は、
で作成したTrueColorと似たようなプログラムを作成してみたい。何しろ関係ない話が以降、長々と続くからである。昔から、科学者は「色」というキーワードに強く惹かれている、と思う。そんなことを私が思うまでもなく、量子色力学(quatumchromodynamics)、色つき空間群(Color-symmetry)等のキーワードにその事実は現れている。これらの言葉は普通に使われる「色」という言葉とは違う性質を表すものである。しかし、科学者が「色」というものを基本的なものであると感じているために、どんなものが対象でも、「性質」の代表的なものとして、「色」という言葉が連想されるのだろう。
私は学生時代の量子力学の授業のおかげで、「色」という言葉を聞くと今でも眠くなってしまうのである。何しろ、私の通う理学部の教室の横は農学部の畑だったのだ。教授の声と共に「モゥーーー」という牛の鳴き声が聞こえてくるのだ。教授の声と牛の鳴き声が絶妙のハーモニーとなるのである。ただでさえ眠くなるのに、そのハーモニーはクロロホルムもビックリの睡眠作用を発揮するのだ。私はそのハーモニーのおかげで何回も記憶を飛ばされた。
また、その牛達のおかげで、授業の中で「匂い」と聞いたりすると、牛の糞の「匂い」しか連想できないのである。困ったものである。あの農学部の畑がなければ、もしかしたら私は量子力学を好きになっていたかもしれない。そして、量子力学を極めていたかもしれないのだ...簡単に言えば私は量子力学の授業では落ちこぼれてしまったわけだ。
ところで、昔の科学者達を考えると、「色」に関わらなかった人を探すほうが逆に難しいように思う。ニュートン、マクスウェル、ヤング、ヘルムホルツなどが代表的である。当たり前である。物理・化学に関わらず、「光」には関わらざるを得ない。当たり前である。さまざまな計測を行ったり、エネルギーを考えたりする上で光は最も重要なモノである。
そして、「色」というものは「光」の大きな性質の一つである。しかも、それは「科学者自身にとっても」目に見える性質である。目に見えるものを無視する科学者は少ないと思われるので、科学者が「色」に関わらないわけにはいかないのだ。
割に最近の科学者でも、意外な分野の人が「色そのもの」の研究をしていることがある。例えば、シュレディンガーなども色空間の提唱をしていたらしい。確かに、量子力学から色空間へはつながりを感じないこともないのではあるが、少し意外でもある。そのシュレディンガーが提唱した色空間がどのようなものであるのか、私は残念ながら知らないのだが、波動を深く研究していたシュレディンガーが提唱する色空間というのは非常に興味のあるところである。また、化学。物理学者であるダルトンは自らも色弱であるため、特にその辺りのことを研究し、報告している。
さて、そのダルトンをinfoseekで検索してみると、
- ダルトンレンズ (http://www2u.biglobe.ne.jp/~ohsaka/index2.html )
もちろん、WEBページは会社の心(色弱と色空間 その2) - WEBページのカラーを考える 3 - (1999.08.10)で作成したTrueColorも同じような目的のために作成したものであるが、あれはあまりにも大雑把なモノだったので、作り直してみたいのである。なお、今回は画像のRGBとL、M、S錐体の反応の間の変換は
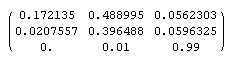 |  |
そこで、こういったWEB上の画像を読み込んで、
でやったL,M,Sの各錐体の感度が低いときの色覚シミュレーションを行うソフトを作成してみた。ソフトはこれである。前回と同じく、Susieプラグインを用いて画像を読み込んでいるので、「Susieの部屋」などから、Susie本体・あるいはプラグインを入手する必要がある。また、手間を惜しんだためProxy対応にはしていない。さて、動作画面サンプルを以下に示す。初期状態では
- ダルトンレンズ (http://www2u.biglobe.ne.jp/~ohsaka/index2.html )
 |
この画面例では各錐体の感度は全て100%になっている。
それでは、以下に適当に錐体の感度パラメータを変化させた場合のサンプルを示してみる。
 |  |
こうしてみると、これまで見てきたものとは違う数字が浮かび上がることがわかる。89,52などである。こういう仕組みを用いたのが、石原式などの色覚検査のやり方である。つまりは、異なる色を識別できないこと、すなわち、混同色を用いているのである。混同色を用いて文字を描くことにより、色弱であるかどうかを判断しようとするものだ。
さて、こういった書き方をすると、色を混同してしまうのが色弱の人だけと勘違いされてしまいそうであるが、そんなことはない。全ての人が「色を混同してしまう」のである。どんな人でも、異なる波長の光であっても、例えばRGBなどの(多くても)三色を混合すれば同じ色に見えてしまう。つまりは、混同色だらけなのである。健常者と呼ばれるヒトも色弱と呼ばれるヒトもたかだか数種類の錐体を持つにすぎない。
色々な光の波長分布を認識できる生物がいたとすると、彼らがからすればヒトは全て色弱ということになるのだろう。つまりは、五十歩百歩といったところなのかな、と思うのである。
1999-12-19[n年前へ]
■母に捧げるバラード 
宿題は自分でやってくれぇ
今回の話は、とあるメーリングリストから始まる。仮にそのメーリングリストを"family-ml"と名付けておく。そのfamily-mlで論争が起きたのである。
メーリングリストで論争が起きることはよくある。しかし、このfamily-mlは通常のメーリングリストではなかった。実は、とある家族を構成員とするものであった。そう、この家族は専用のメーリングリストを持っているのである。そこで、この論争は起きた。
各登場人物の紹介は随時していこうと思う。
| To family-**@hirax.net From 母 Subject: レポート課題がわからない みなさんお元気ですね。 大気の持つ質量あたりのエネルギーを、次の二つの例について求めなさい。 「下」 赤道付近の地表面付近の大気 「上」 赤道付近り対流圏界面付近の大気 結果を次のような表にまとめなさい。 さて、インドの話はいらしたときにします。大変な国ですが、行って良かったです。 母 |
この「母」はいまはやりのヤンママではない。戦中に生まれたお年の方である。去年辺りから仕事のない日に大学へ社会人学生として通うようになったのである。
| To family-**@hirax.net From 兄 Subject:Re: レポート課題がわからない > レポート課題 SOSです。だれか教えて下さい。 この「母」のレポートって「弟」の得意な専門の問題じゃないの? > 高さ 1500m(=15Km) あと、15000mの間違い? 兄 |
「兄」はとあるWEBのwebmasterである。「母」の年からすれば、そうそう若くもないことがわかる。
| To family-**@hirax.net From 父 Subject:Re: レポート課題がわからない >結果を次のような表にまとめなさい。 父 |
「父」はhiraxという名前を数十年名乗ってきた、元祖hiraxである。
| To family-**@hirax.net From 母 Subject:Re: レポート課題がわからない 今年は地球科学概論をとった。確か昨年「兄」が次は地球科学がいいと、 母 |
確か、この「母」は去年は「応用化学」をとっていた。なぜ、そういう無理なことをしたがるのだ。
気持ちはわからないでもないが、もう少し考えて欲しいものである。
| To family-**@hirax.net From 兄 Subject:Re: レポート課題がわからない > 今年は地球科学概論をとった。確か昨年「兄」が次は地球科学がいいと、 いや、私が言ったのは「どうせ習うなら自然科学史みたいなのの方がいいよ。」です。「地球科学概論」だなんて言っておりません。 >自分の責任のあることを「弟」に振ろうとしていませんか。 いや、私に責任はないと思うのですが... >だれでもいいです。「弟」、助けてくれますか? そうそう > 「弟」 兄 |
| To family-**@hirax.net From 弟 Subject:Re: レポート課題がわからない >そうそう > 「弟」 地球科学概論なんだから、宇宙・地球物理専攻の人がやるべき 最近、修論のまとめで忙しいです。 弟 |
| To family-**@hirax.net From 兄 Subject:Re: レポート課題がわからない > 地球科学概論なんだから、宇宙・地球物理専攻の人がやるべき しかし、これってほとんど化学工学ではないでしょうか。だから、 兄 |
| To family-**@hirax.net From 母 Subject:Re: レポート課題がわからない >>> そうそう助けてやれよ > 「弟」 そろいもそろって、冷たい兄弟ですね。 母 |
うちの「母」はこうなると怖い。
| To family-**@hirax.net From 「妹姉」 Subject:Re: レポート課題がわからない >>>> そうそう助けてやれよ > 「弟」 >そろいもそろって、冷たい兄弟ですね。 そういうと、私まで一緒みたいに聞こえます。やめて下さい。兄妹とか姉弟 「妹姉」 |
| To family-**@hirax.net From 父 Subject:Re: レポート課題がわからない 「母」がせっかく苦労してレポートをと考えているので、hiraxファミリーの 多分、「兄」や「弟」だったら、チョチョイだから。 > どうせ習うなら自然科学史みたいなものの方がいいよ。 父 |
| To family-**@hirax.net From 兄 Subject:Re: レポート課題がわからない >多分、「兄」や「弟」だったら、チョチョイだから。 >今朝、「父」は物理的な意味だけは、10分間講義してあげました。 そんなに若くはない年で働きながらも、大学へ行こうとする「母」の 兄 |
さて、配達された最後の手紙が以下である。
| To family-**@hirax.net From 兄 Subject:Re: レポート課題がわからない 昨日の電話など、何やらプレッシャーが感じられてきたので、適当に問題にとりかかって まずは、簡単そうな位置エネルギーと運動エネルギーから。「地球科学概論」 「問題」 「上」 赤道付近り対流圏界面付近の大気 「上」「下」それぞれについて 「回答」 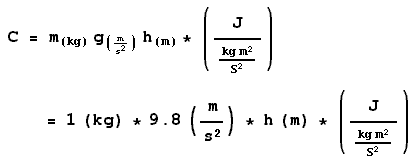 「上」 赤道付近り対流圏界面付近の大気 h=15000(m) 「下」 赤道付近の地表面付近の大気 h=0(m) を代入し、 「上」 1.47*10^(5) J 「下」 0 J を得る。 運動エネルギーDは速度v(m/s)に対して、 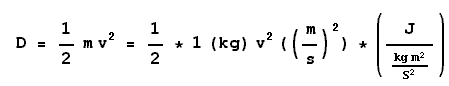 「上」 赤道付近り対流圏界面付近の大気 v=20(m/s) 「下」 赤道付近の地表面付近の大気 v=5(m/s) を代入し、 「上」 200 J 「下」 12.5 J を得る。 さて、次に「A.内部エネルギーの温度に比例する部分、B.内部エネルギーの水蒸気に比例する部分」 「上」 赤道付近り対流圏界面付近の大気 (300-6×15)K 最後に「B.内部エネルギーの水蒸気に比例する部分」であるが、水が液体から気体に変化するときのエネルギー収支を考る。蒸発熱が2498J/gであることを考え、計算を行う。 「上」 赤道付近り対流圏界面付近の大気 水蒸気0g なお、検算も読み直しもしておりません。 兄 |
ごくまれにではあるが、「課題を解いてください」という大学生からのメールが届くことがある。そういうメールを見るたびに「うーむ...」という気分になっていたのである。しかし、まさか自分の親の宿題をやるはめになるとは。しかもこの年になって...