hirax.net::Keywords::「面積」のブログ

■OHPによるモアレと光の干渉の相似について考える。　　

ヒラックス・ディザの提案

「位相保存ディザマトリックス」

4x1ドットからなるマトリックス

　この「黒、黒、白、白」というパターンを次の図と見比べる。

位相遅れ0の矩形波、(4つに分割すると、「黒、黒、白、白」となる)

4x1ドットのマトリックスで各位相の矩形波を表現した例1

「モアレのデバイス依存について考える。」で行ったようにこのようなパターンをOHPで打ち出し、重ね合わせてみる。例えば、位相0と位相180のものを重ね合わせたらどうなるだろうか。4x1ドットのマトリックスの全てが黒になる。すなわち、真っ黒になるのがわかるだろう。それでは、位相0と位相90のものではどうだろうか。4x1ドットのマトリックスの内、3ドットが黒、1ドットが白である。位相が同じものどうしを重ね合わせると、元と同じく、2ドットが黒、2ドットが白である。
　ということは、「位相が同じ物どうしであれば、元の明るさを保持する」、「位相が逆であれば真っ黒になる」、「位相が少しずれているのあれば、明るさはその分少し暗くなる」という性質があることがわかる。光の干渉の場合とほとんど同じ性質を持っているのがわかると思う。違うのは、同じ位相のものどうしが重ね合わさった時に、重ね合わせた分明るさが2倍になるか、そうでなくてそのままなのかという違いだけである。
　つまり、この4x1ドットのマトリックスは「きちんと演算が成立する位相情報が記録されている」ということになる。そして、位相が異なるものを重ね合わせた時の位相情報の保存までも考えてやるならば、先ほどの例1は次のように位相の定義を変えてやるほうがいいと思う。

各矩形波の黒の中心位置として位相の値を定義し、4x1ドットのマトリックスで各位相の矩形波を表現した例2

　この例2では位相の数字は各矩形波の中心位置を現すことにしている。それでは、この定義を用いて、位相90,180のものを足しあわせたらどうなるだろうか。下に示すのがその結果である。

例2の定義を用いて位相90,180を足しあわせると

　位相90と位相180のものを足しあわせると、波形はブロードになり、中心すなわち位相135のものができているのがわかる。また、明るさはこれまでが、2/4だったものが1/4であることになり、強度も弱まっているのが表現されている。

　つまり、このようなマトリックスによる表現は波の持つ位相と強度と波形を表現し、演算も成り立っていることがわかる。それでは、例2の基本マトリックスが縦方向に繰り返されている画像(1(基本マトリックス)x8ピクセル)を考える。こんな感じである。

例2が繰り返されているもの

　これは下方向から進行している矩形波の様子そのままである。なお、この図でも基本となるマトリックスは4x1ドットであるから、この例では要素としては1x8ピクセルを示しているのである。どの要素も振幅(強度)自体は同じである。平均の明るさは同じである、と言い換えても良い。また、波形自体も同じである。しかし、位相が異なっている。波の進行そのままである。

さらに強度情報を加える

4x4ドットのマトリックスで強度の快調を表現した例A

4x4ドットのマトリックスで強度の階調を表現した例B

　このような「位相、波形、強度情報を保存し、演算も成立する」マトリックス表現を仮に「HiraxDither(ヒラックス・ディザ)」と呼ぼう。先の「モアレのデバイス依存について考える。」で使ったスペックルパターンの例はこのヒラックス・ディザの簡易なもの(2x1基本マトリックスのもの)を使っていた。
　また、「モアレのデバイス依存について考える。」で使った同心円状の画像のモアレのパターンは実はヒラックスパターンの特殊な例(1x1基本マトリックスのもの)を用いていたのである。そこでは、単に位相情報しか記憶されていない。この場合には、白、黒が位相情報を現していたのである。だから、黒、黒どうしの所(すなわち、位相が同じ所)では平均の明るさは変化せず、黒、白が重なった部分(すなわち、位相が反対である所)でのみ打ち消し合い、暗くなっていたわけである。波形も、強度情報もこの場合には記録されていない。

「ヒラックス・ディザ」とホログラフィーの相似点

　また、もう少し深く考えると、もっと他の分野とも繋がるかもしれない。いずれ、また考えてみたい。

■電界計算をしてみたい[有限要素法編その1]　

有限と微小のパン

　今回のサブタイトルは一目瞭然であるが、森博嗣のミステリのタイトルそのままである。

森博嗣 著 「有限と微小のパン」

　何故、「電界計算をしてみたい-有限要素法編その1-」が「有限と微小のパン」に繋がるのか。もちろん、"有限要素法"と"有限と微小のパン"の「有限」をかけた駄洒落ではない。有限要素法を考えるとき、私は森博嗣に足を向けては寝ることができない。それが、なぜかは下の本を見ればわかる。

森博嗣 著 「C言語による有限要素法入門」

　これは、学生時代に有限要素法を勉強するために使った本である。「森 博嗣　著」と書いてあるのがわかるだろうか。いや、まさかこの本の作者がミステリを量産するとは想像もしなかった。ビックリである。講談社ノベルズと森北出版の両方から本を出している人は他にはいそうにない。

　本題と関係のない話はここまでにしておく。今回はMathematicaで有限要素法を用いて静電界計算を行いたい。とりあえず、ソルバーとプリ・プロセッサまでつくる。その応用は続きの回で行いたい。Mathematicaで有限要素法を勉強するには、森北出版の依田　潔　著「Mathematicaによる電磁界シミュレーション入門」を参考にした。任意の電荷配置のPoisson方程式を解くようにしてある。

　今回使用したMathematicaのNotebookをHTMLで出力したものをここに示す。Notebook中でエラーが表示されているところは初期設定の変数をきちんと設定してやれば、エラーは出ないはずである。

次回に詳しく計算モデルの説明を行うので、今回は計算モデルの詳細については記述しない。Notebook内に、モデルの詳細は記述してある。

　このNotebookを使った計算、出力例を以下に示す。

電界計算の例

平行平板電極の間に誘電体層があるモデル	平板電極と三角柱電極の間に誘電体層があるモデル	平板電極と円柱電極の間に誘電体層があるモデル
分割要素	分割要素	分割要素
電位表示(色がきちんとしたhueでないことに注意)	電位表示(色がきちんとしたhueでないことに注意)	電位表示(色がきちんとしたhueでないことに注意)
半分の領域の電位を鳥瞰図にしたもの	半分の領域の電位を鳥瞰図にしたもの	半分の領域の電位を鳥瞰図にしたもの

　Mathematica3.0のHTML出力は大変便利だが、漢字が化けるのが困りものだ。しかも、ちょっと似た漢字に化けてしまうからわかりにくい。今回のNotebook中で化けた漢字を以下に示す。

• 油界　<- 電界
• 堰素　<- 要素
• 誘油　<- 誘電
• 姦み込む　<- 組み込む
• 表傭　<- 表面
• 壓さ　<- 高さ
• 堆心　<- 重心
• 肖似　<- 近似
• 内占　<- 内部
• 傭積　<- 面積
• 回寂　<- 回転
• 進当　<- 適当
• 懷瞰　<- 鳥瞰

中国語みたいな化け方である。しかも、意味としても何か変な化け方である。いつか、この対処方法と理由を考えてみたい。それにしても、週末の遊び道具としてはMathematicaは素晴らしいと思う。

■不思議な品揃え　

パンティーププラザの未来

　下の写真はバンコクのパンティーププラザの内部である。丸井のビルの内部をラジオ会館の店子で置換しまくったようなビルである。いや、ラジオデパートのスケールを長さで10倍、面積で100倍にしたといった方がいいだろうか。

パンティーププラザの内部

　こういった電脳ビルに関しては詳しいサイトがたくさんあるのでここでは言及しない。

　私が興味を惹かれたのは、その品揃えの不思議さである。パンティーププラザ内には数多くの店がある。どの店も展示しているソフトウェアは技術者向けのソフトのコーナーがかなり広いのである。それが結構面白いのだ。展示しているソフトウェア自体はどこの店も対して変わらない。例えば、

• AVS/Express Developer
• ＭＡＴＬＡＢ5.3
• Mathematica4.0
• 様々なCAD/EM Simulator

　もちろん、他の国では海賊版のソフトウェアに対する規制が厳しいため、売り場が縮小するとともに、売れ線のソフトのみが残ったというようなこともあるのだろう。(あるいは、売れ線のソフトの面積を広くするのが面倒で、全てのソフトをただ並べているのだろうか?)
　香港などでは、数年前はFDベースという形で技術的なソフトウェアの在庫が結構あった。しかし、今では技術的なソフトウェアはほんの片隅に残るだけである。現在は、ほとんどがゲームかオフィス・グラフィックス用のソフトウェアである。FDベースだった理由はCDをプレスで作成してしまうと、少数しか売れない技術ソフトウェアは利益が出ないからである。

　ただし、最近の技術ソフトウェアはFDベースでなくてCD-Rベースのものが多い。FDよりもCD-Rの方が安いし、本物がCDベースだとCD-Rでないと駄目だろう。しかし、CD-Rベースのソフトウェアを400円程で売っていると、利益が出るのか心配になってしまう位だ。

　いずれにせよ、パンティーププラザにこんなに技術ソフトがおいてある理由はよくわからないし、その倫理性についても難しい問題だと思う。ただ、私が興味があるのはこいうソフトウェアを買うのはどんな客であるのか、だ。　別に、客の倫理性に興味があるわけではない。素晴らしい道具を簡単に入手できる世界の未来に興味があるのだ。それに一時期タイの人達と一緒に働いていた時期があるので、なおさら気にかかってしまうのかもしれない。ハンバーガーと同じ値段で、こういった素晴らしいソフトウェアが入手できるパンティーププラザの未来はどうなるのだろうか?(ソフトウェアを製作している立場の人からすれば、たまったものではないのだろうが。)

と、ここまでで終わるつもりだったが、何故か手元にこんな画像が有る。

ナゾのメニュー画面

1枚のCDにBeatlesの全曲(当然歌詞も)が入っているのである。こんなCDがあったらいいなぁ、と思っていたのだが、あるもんなんだなぁ。ここらへんの曲はもう年月を経て、権利も消失してる(はず)だからいいんだよなぁ。だから、買ってもいいんだよなぁ(別に買ったといってるわけではないけど...)。あれ、"Iwill"が聞こえてきたけど、これはきっと夢なんだ...

■ビックエッグの力学　

ドームを支える空気圧の謎

　この回は(トンデモ話)であり、中途半端であるのだが、反省を込めてこのままにしておく。直すのが、面倒くさいわけではないので、念の為。

　日本シリーズ'99をやっている(いた)。私は野球は特に好きでも嫌いでもないが、野球場でビールを飲むのは大好きだ。そういえば、今年はドーム決戦である(だった)。ドームといえば元祖「東京ドーム」だろう。「東京ドーム」のWEB

• 株式会社東京ドーム　(http://www.tokyo-dome.co.jp/about/index.htm )

　たった、0.3%の空気圧の差で400トンを支えるとは、ものスゴイ。すぐには納得できない数字である。別に疑い深い私でなくても不思議に思うことだろう。

　そこで、確かめてみることにした。まずは、東京ドームの面積をx(m) * x(m)としてみる。すると、持ち上げることのできる重さ(トン)は、

• 0.3 / 100(%から比へ) * 100(hPaからN/m^2へ) * x * x / 1000(kgからトンへ)* 9.8(Nから重力へ)

と計算できる(この式には実は間違いがある。詳細は後で...)。その結果を示してみる。

東京ドームのサイズに対する「持ち上げることのできる力」の計算結果
横軸=サイズ(m), 縦軸=「持ち上げることのできる力」(トン)

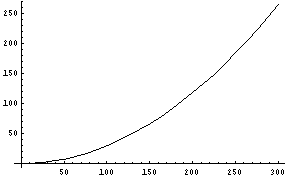　先の、Webから東京ドームのサイズを見てみると、x = 180mである。すると、持ち上げられる天井の重さは100トン程度であるということになる。おやおや、先の「400トンの天井を持ち上げる」というのとはずいぶん違う。これでは、天井を支えきれない。

東京ドームのサイズ

　そこで、高さによる大気圧の差を導入し、天井近くの高い場所では「外部の気圧が低い」という条件を導入してみる。0.3%というのは地上での比で、天井のある上空ではさらに差があるとしてみるのだ。うーん、強引である。

　さて、ここから後は(実は前も)トンデモ話になっているので眉に唾をつけて読んで欲しい。それを指摘して下さった、読者からの手紙への返事(とほぼ同じ内容)を下に示しておく。

青木さんへの手紙> 高さによる圧力の差は、高さの異なる二点間に存在する空気> の重さに見合ったものです。したがって、ドームの内部でも> 高いところほど圧力は低くなっている筈です。　その通りだと思います。WEB中で「うーん、強引である。」と書いたのはまさにその理由です。　それにも関わらず、強引な論法を続けたのは、文章の最後に「謎は解けないのに、東京ドームは存在している。 少し、くやしい。 」と書いた理由と同じです。まるで、「宇宙人が水道橋の駅前駐車場にUFOを停めて、サラ金に入って行くのを目の当たりにしている」ような、気持ちなのです。くやしいと強引になるのです。あぁ、何て人間らしいのでしょうか...　また、計算をしていた時に少し勘違いをしていました>もし、ドームの内外の温度が等しければ、地上でも天井でも内外の差圧は>同じになるはずです。と仰るとおり、差圧は等しいわけですが、それを0mにおける大気圧に対するパーセンテージに直すと、高度が高くなればなるほど、そこの気圧に対してはパーセンテージは高くなります。計算をしていた時にその「パーセンテージが高くなる」ことを「差圧が高くなる」ことと同じに扱うという間違いを犯してしまいました。もちろん、基準の気圧が小さくなっているので、パーセンテージが高くなっても本当は差圧は変わらないわけです。「考えることを手抜きしていた」と言ってもよいかもしれません。要反省です。>ドーム内の温度が高ければ空気の密度> が減少し、天井の位置での差圧はより大きくなり、天井を支> えるのに有利に働きます。これは、浮力によって天井が持ち> 上げられていると考えても同じ事です。> という訳で、ドーム内外の温度差が逆転する夏と冬とでは天> 井を支えるのに必要な圧力を変えなければならないと思うの> ですが本当はどうなんでしょうか。　これは面白そうですね。そういえば、学生時代に地殻物理学を専攻していたのですが、夏と冬の大気圧の違いから、地殻歪の大きさに関係づけて、地震の予言をするなら、「冬に発生する」といった方が良い、話(もちろんかなり冗談で)をしていた先生がいました。その先生に「今回のトンデモ話」がばれたら、大目玉をくらうこと間違いなしです。　ビックエッグの謎は深まるばかりです。それでは、また。------------------------------------------------------------------ch3coohさんへの手紙> > >12/(100*100)*1000= 1.2g/cm2となります。> > >> > >地上での大気圧は約1Kg/cm2なので、上の値は> > >1.2%程度となり、　ここが疑問だったのですが、これは1.2%でなくて、0.12%ですね。なるほど、0.3%よりも小さいですね。実に納得です。　さて、他の方からの指摘もあり、私の計算には> ＞0.3 / 100(%から比へ) * 100(hPaからN/m^2へ) * x * x > / 1000(kgからトンへ) * 9.8(Nから重力へ)> に１０１３（標準気圧 hPa）がかかっていないことが気になりました。　という間違いがあることがわかりました。全てはここが原因だったようです。　全ての疑問が解決しました。いやぁ、お恥ずかしい。また、他にも色々と面白い情報ありがとうございます。

　ひとつわかったことは、間違いをすると読者からの手紙が沢山来るといううれしくもつらい事実であった。ここから、あとは封印したい思いで一杯なのだが、自戒を込めてこのままにしておく。しつこいようだが、直すのが面倒なのではない。

　それでは、高さによる大気圧の差を計算してみる。理科年表から15℃の「標準大気の場合の高さと気圧の表」を見てみる。　ちなみに、東京ドームの温度は、「ガス熱源による冷暖房システムにより、夏期は28℃の冷房、冬期には18℃程度の暖房が行われている」とある。今回の計算は外気の温度が15℃で、内部は冬期には18℃程度の温度に調整されているものとしておこう。
　標準気圧は海抜0mで1013mbであり、200mでは989.5mbである。理科年表が古いのでPascal値でなく、mb表示になっている。

　これから、1m当たりのmb変化を計算すると、0.12mb/mとなる。比率に直すと、0.012%/mということになる。例えば、「ビルの1Fと9Fぐらい」の高さの差は30m位であろうから、それを大気圧の比に直すと、99.6%位となり、先の記述と大体合う。

以下に、高度に対する大気圧の差(の比 %)を示してみる。

高度に対する大気圧の比
横軸=高さ(m), 縦軸=大気圧の比(%)

　このグラフで30mの場所を見てみると、99.6%位というわけだ。これが、先のWEB上の「この気圧差0.3％は、ビルの1Fと9Fぐらいの違いがある。」という説明と合うわけである。

次に必要なのはドーム外部と内部の大気圧の比から、力に直してみる。基準面からの高さ0mにおける気圧を1hPaとして、1hPa = 10^2 N/m^2 = 10^2 m^-1 kg s^-2という単位換算を使うと、持ち上げることのできる重さは、

• (100-大気圧の差(の比 % )) / 100(%から単なる比へ) *9.8(重力に換算) / 1000(kgからトンへ)* 100(hPaからN/m^2へ) * x^2(ドームの面積)

　東京ドームの高さは「グラウンド面から　61.69m」とあるので大雑把に100mとしてみる。

天井の高さを100mとした時の、東京ドームのサイズに対する「持ち上げることのできる力」
横軸=東京ドームのサイズ(m), 縦軸=「持ち上げることのできる力」(トン)

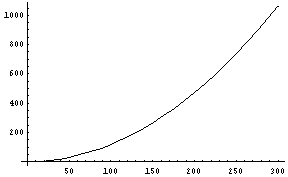　この計算結果によれば、東京ドームのサイズを180mとした時には、「持ち上げることのできる力」は400トン位になっている。ということは、先のWEBの記事と大体一致するわけである。

　しかし、この計算では致命的な欠陥がある。天井の高度が低いときには、400トンを持ち上げるためにはもっと高い「ドーム内部の圧力を必要とする」ことだ。

　例えば、0.3%空気圧の差の条件で、「天井の高度」に対する「持ち上げることのできる力」を計算してみると、次のようになる。

「東京ドームのサイズ」と「天井の高度」に対する「持ち上げることのできる力」
横軸=「天井の高度」(m), 縦軸=「持ち上げることのできる力」(トン)

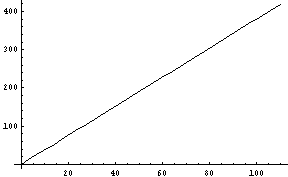　これでは、天井の高さが下がるとますます天井の重さを支えきれなくなってしまう。それに、そもそも天井をどうやって持ち上げたのだ?屋根を持ち上げるインフレートという作業はどうやって行ったのだろう?

　今回の計算は謎が増えただけかもしれない。謎は解けないのに、東京ドームは存在している。
　
　少し、くやしい。

■オッパイ星人の力学 第四回　

バスト曲線方程式 編

　そんなこんなでドキドキしながら封筒を開けると、記事のコピーが二つ入っていた。他には何も入っていないのである。一体これは何の記事だろう？と思いながらそのコピーを眺めてみた。すると、まずひとつは去年の12月25日付けの毎日新聞の科学欄である。二十一世紀を専門家達が予想した記事の横に「究める」というコーナーがあって、そこに「女性の胸と男性の好みの進化的関係は？」というインタビュー記事があった。そして、その記事が蛍光ペンでマーキングしてあったのである。

　これは一体、どういうことなのだ？と頭の中がグルグル＆複雑な気持ちになりながら、とりあえずその記事を読んでみた。すると、この記事がとても面白い。インタビュー中の

　ヒトは異性をどう選ぶのか？そんな疑問から女性のバストと弾性の好みに進化的関係があるかを研究している。

(中略)

　小さいバストほど魅力的だと母に教えられて育った。しかし、大きいバストが好きな男性がいることに気付いて驚き、「なぜ」と考えたのが研究のきっかけだった。

(中略)

　「大きいバストが本当に普遍的に好まれるかを知りたい。控えめなバストが淘汰されてしまうとは考えたくないから」と話す。

　そして、父からの封筒に入っていたもう一つの記事は宇宙科学研究所の新聞の中の宇宙基地利用研究センターの黒谷氏の「Anti-Gravity」というエッセイだった。なんでも、Anti-Gravityという化粧品があって、
それは顔の皮膚のコラーゲンに皮膚がたるまないようにするというものらしい。顔の皮膚にハリをあたえて、顔のたるみを防ぐのである。顔の皮膚のたるみ元をたどれば重力のせいだから、「anti-gravity= 無重力」化粧品ということになるわけだ。じゃぁ、このAnti-Gravityを体中に塗れば、バストやヒップが垂れるという女性の悩みもなくなるのではないか、と「無重力における生物の専門家」である黒谷氏は書いていて、参考文献に本サイトが挙げられていたのである。

　うむむ、世の中には巨乳の科学について進化論的に研究している人がいたり、オッパイの力学について考え（てみたりもす）る無重力生活の専門家もいるのだ。これはマズイ。油断している場合ではない。私もオッパイ星人研究をもっと真剣にしなければならない。父はきっと私に「研究の厳しさ」を教えようとしたに違いないのである。私の父はこれまでの「オッパイ星人の力学」を読んで、美味しんぼの海原雄山風に「うわあっはっ、こんなものでオッパイ星人の力学だとは笑止千万！」位のことを言ったに違いないのである。

　しかし、それだけではない。「二十一世紀、小さいバスト、大きいバスト、無重力、皮膚、オッパイのたれ」というヒントを与えてくれたのである。ここまでされて何かを書かなくて何としよう。オッパイ星人研究の手は一瞬たりとも休めてはならぬのである。そこで今回は「皮膚のハリ」や「重力」を気にしながら、「オッパイのたるみ・形状」について考えてみることにした。
 

　さて、一体バストの形状というものはどうなっているのだろう？これまでの「オッパイ星人の力学」では

• 半球モデル
• 円錐モデル

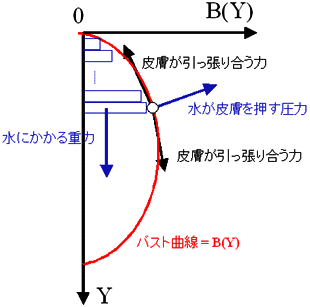
　というわけで、今回は新しいバストの形状モデルを提唱してみたい。それは「バストの内部は液体に満ちていて、その液体を外側の皮膚が支える」という

• 水風船バストモデル

　こんなモデルに基づいて、バストの形状を計算するにはどのように考えれば良いだろうか？次の図が「水風船バストモデル」における内部の水と各皮膚部分にかかる力を示してみたものである。これはバストの断面をを鉛直方向に示しており、左の黒い鉛直線が胸板であり、赤い線がバストの形状を示すバスト曲線である。（ちなみに、今回はバストを二次元の断面でのみ考えている。）
 

　「水風船バストモデル」における内部の水には重力がかかり、バストの下の方にいくほど圧力がかかっている。そして、皮膚に面している内部の水はその圧力を皮膚に伝える。そして、皮膚はその圧力で変形しながら水で満ちたバストを支えるのである。この時、バストの形状= 皮膚の形状を示すバスト曲線はどんな条件を満たしているだろうか？

　ここで、胸板にそって下向きにY軸をとり、バスト曲線をB(Y)で表すことにしよう。上の図をよく眺めるとわかると思うのだが、バストの形状= 皮膚の形状を示すバスト曲線をB(y)とすると、バスト曲線B(y)は実はこんな方程式を満たす。
 

「水風船バストモデル」におけるバスト曲線B(y)が満たす方程式

　まぁ、ここでは簡単のために、係数を省略していたり、バストが本当に垂れてしまうような状況は考えていなかったりするので、ごく簡易的なバスト曲線方程式だと思って欲しい。大雑把に係数などを無視して、言葉で言ってしまえば、バスト曲線の傾きの変化はその点より上に位置するバストの重量に等しい、という感じである。自由境界におけるLaplaceの関係でも連想して頂ければわかりやすいだろうか？とにかく、この条件と適当な境界条件さえ入れてやれば、「水風船バストモデル」におけるバスト曲線B(y)は計算することができるのである。
 

　さて、このバスト曲線方程式を一般化したり、係数をちゃんと計算したり、三次元に拡張したりということはまたいつか行うことにして、まずは適当にこのバスト曲線方程式を数値的に解いてみた。それが、例えば、次の図である。これが、「水風船バストモデル」のバストの形状の一例だ。
 

　この図の中でバスト形状のプロットが三種類あるのは「皮膚のハリ = 皮膚のヤング率」として三種類の値を使ってみたからだ。以前

• オッパイ星人の力学 - 胸のヤング率編- (2000.06.29)

　そう、もうお判りのはずだ。 「バストに関するヤング率」はまさにヤング率(Young率)なのである。実は年齢に比例する係数だったのだ

　さすがに、メチャクチャ皮膚のハリがある赤色のプロットなどは松坂大輔もビックリの「超ロケット乳」になってしまっているが（といっても、この図のアスペクト比に意味はないんだけど）、今や時代は二十一世紀、宇宙へロケットで飛び出す時代だと思えば、こんな「超ロケット乳」を眺めるのもそれまた一興ではないだろうか。ぜひこの「超ロケット乳」には宇宙へ飛び出してもらいたいものである。
 

　もちろん、世の中には「大きいことは良いことだ」という巨乳大好きオッパイ星人達もいるわけで、そんな人達のためにもう少し「大きいバスト」の場合で計算してみたものと並べて比較してみたのが次の図である。
 

「小さいバスト」と「大きいバスト」の計算結果

赤：すごくハリのあるヤングな皮膚の場合
マゼンダ：普通のハリを持つ皮膚の場合

藍色：ちょっとハリの少ない皮膚の場合

「小さいバスト」の場合

「大きいバスト」の場合

　個人の好みもあると思うが、けっこう自然な「巨乳形状」が再現できている。ちなみに、今回使用した簡易的なバスト曲線方程式ではすごく巨乳だったり、皮膚のハリが無さ過ぎてあまりにバストが垂れている場合の計算はできない。簡単に言えば、Yに対してバスト曲線B(Y)が一対一対応しないためである。が、それゆえに巨乳と言っても美乳の範囲のみ考えることができるのである。

　また、この「小さいバスト」の場合と「大きいバスト」の場合の比較から、「巨乳は垂れるのよっ！だから、小さい方が良いのっ！」という世の小振りなバストの女性がよく言うセリフの妥当性も確認してみたいところではなるが、そういうことは何か危険なことであるような気もしてきたので、今回は止めておきたい。

　ところで、今回の話はAnti-Gravityから話が始まっているわけだが、ちなみに「水風船バストモデル」は無重力下ではどのような形状をとるかと言えば、当然体積に対して表面積が最小となる「半球形状」になる。つまり、「半球バストモデル」は「水風船バストモデル」の重力を無視した特殊な場合であり、逆に言えば「水風船バストモデル」は「半球バストモデル」にバスト内部での重力の影響を加えて一般化したものだったのである。

　今回は、とりあえず新たに「水風船バストモデル」を提唱し、そのモデルにおけるバスト曲線B(y)を解くための簡易的な方程式を考察し、それを数値的に試しに解いてみた。次回は今回行った考察を用いながら、少し違うアプローチで「オッパイ星人の力学」を考えてみたいと思う。
 

　さて、今回の話のきっかけともなった黒谷氏らの書いた本「星と生き物たちの宇宙」は原稿のごく初期の段階で実は読ませてもらっていた。その時感想を聞かれたときは、この本はメールのやりとりで構成されているので、「なるべく著者達の私的な部分を消さないままにしておいた方が面白いんじゃないか」なんて適当なことを言っていたのだった。その著者達が書いたこの本のあとがきの言葉を最後に引用して、これからの「オッパイ星人の科学」への「戒め」と「言い訳」としておきたい、と思うのだった…
 

　科学は応用を通じて実生活に関わり、知的追求というこころの喜びにも関わる二面を持っています...多くの人に、こころを喜ばせる科学を楽しんでもらいたいですね。　　  H.Hirax, A.Kurotani