1999-01-19[n年前へ]
■小人閑居して... 
情報をポケットに入れて持ち歩きたい
ラテン語入門(http://www.hiei.kit.ac.jp/~taro/latin.html)
The Internet DictionaryProject (http://www.june29.com//IDP/IDPsearch.html)
によれば、「学者=scholar」はギリシャ語の「スコレー」を語源にしているという。語源を素直に訳せば、「暇人」となる。その中で、真理のために学ぼうとする人を「スコレー」と呼ぶのだという。
また、教育する=educateはラテン語でerudioであり、 「外に引き出す」を意味するという。生徒一人一人の中に潜んでいる才能を外に引き出す、というのが本来の意味であるという。なんとも、深い意味である。
とは言っても、昔のギリシャ人とは私は違う。「小人閑居して...」、と言う通りである。そこで、反省のために、「暇な時には真理を学んでみる」ことにした。といっても、何かを覚えるというのは面倒くさいし、無意味でもあるので、ポケットに情報を入れて持ち歩くことにした。
今回使う道具は
である。InterGetで自動巡回してダウンロードしたさまざまな情報をPalm-sizePCであるCASIOE-55の中に入れて持ち歩こうというわけである。CASIO E-55には30MBytesのCF(コンパクトフラッシュ)カードが挿してあるので、容量には結構余裕がある。
 |
Palm-size PCの便利な点であるmobile channelを自分で作成してやれば、更新も自動化できてとても便利なのだが、CFカードの領域にchannelのファイルを作成するやり方が分からなかったので、ひとまずあきらめた。大切なRAM領域を食いつぶす訳にもいかないだろう。
 |
mobile channelを自分で簡単に作成するためのMobile Channel Wizardは
http://www.microsoft.com/windowsce/downloads/pccompanions/mcwizard.asp
からダウンロードすることができる。いずれ自分用にチャンネルを作成してみたい。
まず持ち歩いてみたい資料は、RICOH情報通信研究所 有志による
英語技術文献の日本語要約(http://www.ricoh.co.jp/rdc/ic/misc/abs_club/index.html)
が面白くて良い。ここから、
- Science
- Computer Vision and Image Understanding
- Graphical Models and Image Processing
- IEEE Multimedia
- IEEE Software
- IEEE Transactions on Pattern Analysis and Machine Intelligence
 |
このボディーの中に1995-1999のScienceのアブストラクトが詰まっているのである。
あと、ゲームも...
1999-01-30[n年前へ]
■渡り鳥の秘密 
3000kmの彼方へ
先日、福島のいわき市の近くに友人を訪ねた。その近くで、はるか海を渡ってきた白鳥の群れを見た。そこでどこから来るのかとか、どうやって来るのかなどの話をした。大体、以下のような疑問である。
- Q.1:海を渡るのにどの位の時間がかかるのか?
- Q.2:位置(あるいは方向)はどのように認識するのか?
- Q.3:どこから来るのか?
- Q.4:なぜ渡るのか?
Q.3のどこから来るのかについては、仙台市科学館の中のGooseSchool(http://www.smus.city.sendai.jp/goose/home.html)に簡単な説明があった。そこにガンの「渡り」の地図が示してあった。その図を引用させて頂く。いや、もちろん「白鳥でなくガンであるし、そもそも飛んでくる場所が違う」のはわかっている。しかし、先の疑問の「どこから来るのか」はべつにいわき周辺の白鳥にこだわった疑問ではないのだから、他の場所の他の動物でもいいのだ。
 |
さて、残る疑問は、
- Q.1: 海を渡るのにどの位の時間がかかるのか?
- Q.2: 位置(あるいは方向)はどのように認識するのか?
このGooseSchool(http://www.smus.city.sendai.jp/goose/home.html)には「渡り」をどのように行うかという簡単な説明がある。それによれば、
- A.1: 人工衛星用位置送信機を取り付け経路を追跡した結果では2日間で2000kmをノンストップで渡り続ける。
- A.2: 時間は体内時計で知り,方向は星や太陽で分かる。鳥はコンパスや六分儀のような能力を両方持っている。
そこで、簡単に手に入った
- 「鳥の渡りの謎」 (ロビン・ベーカー著 網野ゆき子訳 平凡社発行 ISBN4-582-52717-5)
- 「鳥学の世界へようこそ」 (ディヴィッド・ラック著 蓮尾純子 訳 平河出版社ISBN4-89203-192-5)
「鳥の渡りの謎」の原著の表現では「渡り」を"navigation"と表現し、「鳥学の世界へようこそ」の原著の表現では"migration"と表現しているのも視点の違いとして面白い。
さて、この2冊の本はいろいろな実験を行った論文を引いて、「渡り」に関しての実証を行っている。動物が絡んだ実験は、実験の精度を高めることがなかなか困難に思えるが、そこはしょうがないだろう。というわけで、必ずしも実験が信用できるわけでもない。特に磁気に関する実験に関して精度の低さを感じる。
しかし、今回は自分で実験も解析もしていないので、簡単なまとめだけにしておく。
- 鳥(種類、地域、条件)により「渡り」の際に使用する航法(navigation)は異なる。
- 方位を頼りにするやり方も、位置を頼りにするやり方もある。使用されるのはどちらか片方のみというわけでもない。
- 位置のセンサーとしては、目印、音、におい、磁場*、重力*
- 方位のセンサーとしては、太陽の位置、光の偏光パターン、星、月などの位置、地磁気*
さて、今回は下調べばかりであった。これでは、いけない。いけない。自分で実験もしなければ意味が無い。というわけで、近日中にある実験をする予定である。
1999-03-25[n年前へ]
■電界計算をしてみたい[有限要素法編その1] 
有限と微小のパン
今回のサブタイトルは一目瞭然であるが、森博嗣のミステリのタイトルそのままである。
 |
何故、「電界計算をしてみたい-有限要素法編その1-」が「有限と微小のパン」に繋がるのか。もちろん、"有限要素法"と"有限と微小のパン"の「有限」をかけた駄洒落ではない。有限要素法を考えるとき、私は森博嗣に足を向けては寝ることができない。それが、なぜかは下の本を見ればわかる。
 |
これは、学生時代に有限要素法を勉強するために使った本である。「森 博嗣 著」と書いてあるのがわかるだろうか。いや、まさかこの本の作者がミステリを量産するとは想像もしなかった。ビックリである。講談社ノベルズと森北出版の両方から本を出している人は他にはいそうにない。
本題と関係のない話はここまでにしておく。今回はMathematicaで有限要素法を用いて静電界計算を行いたい。とりあえず、ソルバーとプリ・プロセッサまでつくる。その応用は続きの回で行いたい。Mathematicaで有限要素法を勉強するには、森北出版の依田 潔 著「Mathematicaによる電磁界シミュレーション入門」を参考にした。任意の電荷配置のPoisson方程式を解くようにしてある。
次回に詳しく計算モデルの説明を行うので、今回は計算モデルの詳細については記述しない。Notebook内に、モデルの詳細は記述してある。
このNotebookを使った計算、出力例を以下に示す。
| 平行平板電極の間に誘電体層があるモデル | 平板電極と三角柱電極の間に誘電体層があるモデル | 平板電極と円柱電極の間に誘電体層があるモデル |
 分割要素 |  分割要素 |  分割要素 |
 電位表示(色がきちんとしたhueでないことに注意) |  電位表示(色がきちんとしたhueでないことに注意) |  電位表示(色がきちんとしたhueでないことに注意) |
 半分の領域の電位を鳥瞰図にしたもの |  半分の領域の電位を鳥瞰図にしたもの |  半分の領域の電位を鳥瞰図にしたもの |
Mathematica3.0のHTML出力は大変便利だが、漢字が化けるのが困りものだ。しかも、ちょっと似た漢字に化けてしまうからわかりにくい。今回のNotebook中で化けた漢字を以下に示す。
- 油界 <- 電界
- 堰素 <- 要素
- 誘油 <- 誘電
- 姦み込む <- 組み込む
- 表傭 <- 表面
- 壓さ <- 高さ
- 堆心 <- 重心
- 肖似 <- 近似
- 内占 <- 内部
- 傭積 <- 面積
- 回寂 <- 回転
- 進当 <- 適当
- 懷瞰 <- 鳥瞰
中国語みたいな化け方である。しかも、意味としても何か変な化け方である。いつか、この対処方法と理由を考えてみたい。それにしても、週末の遊び道具としてはMathematicaは素晴らしいと思う。
1999-07-14[n年前へ]
■夏目漱石は温泉がお好き? 
文章構造を可視化するソフトをつくる
先週は新宿で開催されていた可視化情報シンポジウム'99を見ていた。参加者の世界が狭い(ジャンルが狭いという意味ではない)し、学生の発表が多すぎるように思ったが、少なくとも本WEBのようなサイトで遊ぶには面白い話もあった。というわけで、これから何回か「可視化情報シンポジウム'99」記念の話が続くかもしれない。とりあえず、今回は「小説構造を可視化しよう」という話だ。
まずは、「可視化情報シンポジウム'99」の発表の中から一番笑わせて(笑ったのはいい意味ですよ。決して皮肉ではないですよ。しつこいようですが、ホントホント。私のツボに見事にはまったのだからしょうがない。)もらった発表のタイトルはこれである。
文学作品における文体構造の可視化 - 宮沢賢治「銀河鉄道の夜」の解析-
白百合女子大学大学院の金田氏らによる発表だ。予稿集から、その面白さを抜き出してみよう。まずは過去の研究の紹介をしている部分だ。
作品(hirax注:夏目漱石の「虞美人草」と「草枕」)の始まりから終わりまでを時系列で捉えると(hirax注:話法に関する解析をすると)、二作品はともに円環構造、つまり螺旋構造を描きながら、物語が進行していくことが、四次元空間上に表現された。
中略
これは、作品の解析結果を可視化することで、夏目漱石の思考パターンと内面の揺れが明らかにされたことを意味する。
なんて、面白いんだ。この文章自体がファンタジーである。こういうネタでタノシメル人にワタシハナリタイ。おっと、つい宮沢賢治口調になってしまった。そして、今回の発表の内容自体は、宮沢賢治の「銀河鉄道の夜」の中に出てくる単語、「ジョバンニ・カンパネルラ・二」という三つの出現分布を調べて構成を可視化してみよう、そしてその文学的観点を探ろう、という内容だ。
本サイトは実践するのを基本としている。同じように遊んでみたい。まずは、そのためのプログラムを作りたい。名づけて"WordFreq"。文章中の単語の出現分布を解析し可視化するソフトウェアである。単語検索ルーチンにはbmonkey氏の正規表現を使った文字列探索/操作コンポーネント集ver0.16を使用している。
ダウンロードはこちらだ。もちろんフリーウェアだ。しかし、バグがまだある。例えば出現平均値の計算がおかしい。時間が出来次第直すつもりだ。平均睡眠時間5時間が一月続いた頭の中は、どうやらバグにとって居心地が良いようなのだ。
wordfreq.lzh 336kB バグ有り版
バグ取りをしたものは以下だ(1999.07.22)。とりあえず、まだ上のプログラムは削除しないでおく。
失楽園殺人事件の犯人を探せ - 文章構造可視化ソフトのバグを取れ - (1999.07.22)
動作画面はこんな感じだ。「ファイル読みこみ」ボタンでテキストファイルを読みこんで、検索単語を指定して、「解析」ボタンを押すだけだ。そうすれば、赤いマークでキーワードの出現個所が示される。左の縦軸は1行(改行まで)辺りの出現個数だ。そして、横軸は文章の行番号である。すなわち、左が文章の始めであり、右が文章の終わりだ。一文ではなく一行(しかもコンピュータ内部の物理的な)単位の解析であることに注意が必要だ。あくまで、改行までが一行である。表示としての一行を意味するものではない。なお、後述の木村功氏から、「それは国語的にいうとパラグラフ(段落)である。」という助言を頂いている。であるから、国語用の解析を行うときには「行」は「段落」と読み替えて欲しい。また、改行だけの個所には注意が必要だ。それも「一行」と解釈するからである。
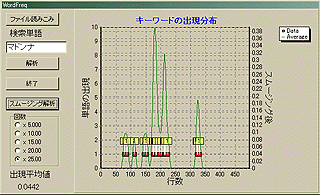 |
「スムージング解析」ボタンを押せば、その出現分布をスムージングした上で、1行辺りに「キーワード」がどの程度出現しているかを解析する。
そう、この文章は長い文章の中でどのように特定の単語が出現するか解析してくれるのである。
それでは、試しに使ってみよう。まずは、結構好きな夏目漱石の小説で試してみたい。
電脳居士@木村功のホームページ
から、「ホトトギス」版 「坊っちやん」のテキストを手に入れる。そして解析をしてみよう。まずは、この画面は夏目漱石の「坊っちやん」の中で「マドンナ」という単語がどのような出現分布であるかを解析したものである。
 |
文章の中ほどで「マドンナ」は登場してくるが、それほど重要なキャラクターでないことがわかる(このソフトがそう言っているんで、私が言っているのではない。だから、文句メールは送らないで欲しい)。
それでは、「湯」というキーワードで解析してみよう。「坊っちやん」と言えば道後温泉であるからだ。
 |
おやおや、「マドンナ」よりもよっぽどコンスタント(安定して、という意味で)に「湯」という単語は出現するではないか。出現平均値は「マドンナ」の方が多いが、安定度では「湯」の方が上だ。夏目漱石は「マドンナ」よりも「湯」すなわち温泉によっぽど興味があるようだ。
主人公を育てた重要人物「清」を調べてみると、こんな感じだ。
 |
小説の初めなんか出ずっぱりである。あと小説のラストにも登場している。
どうだろうか。見事に小説の可視化に成功しているだろう。結構、この解析は面白い。すごく簡単なのである。
これから新聞、WEB、小説、ありとあらゆる文章を可視化し、構造解析していくつもりだ。みなさんも、このソフトを使って面白い解析をしてみるとよいのではないだろうか? とりあえず、高校(もしかしたら大学の教養)の文学のレポートくらいは簡単に書けそうである。もし、それで単位が取れたならば、メールの一本でも送って欲しい。
というわけで、今回はソフトの紹介入門編というわけで、この辺りで終わりにしたいと思う。
1999-12-27[n年前へ]
■恋の力学 三角関係編 
恋の三体問題
今回はもちろん、
の続きである。前回は、恋の力学を二体間の単純問題に適用したが、今回は複雑系の入門編である三体問題に適用してみたい。二体間の単純問題から三体問題になることで、現実問題に近くなる。また、物語性も大幅にアップする(当社比)。その物語性のいい例があるので、簡単に紹介しておく。小山慶太の「漱石とあたたかな科学」講談社学術文庫の第七章に面白い話がある。- 「明暗」とポアンカレの「偶然」 - である。漱石が、明暗の中でのモチーフにしている「ポアンカレの説明する偶然」について、
- ラプラス -> ポアンカレ -> 漱石
「明暗」の中での登場人物
- 津田
- お延
- 清子
前回の「二体間の単純問題」というのは、「無人島で男と女が二人きり」という舞台設定である。現実にはあり得ない。あぁ、しまった。こう書くと、まるで今回の「三体問題」は「無人島で男二人と女一人」という舞台設定に思えてしまう。これだって現実問題としてあり得ないような気がしてしまう(関係ない話ではあるが、「無人島で男二人と女一人」という舞台設定で始まるジョークは「アメリカ人なら男同士が殺し合い、イギリス人なら紹介されるまで口をきかないから何も起きず、フランス人なら片方は恋人で片方は愛人になり問題は起きず、日本人ならホンシャにどうしたらいいか訊く。」というオチだったように思う。うーん、言い返せない。)。
だが、都会という砂漠が舞台であると思えば、東京砂漠に「男二人と女一人」、あるいは「男一人と女二人」といったような舞台設定は無理がないだろう。そう舞台は東京砂漠ということにしておこう。
それでは、考察を行ってみることにする。まずは解析の条件である。「男」と「女」に関する「恋の力」は前回と同じく、
- 「恋の力」 = 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「同性に対する反発心」 = 「相手の魅力」 * 「二人の間の距離ベクトル」/ 「二人の間の距離スカラー」
- 「恋の力」-「同性に対する反発心」 = 優柔不断度 * 「恋の加速度」
それでは、以下に計算結果をグラフにして示してみる。まずは、「女」「男1」「男2」全員が同じ資質を持つ場合である。この場合、「三すくみ」状態に陥る。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
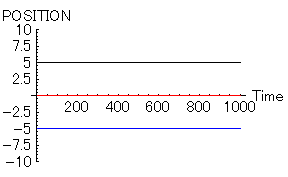 |
この「女」を中心にして、「男」達が身動きが出来なくなった状態はよく見かけると思う。ねるとんなどでよく見かける風景である。ただし、この状態が発生している理由は「男1」と「男2」そして「女」の魅力が全く同じ状態であるからだ。
ほんの少しでも「男1」と「男2」に有利な点があれば、この状態は一変する。次に示すのは「男1」が「男2」よりも1%だけ魅力がある場合である。その1%は理由は何であっても良い。例えば、偶然駅で出会ったなどでも良いだろう。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10.1,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
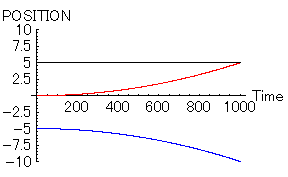 |
その一方、「男1」と「女」は幸せイッパイだろう。クヤシイくらいである。全く...
また、「女」に大きな魅力があった場合には、先の「三すくみ」状態ではなく、見事な「三角関係」に陥る。これは、三すくみ状態を打破するのに十分な魅力が「女」にあるからである。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
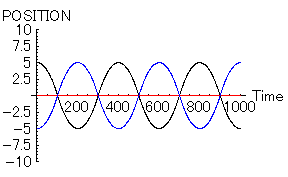 |
「女」を中心にして「男1」と「男2」が右往左往する様子が手に取るように分かる。これも世の中にはよくあるケースだろう。涙無しには見ることのできないグラフである。いや、もしかしたら、私の周りだけかもしれないが...
もちろん、この場合も「男1」と「男2」の魅力にほんの少しでも違いがあれば、状態は一変する。今度は「男2」に「男1」よりも1%魅力が多くあるものとしてみよう。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10.1,優柔不断度=10
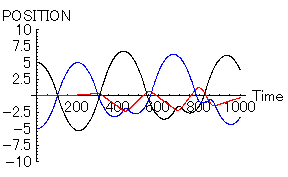 |
「女」の心が「男1」と「男2」の間で揺れ動いている様子がわかると思う。「男」は「恋の力」と「同性に対する反発心の力」により、右往左往状態である。これぞ、リアルな三角関係である。この場合、果たして「男1」が勝つのか「男2」が勝つのか、よくわからない。どの時点で「勝ち」を決めるかで大違いである。また、「女」にすらその結末は予想できないのではないだろうか。「女」自身も相手を決めた本当の理由はわからないと思われる。
これは、もう複雑の極致であるが故に、何の予想もできないのである。
ここまでの話はまるで天文学者が頭を悩ます三体問題のようである(いや、もちろんあちらが本家だが)。天文学者は天体の三体問題に頭を悩まし、我々は恋の三体問題に頭を悩ますのだ。どちらも、実にロマンチックである。
こうして、今回の話の結末はよくわからないままになってしまった。やはり、ここは「明暗」の津田のつぶやき、
「偶然? ポアンカレのいわゆる複雑の極致?なんだかわからない」という言葉で締めくくろうと思う。漱石は偉大である。
さて、「恋の力学」シリーズはまだまだ続く。近日公開とはならないかもしれないが、次回作の予告をしておこう。
- 恋の力学 運命の人編 - 偶然と必然の境界線 - (仮称)