2001-08-23[n年前へ]
■あの小判で何が買えたの? 
「夏休みの自由研究」図書館で江戸時代の物価を調べてみた
夏休みも終り、また忙しい生活が始まった。忙しい生活をしていると、「あぁ昔のノンビリとした時代、例えば江戸時代に戻りた〜い」なんて思ってしまう。江戸時代のお気楽な町人かなんかに生まれ変わって、ぼぉ〜っとしてみたり、祭りや火事に興奮してみたり、たまには働いてみたり、そして時には近所の町娘と恋なんかして過ごしてみたりしたいなぁ、と思ってみたりするのである。それに、江戸時代と言えば大昔なのだから、きっと物価はものすごく安いに違いないのである。平均給料がいくらだか知らないが、きっと色々なモノが安く買えるに違いないのだ。
といっても、私は歴史にはとっても疎い(いや違った、「歴史も」だ)ので、本当のところ江戸時代がそんなノンビリとした時代だったかどうかは知らない。まぁ、知らないからこそ、適当にこんな風に楽観的に思ってしまったりするのである。
しかし、世の中には私のような「歴史知らず人間」だけでなくて、「歩く歴史」人間のような方々も多いのである。いや、こう書くといきなり誤解されてしまいそうだ。私は別に「歩く化石」人間が多いとか、「踊るシーラカンス」人間が多いとか言いたいわけではないのである。旧人類が満ち溢れていると言いたいわけではないのである。私は、単に世の中には「歴史大好き」人間が多い、ということを言いたいだけなのだ。そう、例えば歴史大好き人間、例えば時代劇大好き人間(*1)とか幕末野郎(*2)とか戦国野郎(*3)などはきっと誰の周りにもいるハズなのである。
(*1) 古くは「杉さまぁぁ〜」と黄色い声を上げる杉良太郎大好き・時代劇大好きおばちゃん(いや、違ったおねえさん…)、など。そんな「歩く歴史」人間の方々は私を、「江戸時代はきっと色々なモノが安く買えるんだ〜。いいなぁ〜。」などと無知にも憧れたりする素直な私を、必ずやバカにするに違いない。いや、バカにされるのは構わないのであるが、そうなると、そんな自分をちょっと情けなく思ってしまう。
(*2) 坂本竜馬に自分を例える武田鉄也、など。
(*3) 会社から外へ飛び出し、その退社時に「江戸城」という本を後輩に渡して行くようなカッコイイ人、など。
そこで、今回夏休みのぼ〜っとした気分からのリハビリも兼ねて、江戸時代と現代の物価について調べてみることにした。そして、夏休み過ぎの私が夢想する「江戸時代への憧れ」がトンチンカンなものなのか、あるいはそうでないのかを調べてみたい、と思う。つまり、今回は単に「夏休みの自由研究 図書館で江戸時代の物価を調べてみた」ということなのである。そして、「江戸時代はきっと色々なモノが安く買えるんだ〜。いいなぁ〜。」の是非を確かめることにしよう。
とはいっても、じゃぁ、すぐに江戸時代の物価と現代の物価を比べよう、といきなり始めるわけにはいかないだろう。なんと言っても、江戸時代は実に長い。何しろ、江戸時代と一言で言っても、260年もあるのだ。その長い江戸時代の間にお金の価値(物価)がものすごく変化していたとしたら、一体どれが「平均的」江戸時代なのか判らない。
そこで、まずは図書館に行って、「江戸物価辞典」を片手に江戸時代の間に米の価格がどの程度変化していたのかをグラフにしてみた。江戸時代の間に物価がどの程度変化していたかを見てみるわけだ。もちろん、何をもって物価の上昇具合が緩やかなのかあるいは急なのか、という基準が必要なわけで、第二次大戦後の米価格の変化も同じように示してみた。
 |
上のグラフを眺めてみると、江戸時代(幕末期は除く)は緩やかな物価上昇は見られるが、それはごくごく緩やかなものであることが判る。何しろ200年も経っても、たかだか二倍程度にしか上昇していないのである。第二次大戦後の(すなわち、たった50年程度の間の)物価上昇に比べれば、もう物価上昇はほとんど無いといっても良いくらいである。少なくとも人生50年というような時間尺度で眺める限りは物価はほとんど変化していないのである。私の記憶(とても曖昧…)があるたった25年足らずの間に、駄菓子の価格がほとんど二倍(ガリガリ君を除く)になっているのとは大違いなのだ。ということは、少なくとも江戸時代の中期辺りの物価を眺めてみれば、それを「江戸時代」と言ってしまっても良さそうに思える。そこで、
の江戸時代中期の色々なモノの価格をグラフにして並べてみる。また、それらのモノが西暦2001年の現在、何円くらいであるかを私の主観によって判断し、同じようにグラフにしよう。そして、それぞれを比較して、- 今の方が安いモノ
- 昔の方が安かったモノ
とはいえ、もちろん江戸時代にあったが現在はもうほとんど存在しないというようなものも多い。そこで、そういうものは現在における相当品で、例えば
- 富くじ → 宝くじ
- 吉原高級遊女 → 銀座の高級?クラブの基本料金
- 町駕籠 → タクシーの初乗り料金
- 夜なきソバ → 近所のチャルメラ・ラーメン
- 絵本 → 写真集
- 貸し本 → レンタルビデオ
- 夜鷹 → ○×△■
また、モノの価格だけでなく「収入」の基準もやはり必要なわけで、それに対しては大工日当を用いた。つまり、収入の基準との大工日当に対して、色々なモノがいくらであるかを、江戸時代と現在とで比べてみることになる。というわけで、そのグラフが以下である。
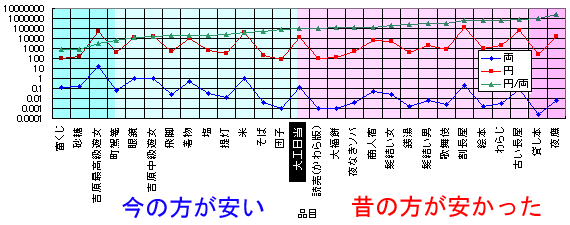 |
このグラフを見ると、例えば大工日当を基準にすると、一両はほぼ十万円に相当することが判る。また、砂糖などは今のほうが江戸時代よりもよっぽど安い。だから、砂糖を基準にすれば、一両は千円にしかならない。逆に夜鷹を基準にしてしまうと、何と一両はおよそ百万円に相当するのである。それほどに江戸時代の夜鷹は安かったのだろう。大変な話だ…。
砂糖も含め、眼鏡とか町駕籠(タクシー)とか飛脚(宅急便)とか提灯(懐中電灯)とかの、いわゆる科学の力を有効活用したものは当然現代の方が安い。そして、わらじとか歌舞伎とかの現代においては希少価値の高いものは江戸時代の方が安かったのも当然である。じゃぁ、吉原高級遊女(銀座の高級?クラブの基本料金)と吉原中級遊女(銀座の大衆クラブ)の価格の違いはどう説明するのかいう疑問も当然湧いてくるわけではあるが、そういう話はどうでも良いのだ。
何はともあれ、タクシー(町駕籠)に乗って銀座のクラブ(吉原高級遊女)に遊びに行くのが大好きな人、しかも眼鏡をかけてて、甘いもの(砂糖)が大好きなんて人には江戸時代はどうも合いそうにない。そんな人たちはすごくお金持ちでないと、江戸時代はかなりツライ時代のようである。そんな人達は、江戸時代よりも2001年現在の方が幸せに違いない。そんな輩には江戸時代はマッチしないハズなのである(根拠薄弱)。
しかし、広い風呂(銭湯)が好きで、夜のチャルメラ・ラーメン(夜鳴きソバ)にロマンを感じ、写真集(絵本)が欲しいけど高くて買えないワタシのような人間にはやはり江戸時代がジャストフィットするに違いないのだ。チープにお気楽に生活できるかもしれないのである。やはり、「江戸時代はきっと色々なモノが安く買えるんだ〜。いいなぁ〜。」は合っていたのである(ウソ)。
よっしゃぁ、私に合う時代はやっぱり江戸時代なのだぁ、とここまでは思ったのだが、もう少し私の生活パターンを考慮して吟味し調べてみると(調べなくても判るだろうが…)、江戸時代には発泡酒はもちろんビールは日本では一般的ではなかったのである。これでは、ビール(だけどお金が無いから発泡酒に変わったが)大好き人間の私としては致命的にマズイのであった…。う〜ん、う〜ん、ちょっと残念なんだけどだなぁ…。
2001-09-20[n年前へ]
■A3用紙の広さの世界 
Mosaicism
ここ数年、毎日色々な画像をプリントアウトする日が続いている。本当のことを言えば、そんな毎日に時々は飽きたりもするのだけれど、そんな風に思う時間がそんなに長いわけではなくて、結構そんな毎日が好きなのもまた事実だ。
そんな毎日なので、CRTをみながら画像を編集・加工したりする作業をすることも頻繁にある。仕事柄、割に大きな画像を処理していることも多くて、例えば最近はA3用紙程の大きさの画像をせっせと加工したり出力したりしている。しかも、単にサイズが大きいだけではなくて、解像度も高い時には4800dpi程とかなりの高解像度で作業をすることもある。A3用紙で4800dpiともなると、8000x 57000 = 46億 pixel 程になるので、いくら速いPC(WS)でもやはり処理待ちの時間があまりに長くなってしまい、モニタの前でぼんやりとしてしまうことも多い。少し前、やはりそんな作業をしている時に、モニタの前でおかしなことを考えていた。
今眺めている画像の中に含まれている46億 pixelというとほんの少し前の地球の人口くらいだろう。今の地球の人口は60億人強くらいだろうが、数としてはやっぱりそれほど違わないように思う。つまりは、A3用紙を4800dpiで出力する時には、地球の全人口に近いくらいの点がA3用紙の広さの世界に塗り込められていることになる。それはまるで、A3用紙の広さの世界に、地球上の人間一人一人がそれぞれの色を出しながら立っているのと同じようなものかもしれない。なんてそんな風に考えてしまったのである。ほんの小さなA3用紙の中に、地球上の人間全員で描くモザイク画を想像してしまったのである。
だけど、「地球上の人間全員で描くモザイク画」の中では一人のドットは遥かに小さくて、4800dpiの小さなドットはの情報なんか消えてしまって、やっぱりそんなA3用紙の中に立つ一人一人は見えないのだろうか、とも冷静に考えたのだけれど、やっぱりそれは違ことに気づいた。
何しろ、その「地球上の人間全員で描くモザイク画」をよくあるプリンターなどの600dpi程度の解像度に縮小してみたところで、元のごく小さな4800dpiの1ドットの情報が消えてしまうわけではない。600dpiは4800dpiの1/8ということで、4800dpiの8x8=64ドットが600dpi1ドットに縮小されることになる。4800dpiの1ドットの本来の色が64分の1の薄さにはなるけれど、それでもそんなちっちゃな点の情報もちゃんと残っている。だから、A3用紙の広さの画像を虫眼鏡で眺めてみれば、そんな狭い世界の中にでも、やっぱり地球上の人一人一人そのものが点描となって描かれているモザイク画が見えるのかな、とか考えたりした。
2002-02-11[n年前へ]
■めがねっこ大好き。 
めがねを外すと美人になるは本当か!?
理系=めがねっこ大好き? 「どんな時に自分を理系だと思う?」と文系人間に聞かれた。私は「うむむ…」と答えに詰まってしまった。そんな私に、その文系人間はまるで勝ち誇ったような表情で「じゃぁ、理系と文系はどう違うと思う?」と畳みかけるように聞いてきた。この手の数限りなくある、「理系と文系」「男と女」はどう違う?という問いには立ち入ってはいけない、というのが私の家の代々の家訓なのであるが、ここで黙りこんでいては「勝ち負け」でいうところの「負け」だと思ったのか、理系の誇りを守るべく、私の口がいきなりしゃべり出した。
例えば、建築で言えば、鉄骨建築が理系で、プレハブ住宅が文系なのである。体で言えば、皮膚の感覚を大事にするのが文系で、骨から組み立てていくのが理系なのである。つまり理系は骨があるのである。そして、詩で言えば、散文詩は文系で定型詩が理系なのである。つまり、理系は型にこだわる部分があるのである。と、スキーのモーグル競技でコントロールを失い、コースアウトしてしまう選手のように私の口は暴走を続け、理系=めがねっこ大好き、という辺りではもう「勝ち負け」でいうところの「負け犬」であるようにしか思われず、理系の誇りを守るどころか、理系を単に汚しただけに終わってしまった。そこで、悔しさのあまり、今回は「めがねっこ」に対し理系的なアプローチで近づいてみることにした。そして、私が汚してしまった理系の汚名をすすぎたいと思うのである。だから、例えば理系は女子高生の制服が大好きなのである。色々ある女子高生をセーラー服(あるいはブレザー)という記号で記号・集合論的に取り扱うことを可能にし、その記号を言葉にし、ついにはその制服を見るだけで萌えることができるのである。それが理系なのである。
つまりは、「このアイドルがなんとなく好き」というのが曖昧模糊としたものが文系であるならば、「このアイドルがめがねっこだから好き」という確固とした意志それすなわち理系なのである。理系=めがねっこ大好きなのである。
「めがねを外すと美人になる」は本当か!?
よく、少女マンガなどで、「ヒロインが眼鏡をとると美人になった」というストーリーをみかける。今はどうだか知らないが、少なくとも昔はよくそんなストーリーを見かけた。あれは果たして本当だろうか。そして、それが本当であるならばそれは一体どんな物理現象なのだろうか?そして、ヒロインが眼鏡をとると美人になった」というストーリーと「めがねっこ大好き」というそ相反する二つの事象はどんな原因に基づいているのであろうか?それを理系的なアプローチで明らかにしてみたいと思う。
めがねはもちろん視力が悪い場合に、その矯正を行うための道具である。近視の人であれば矯正のために凹レンズをかけるし、逆に遠視の人は矯正のためには凸レンズをかける。凸レンズと言えば、虫眼鏡と同じで、何かの近くにレンズを持っていけばそれが拡大されて見える。また、逆に凹レンズであれば、対象物が小さく見える。
 |
だから、近視の人が凹レンズである眼鏡をかけた場合には、その人の目が他の人からは小さく見えてしまうのである。実世界でも、少女マンガの世界でも大きな瞳は美少女の象徴であるが、近視の人が眼鏡をかけると、大きな瞳を持つ美少女でもちっこい瞳になってしまうのである。
試しに、仲間由紀恵に凹レンズの眼鏡をかけさせた場合の、シミュレーションを行ってみたのが下の結果である。左のめがねをかけた「近視の」仲間由紀恵は確かにキレイではあるけれど、右の仲間由紀恵の方が、美少女という魔性の魅力という点で遙かに勝っていることが判るだろう。
 |  |
そう、近視の人の場合には、「めがねを外すと美人になる」は物理的に本当なのである。近視の人の割合は国によって大きく違うらしいが、少なくとも現代の日本では近視の人の割合は圧倒的に多い。ほとんどの人が近視である、といっても良いくらいである。ということは、そんな日本では「めがねを外すと美人になる」はかなりな確率で事実である、と言えるわけだ。
それでは、「めがねを外すと美人になる」ということと相反するとしか思えない「めがねっこ大好き」現象をどう説明したら良いだろうか?一つは、遠視の場合先の近視の場合と逆のことが起きる、ということである。すなわち、遠視の人の場合には、眼鏡をかけると瞳が大きく見えるのである。すなわち、眼鏡をかければ、美少女の象徴たる大きな瞳が手に入るのである。
下の「遠視の」仲間由紀恵の場合の眼鏡シミュレーションを見てみると、めがねをかけたことでずいぶんと美少女度がアップしていることが判ることと思う。まさに、その瞳には魔性の魅力が宿っているとしか思えないほどなのである。
 |  |
ということは、「眼鏡を外すと美人になる」は本当。ただし、近視の人の場合は、ということなのだ。そして、もし遠視の人であれば、「眼鏡をかけると美人になる」が本当なのである。
とはいえ、日本人では遠視の人は少ないわけで、それではめがねっこを増やす原因たる「眼鏡をかけると美人になる」が少なくなってしまう。そこで、他の原因を考えてみると、例えば近視の人が裸眼の時には瞳の口径を小さくすることで、被写界深度を深くする、すなわちハッキリとものを見ようとして、目を細めがちであること、すなわち小さな瞳になりがちであること、なども原因の一つとして考えられるだろう。
そしてまた、実は近視の程度が低い場合には、「めがねっこ大好き」現象を支えるもう一つの事実がある。レンズの度数がきつくなくて、他の人から見た瞳の拡大縮小が行われないような場合にも、眼鏡をかけると実は心理的に瞳の大きさが変わって見えるのである。
下の「目が小さい」仲間由紀恵は左右で目の物理的な大きさは完全に同じである。が、心理的には結構違って見える。眼鏡をかけた仲間由紀恵の方が目が大きく見えることが判ると思う。「目が小さい」場合、めがねをかけると瞳が大きく見えるのである。
「目が小さい」仲間由紀恵  | 「目が小さい」仲間由紀恵  |
日本人は目が小さい人が多いから、このような眼鏡をかけると心理的に瞳が大きく見える影響は無視できないに違いない。
ところが、目がもともと大きい場合には、この現象はそれほど大きく現れるわけではない。もともと瞳が大きいがために、眼鏡をかけたからといって割合的にそれほど瞳が大きく強調されたりはしないのである。その例を下に示す。下の二枚は目の物理的な大きさは完全に同じなのであるが、心理的に受ける瞳の大きさ=美少女度の違いは上の例ほどではないことが判るだろう。
「目が大きい」仲間由紀恵  | 「目が大きい」仲間由紀恵  |
ということで、
- 瞳が多きい近視の人の場合、眼鏡を外すと美少女になる
- 目が小さかったり、遠視だったりする人の場合、「めがねっこ」=美少女になれる
ところで、理系と文系…
さて、理系的「めがねっこ大好き論」も良いのだが、話をそもそもの「どんな時に自分を理系だと思う?」という問いに戻ろう。
よく私が見かけるパズルは大抵が論理的なパズルだ。論理的=理系ではないから、それを理系パズルと呼ぶのはいけないと思うが、あえてそれを理系パズルと呼んでみる。間違っているのを承知で、あえてここではそう呼んでみる。
そんな理系のパズルでもやっぱり色々あるだろう。大抵のそんなパズルの答えは答えがただ一つに限られるものだろうが、時にはその答えが無限にあるものもあるかもしれない、そして答えが一個もないパズルだってあるかもしれない。そしてまた、「答えを見つけられないこと」を証明できるようなパズルだってあるだろう。だけど、いずれにせよ、そのパズルを解く過程で現れようとする「割り切れない何か」は「それが割り切れる軸」を駆使することで、巧妙に消し去っていくことができる。だから、とてもそれは結構気持ちが良い作業だ。少なくとも、私にはそうだ。あるいは、答を判定するものが、自分ではない論理なり自然現象に任せられているから楽なのかもしれない。
だけど、もしそんな論理的なパズルとは違う非論理的なパズル、ここではあえて文系のパズルと呼ぶようなものがあったとしたら、その答えは「割り切れない何かを拾い集めたようなもの」であるような気もする。そして、その解く過程はもしかしたら割り切れない感情や雰囲気を拾い集めて、割り切れないままに何とか答えを投げ出しいく作業であったりするのかもしれない。それに、そこでは答を判定する何かなんかそもそも存在しないか、あるいはその判定する何かが人であるのかもしれない。
私には、そんな「割り切れないままに何とか答えを出していく作業」はちょっと辛いなぁと思う。やっぱり、私は理系パズルの方がずっと楽で気持ちが良い。だから、今度「どんな時に自分を理系だと思う?」と聞かれたら、そんなことを上手く言えたらいいな、と思う。いつも、思い浮かべたことを伝え続けたいな、と思う。
2002-06-03[n年前へ]
■カードサイズの「画像探偵セット」!? 
お手軽線数メーターを作るのだ
「どんなものでも、自分の目で眺めてみた〜い」と、ワタシはいつでも思う。世の中スベテのものを、自分の目で眺めてみた〜いと思う。しょんべん小僧が空中に描き出す放物線、巨乳ギャルにロックオンするオッパイ星人の目の動き、ビデオにかかるモザイクの向こう、はたまた田代まさしが恋い焦がれるミニスカートの結界の秘密、とにかく世の中のものスベテを何でもかんでも眺めてみたい、覗いてみたい、とワタシはいつも思っているのである。(とはいえ、誤解されると困るので念のために書いておくが、もちろんミニスカートの中を覗いたりはしないのだ)
そんなわけで、ワタシのケータイのストラップには「ちっちゃなちっちゃな虫メガネ」がついている。この虫メガネを武器にして、ワタシは色んなモノを覗くのがクセになっている。スーツ姿で出張している時だって、おもむろにこの虫眼鏡を取り出して、色んなものを覗いてみたりしているのである。
 |
だから、毎朝届けられる新聞に折り込まれているチラシやカタログを眺めるときだって、そんなカタログに「ちっちゃなちっちゃな虫メガネ」を向けてみて、その「虫メガネ」を通して、カタログがどんな風に印刷されているかをよく眺めてみる。下の左のようなカラーの綺麗なカタログだって、「虫メガネ」を通して眺めてみると、右の拡大写真みたいに、四色(シアン、マゼンダ、イエロー、ブラック)が規則正しく並んでいるようすが見えてくるのである。離れてみればキレイな写真が「虫メガネ」を通して眺めてみるだけで、こんな風に様子が変わるなんてとても不思議な気分になったりするのである。まるで、女性の化粧のように不思議で、こんな四色の手品はとても面白いのである。
| (左上と右上部分はマゼンダとシアンだけを見やすくしてみた)
|
で、こんなカタログの拡大図を眺めていると、四色に分けられた色がどんな風に並べられ形作られているかを、知りたくてたまらなくなったりする。つまり、「どんな間隔でこの色は配置されているのだろう?」とか「一体、どんな角度でこの色は並べられているのだろう?」とか思うわけである。もちろん、この画像に二次元フーリエ変換などをかけさえすれば(周波数解析をすれば)、「どんな角度で・どんな間隔で色が並べられているか」ということは知ることができるけれど、まさかワタシの頭の中でそんな作業ができるわけはない。かといって、このカタログを読み込むための「画像読みとり装置」や「解析をするためのコンピューター」を毎日持ち歩くなんてこともできるわけもない。
そこで、「どんな間隔でこの色は配置されているのだろう?」とか「一体、どんな角度でこの色は並べられているのだろう?」とかいう疑問の答えがすぐ判るように、先日こんなカード、ぴったりクレジットカードサイズの透明シートに規則的なパターンを印刷したカード、を作ってみた。名付けて、Peco-Chartなのである。
これはもちろん、判る人には判るだろうが、ハンディ「線数メーター」というモノである。一言で言えば、画像の周波数解析をとっても簡単にすることができる手品の小道具のようなカードなのだ。
 |
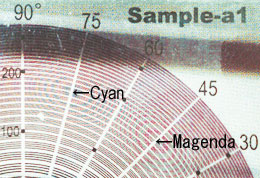
例えば、さっきのカタログの上にこのPeco-Chartを重ねて置いてみると、アラ不思議、何やらヘンな模様、不思議なモアレ模様が浮かび上がってくる。下の左の写真、あるいは右の拡大写真を眺めてみればマゼンダとシアンの同心円がハッキリと浮かび上がっているのが見えるだろう。例えば、シアン色の場合は75°の角度で175線(175線/inch)位の位置、そしてマゼンダ色の場合は45°の角度で同じく175線位の位置を中心として、同心円状のモアレ模様が浮かび上がっている。
つまり、「このカタログはシアンは75°の角度方向に1インチ辺り175個のドットが並べられていて、マゼンダのドットは45°の角度方向に並べられている」、ということを、このPeco-Chartを重ねて置いてみさえすればたちどころに知ることができるのである。
 |  |
 |
こんなペラペラのカードで周波数解析ができるなんてとても不思議に思えたりもするけれど、ちょっと考えてみればこれはごく当たり前の話である。
でも似たようなことをしたように、モアレというものは「二種類以上の何らかの模様(パターン)が干渉して発生する」ものである。つまり、ある意味「二つのパターンの相関をとる」ということである。そしてまた、少し考えてみれば「画像の周波数解析」というものは「対象となる画像」と「基準関数(三角関数etc.)」の間で相関を調べることと同じである。だから、「基準となるパターン」を「対象となる画像」の上に重ねてみた時に見えるモアレのパターンは「対象となる画像」の周波数解析結果を実は示していると考えてみても良いのである。だから、このPeco-Chartはクレジットカードサイズのペラペラなちっぽけなヤツではあるのだけれど、実は色んな画像の周波数解析をしてくれるスゴイヤツだったのである。そして、こんなポケットに入るほど小さい線数メーターははなかなか無いので、、カード入れからコイツを華麗に取り出してみせたりすると、うらやましがる人もとても多く(仕事柄、画像出力に関わる人達が多いから)、なかなかに気持ちが良いのである。 とはいえ、自慢してばかりでは何なので、さらに大量に配布すべく新たなPeco-Chart二号機をデザインしてみた。それが、下の名付けてPecochartproである。
 |
このPecochartproの謳い文句はその名の通り「プロ仕様」というわけで、画像出力に関わっている何人ものベータテスター達(自分も含めて)の感想をもとにして、
- 70線から350線までの線数とスクリーン角度の測定ができる「線数・角度メーター」(分解能を2線単位から1線単位へと二倍向上、スクリーン角度のガイドは2.5度刻み)
- 90線から410線までの線数を高精度(0.25線刻み)に計測することができる「線数メーター」(新機能)
- 線・文字の太さを計測できる「線幅スケール」(新機能)
- 〜30級、〜30ポイントまでの文字サイズ(級数、ポイント)測定ができる「文字スケール」(Peco-Chartと同じ)
- 「8cm定規」(Peco-Chartと同じものを使い勝手はそのままにコンパクト化)
- そして、便利な「画像に関する換算表」(内容を従来比75%増量)
それにしても、何か自分に役に立つツールを作るというのは本当に楽しい作業だった。手作りツールぎゃらりい脇色彩研究所ではないけれど、こんな「hirax.netオリジナルグッズ」をいっぱい作って「探偵セット」ならぬ「できるかな?セット」として、面白メールをくれた方にプレゼントとかしてみたら楽しいんだろうなぁ、と思うのである。というわけで、そんなツールをせっせと作るのだぁ、なんてことを実は計画中なのでした、ハイ。
2002-11-30[n年前へ]
■ウェブサイト・アーカイブ(仮) 
これはとても役に立ちそうな「ウェブサイト・アーカイブ(仮)」。で、おおぅhirax.netもあるぞ、と眼鏡っ娘論の中に…。

