1999-02-28[n年前へ]
■分数階微分の謎 
線形代数、分数階微分、シュレディンガー方程式の三題話
分数階微分?
InterLabの1999No.5を読んでいると面白い記事があった。いわき明星大学理工学部の榊原教授の「Waveletと数式処理ツール」という記事である。といっても、興味を持ったのはWaveletのことではない。もちろん、Waveletに興味がないわけではない。この榊原教授が講師を務めたWavelet講習にも参加したこともある。しかし、今回興味を惹かれたのはその記事中にあった「分数階微分の解析」である。InterLabの榊原教授の記事を引用すると、-通常微分・積分は整数回実行できるが、分数階微分はこれを分数に一般化したものである。さまざまな物理や工学の現象の記述に使われるようになった-とある。一階微分とか二階微分というものはよく使うが、0.5階微分などというものは使ったことがない。どのようなモノなのかさえよくわからない。
参考:
一体、どんな物理や工学の現象の記述に使われているのか知りたくなったので、infoseekで調べてみる。すると、いわき明星大学の清水・榊原研究室の「粘弾性動モデル」が引っ掛かる。
参考:
衝撃吸収・シリコーンの弾性率などに興味を持っている人には面白いかもしれない。もう少し調べてみると「バナッハ空間バナッハスケールにおける分数階積分作用素」というようなキーワードも引っ掛かる。
そこで、まずは勝手に分数階微分について考えてみた。
分数階微分・積分の勝手な想像図
まずは、イメージを考えるためにグラフを作成してみる。x^2の関数、および、それを微分・積分した関数である。微分は3階まで、積分は2階まで行っている。
 |
このグラフ形式の表示をちょっとだけ変えてみる。
 |
ここまでくると、平面グラフにしてみたくなる。つまり、微分・積分の階数を離散的な整数値でなく、連続的な値としてのイメージに変えたくなる。
 |
これで、微分・積分が整数階でない場合のイメージ(勝手な)ができた。微分・積分が離散的なものではなくスムーズにつながっているものであるというイメージである。図.2から図.3への変化をよく覚えていてほしい。
といっても、これは数学的なイメージのみで物理的なイメージはまだここでは持っていない。位置、速度、加速度などの微分・積分で選られるものに対して同じようなイメージを適用すると、位置なんだけれどちょっと加速度っぽいもの、とか、速度と加速度の「合いの子」みたいなものというような感じだろうか?
さらに、これから先は、f(x)という関数が示す無限個の値を位置ベクトルと考えて、f(x)というのは無限次元空間の一つの点だというイメージを持つことにする。線形代数を考えるならそれが一番わかりやすいだろう。任意の階で微分された関数群が集まって、さらに高次元の空間をなしているというイメージである。
分数階微分を調べる
勝手なイメージはここまでにして、手元にある数学の参考書の中から手がかりを探してみた。すると、大学院入試問題解説 - 理学・工学への数学の応用 - 梶原壌二 現代数学社ISBN4-7687-0190-6
の中に手がかりがあった。あれ、ということは以前にやったはずなのか...そう言えばおぼろげな記憶がちょっと...
その中の言葉を少し引くと、
フーリエ変換は等距離作用素である、関数空間L^2(R)における回転といえる。結局、
となる。そして、古典力学におけるハミルトン関数において、運動量を微分演算子で置き換えれば、量子力学や量子化学のハミルトン演算子が得られ、シュレディンガー方程式などにつながるのである、とある。他の資料を眺めてみると、どうやら量子力学などの分野からの要請に応じてここらへんの微分演算子の分野が発展しているようだ。理論物理などをやった方ならよくご存知のことだろう。例えば、水素原子の基底状態の波動関数へ運動エネルギーの演算子を作用させるというような、基本的な所でも、このフーリエ変換を用いた微分演算が用いられてる。ここで、fは元の関数であり、Fはフーリエ変換
さて、この式自体は非常に簡単である。それにイメージも湧きやすい。
i を掛ける演算、私のイメージでは複素数空間の中で90度回転をする(言い換えれば、位相が90度ずれる)演算、が微分・積分であるというイメージはスムーズに受け入れやすい(それが正しいかどうかは知らないが)。なぜなら、微分が空間の中での回転であるとすると、三角関数の微分・積分に関する性質(例えば、Sinを微分するとCosに、Sinを2階微分すると-Sinになる、すなわち、一回の微分につき位相が90°ずつ回転する(位相がずれる)というような性質)が納得でき、それがフーリエ変換という形で登場してくることがスムーズに受け入れられるのである。また、微分といえばとりあえず三角関数の登場というイメージもある。
もう少しわかりやすく書くと、
- 三角関数では一階微分の結果は90度位相がずれる(回転する)。
- ならば、(例えば)0.5階微分は45度位相をずらせば良い。
- 任意の関数もフーリエ変換により、三角関数に分解される。
- ならば、任意の関数に任意の実数値の微分が成立する。
任意の関数をフーリエ変換し三角関数に分解した時の位相、言い換えれば、周波数領域での位相ずらし、で分数階微分が定義されるということは、物理的実用的に大きな意味を持つ。例えば、電磁波、弾塑性運動などの物理現象の中での位相変化を分数階微分で解けることになる。例えば、複素貯蔵弾性率などについて分数階微分との関係は深そうである。あるいは、媒体中の電磁波の位相などについて適用するのも面白そうである。
分数階微分を使ってみる
よく分からないところも多いが、とりあえず、
という式を使ってみる。まずは、使ってみないとわからない。とりあえず、1次元の関数を作成して、この式を適用してみる。まずは、よく出てくるガウス分布で適用してみる。まずはガウス分布とそれの通常の一階微分の解析解を求める。
 |  |
それでは、今回の方法による一階微分の結果と、それと解析解との比較を示す。なお、本来無限領域のフーリエ変換を有限の領域で行っているため、端部近くで変なことが生じるのはしかたがないだろう。また、色々な事情により係数の違いは無視して欲しい。
 |  |
ちょっとずれが生じているが、こんなものだろう。しかし、これだけでは今回のフーリエ変換を用いた微分の面白さはでてこないので、0から2の範囲で連続的に分数階微分をしてみる。
 1/10 (=0.1)階微分 |  1/2 (=0.5)階微分 |  7/10 (=0.7)階微分 |  1階微分 |
 13/10 (=1.3)階微分 |  15/10 (=1.5)階微分 |  17/10 (=1.7)階微分 |  2階微分 |
モーフィングのようで面白い。
さて、今回は分数階微分を勉強してみる所までで、これの応用は別に行ってみたい。もちろん、言うまでもないと思うが、間違いは多々あると思う。いや、田舎に住んでいるもので資料がないんですよ。
2000-02-07[n年前へ]
■記憶の中の風景 
Photoshopで美術遊び 水彩画と色鉛筆 編
大学時代のとある日にCanon Ftbというカメラをゴミ捨て場で拾ってから、写真が私の趣味の一つになった。大学院に入る頃には、使われていなかった暗室と写真焼き付け機をも研究室の地下で見つけ、せっせと写真を焼き付けることも大好きになった。その暗室は怪人二十面相が登場しそうな古〜いレンガ造りの建物の地下にあって、実に不気味な場所だったのだが、全然気にならなかったのが今から考えるにとても不思議だ。
私が拾ったFtbはいつの間にか壊れてしまったから、他のカメラを買ったり(それでも中古だったが)、交換用のレンズを買ったりということはした。しかし、私の興味は風景や被写体の方には向いたが、カメラやレンズあるいは暗室機材といったものに対してはあまり物欲がわかなかった。
そんなことを思い出したのは、私の職場の人達がCanon EOS D30(358000円ナリ)を買ったり、EF300mmF2.8L(690000円ナリ)を買ったりと、物欲大魔人に変身していたからだ。まるで、「この世の終わりまであと一ヶ月」の「宵越しの金は持たない江戸っ子状態」で買い物をしまくっているのである。マジメに、「こ、この世の終わりが来るのですか?」とか、「あそこに見える富士山はヤッパリ噴火するのですか?」はたまた、「あなたは実はスタパ齋藤なのですか?」とかおそるおそる尋ねたくなるホドなのである。
ところで、ふと気付くと時はすでに二十一世紀になっていて、持ち歩いていたEOS620はデジタルカメラのFinePixに代わり、数学教室の地下にあった暗室はノートPCの中にあるPhotoshopに変わってしまっている。そんなことをつらつらと考えていると、ちょっとセンチメンタルな気分になったので、今回は暗室で印画紙上に浮かび上がる画像を眺めていた頃を思い出しながら、photoshopで少し遊んでみることにした。(こんなに無意味に前振りを書いたのは、そんなに大した話じゃないけどセンチな気分なのだから勘弁して欲しい、という気持ちである。)
写真というのは何の考えも無しに撮ってしまうと、不必要にリアルになってしまう。不必要にリアルということは、逆に必要なところがリアルでなくなってしまったりする。あまりにリアルすぎて、「記憶の中の風景」とは違ってしまったりするのである。そうなると、私にとってはリアルな「昔見た風景」ではないのである。私の中の記憶が間違っているといえばそれまでなのだが、私の中ではその記憶が基準なのだ。
そんな時、いっそのこと写真を絵画風に加工して、私の「記憶の中の風景」に合わせてしまおうかと思うことがある。写真を絵画風に加工するソフトというのはたくさんあるので、そんなことは簡単にできてしまう。Photoshopに含まれているフィルターでもそれっぽい(かなり不十分な機能ではあるが)ものはたくさんあるし、サードパーティー製のプラグインもたくさんある。そしてまた、インターネット上の情報でも、「絵画風&ソフトフォーカス(デタラメPhotoshop)」などがある。そんな中でも、特にこのVirtualPainterなどはかなりスゴイ。いくつかの処理ができるのだが、その中でも特にこのPlince(色鉛筆風)とRabica (水彩画風)の二つはとてもきれいである。
 |  |
 |  |
ソフトが勝手に自動変換したとは思えないくらい、なかなかスゴイできばえである。最初見たときはちょっとビックリしたほどだ。少なくとも私が色鉛筆や絵の具の筆を手にしても、こんな絵は書くことができないに違いない。いや、正直に言えば「できないに違いない」どころではなくて、「できない」のである。
ところで、このソフトはシェアウェアで、未だ購入していないので画面中に「Unregistered」という文字が恥ずかしくも輝いている。もちろん、素晴らしいソフトなので買うつもりではあるのだが、他人様の作ったソフトをただ使うのは今ひとつ面白くない。まずは、自分自身で同じようなことができるかどうか挑戦して、そしてできることならば自分の好きなような効果が出るようなプラグインなりソフトを作ってみたい。
というわけで、自分の頭を整理するために、まずはPhotoshop5.5単体を使って、この二つの処理と似た処理をしてみることにした。まずは簡単そうな水彩画風からだ。
下の写真はメキシコのティファナで撮ったよくある街並みの写真だ。何の変哲もない写真ではあるが、実はこの直後にデジカメを道路に落としてしまって、私のデジカメ様はこの後お亡くなりになってしまったという、私にとってはとても哀しい写真なのである。
 |
さて、この画像を水彩画風に変換する時の方針は、
- 色が付いてる部分は、水彩絵の具で塗りつぶす。つまり、階調性をなくして、境界はにじませる。
- 細かな部分は鉛筆で書くから、シャープに書く。
そして、水彩絵の具っぽくするために、CMYチャンネルを選択して、「フィルタ→ノイズ→ダスト&スクラッチ」をかける。そうすると、もうかなり水彩画調に感じられるようになる。そして最後に水彩絵の具のにじみを再現するために、CMYチャンネルのみに「フィルタ→表現手法→拡散」あるいは、ランダムのグレーノイズを2チャンネル分用意して、「フィルタ→変形→置き換え」でにじみを表現しよう。ちなみに、今回は「フィルタ→変形→置き換え」の方を使ってみた。ここで、「フィルタ→ブラシストローク→はね」はCMYKモードでは使えなかったので、残念ながら却下である。また、色モード変換時に彩度が低下するので、彩度アップは適時しておいた方が良いだろう。
こうして、紙の漉き目に沿った水彩絵の具のにじみも処理すると下のような画像が出来上がる。「できるかな?」の色鉛筆風のメキシコのティファナの風景である。
 |
私のセンスがいまいちなのはさておき、水彩画風にする処理としてはまぁ許せるレベルだと言えるかもしれない。処理自体は何段階もあるが、アクションファイルでも作ってやれば、簡単にできると思う。
さてさて、このイキオイで一気に色鉛筆風も片づけてしまおう。こちらの色鉛筆風の方針は、
- 画像を何色かに分解して、その色で斜線をひく。
- 色が濃い部分は別の角度からも線をひく。
- 細かい部分は黒鉛筆で少しだけシャープな線を入れておく。
まずは、まずは「イメージ→色調補整→色相・彩度」で彩度を最大にする。「イメージ→色調補整→トーンカーブ」で少し明るめの画像にする。次に、「フィルタ→ピクセレート→点描」で、何色かの色に分解しつつ、なおかつ点画像にすることであとで色鉛筆風の斜線に変形する準備をしておく。そして、「フィルタ→ブラシストローク→ストローク(斜め)」で点を斜線に変形させ、その後「フィルタ→シャープ→アンシャープマスク」をかけて、エッジをシャープにして、色も鮮やかにして色鉛筆っぽくする。また、現画像を「イメージ→色調補整→トーンカーブ」ですご〜く明るめの画像にしたものに対して、同様の処理をかけて(ただし、斜線の角度は変え)、先程の画像にαチャンネルで重ね合わせる。また、現画像を「イメージ→色調補整→トーンカーブ」でものすご〜く明るくしたものもさらにαチャンネルで重ね合わせる。
この色鉛筆風の処理のコツは点描で分解して、ストローク(斜め)+アンシャープマスクで長めの鮮やかな線にすることである。
すると、こんな感じで「できるかな?」の色鉛筆風の藤原紀香のできあがりである。Photoshop付属のフィルタだけで処理している割には、なかなか良い感じのできに思えるのだが、それは単に藤原紀香の色香に惑わされているだけかもしれない。
 |
今回は、写真画像を会画風にするためにはどんな処理をすればよいかを考えるために、Photoshopの内蔵フィルタだけを使って処理してみた。次回は、今回考えた処理の流れを自作アプリで組んでみたいと思う。そうそう、あと「こんな処理をしてみたい」という希望メールも大歓迎です。そういう希望を教えていただければ幸いです。だからといって多分何をするわけでもありませんが、ハイ。
2001-01-21[n年前へ]
■カンバスから飛び出す「名画の世界」 
作者の視点から眺めてみれば
先日、新穂高ロープウェイスキー場へ行った。雄大な景色に囲まれたとても素晴らしいスキー場だ。その景色を思わずデジカメで撮ったのが下の写真である。まずはこの「写真をじっくりと眺めて」みて欲しい。
 |
私が感じた「雄大な景色」は伝わっただろうか? きっと私の感じた「雄大な」感じは百分の一も感じられないに違いない。それでは、次に片目をつむって、もう片方の開いた目だけでこの写真をもう一度眺めてみてもらいたい。そうすると、今度は一体どんな風に感じられるだろうか?今度は、立体的に浮かび上がる山と谷が浮かび上がってくるハズである。
この「片目で写真を眺める」というのは南伸坊の「モンガイカンの美術館」の中で書かれている「写真の見方」である。その一部分を引用してみると、
ヒトの視覚の特殊性というのは、横に並んだ二つの目が、それぞれ違った映像を感じて、それが脳ミソでかきまぜられて、立体を感じるようになっていることなのだった。私はこれを初めて読んだときは、目からウロコが落ちたような気持ちになった。それまでは、私は写真を「じっくりと眺め」ようとして、両目でじっくりと眺めてしまっていたのである。両目、すなわち、作者とは異なる視点からじっくりと眺めてしまっていたのである。写真に切り取られている景色は作者の視点・場所から描かれているのだから、その場所からじっくり眺めてみれば、もっとそこに切り取られている世界を感じることができたに違いないのだが、そこをちょっと勘違いしていたわけだ。一方、カメラというのは、もともとが片目で見た映像なのである。ファインダーをのぞいていないほうの目を、カメラマンがあけたままであっても、写ってきた写真は片目の映像には違いない。これを両目で見れば、「写真は立体を平面に置き換えたものである」という正論が見えてしまうばかりである。だから、写真を、実物からうける視覚の印象と同じように見ようとするなら、片目で見なければいけないのである。
映画のセットは撮影しているカメラの位置から見るのが正しいのであって、それ以外の位置から見ても意味がない。違う角度から見てみても、それはあまり面白くないのである。いや、もちろん映画村とかユニバーサルスタジオとかそんなのも繁盛しているくらいだから、実は裏側から見るのも面白いのだろうが、それはあくまで表から見終わった後での、「裏の眺め」なわけだ。
そういったわけで、写真を眺めるときには「(作者と同じ)片目でじっと眺める」のが良いわけであるが、それは写真だけに限らない。平面に描かれたものであればそれは何だって同じである。普通の絵画だって、版画だって、もう何でもそうだ。例えば、このモネの「散歩、日傘をさす女」を両目と片目で眺めてみよう。これはモネが家族を光り輝く景色の中で描いた名画である。
 |
両目でじっくり眺めてしまうと、いまひとつ感じられない風の感じや空気の透明感が、片目で眺めると躍動感と共にあなたの目の前に迫ってくることと思う。片目でこの画を眺めるとき、私達の目はセザンヌが「彼(モネ)は眼である。しかし、何という眼だろう。」と評したモネの目と一体化し、モネが眺めた景色を私達も眺めることができるのだ。
というわけで、写真に限らず平面に描かれたものであれば、私は片目で作者と同じ視点に立って眺めてみるのが面白いと思うわけだ。平面に描かれた写真や絵画には、作者の片方の目から見た視点しか描かれていないので、私達も同じように片目で見てやればあとは私達の想像力が作者のもう片方の視点を作りだし、作者の感じた世界を立体的に感じることができるのである。
と、そんなことを新穂高ロープウェイスキー場のリフトの上でぼぅ〜と考えていると、少し面白いことを思いついた。平面に描かれた写真や絵画には、作者の片方の目から見た視点しか描かれていないのであれば、もう一つの視点を想像して、そのもうひとつの視点から眺めた情報を絵画に加えてしまえば良いのである。
簡単に言えば、オリジナルの画に描かれている物体の距離に応じて、左右の視差をつくってやった二枚の画像を作れば良いのである。そして、その二枚の画像を左右の目で眺めてみれば、作者が同じく左右の目で眺めている景色、作者が描こうとしたものを眺めることができるかもしれない、と思ったのだ。もちろん、その処理にはいくつかの面倒なこともあるのだが、その処理の細かい内容・注意についてはまた次回以降に説明してみることにして、今回はまずはそういう処理をしてみた名画を見ていくことにしよう。
というわけで、これが作者の視点情報を勝手に加えて3D化したモネの「散歩、日傘をさす女」hirax.netEdittionである。この二枚の画像を平行法、つまり右の絵を右の目で眺めて、左の絵を左の目で眺めてみたならば、キャンバスの中で佇んでいる妻カミール・モネと息子ジーンが、キャンバスの中から浮かび上がってくるはずだ。その時、二人の背景の青い空もより深く見え、空気の透明感も流れる風が流れる時間と共に浮かび上がってくるのである。
 |  |
このThe Stroll, Camille Monet and Her Son Jean hirax.net Edittionを眺めれば、あなたもモネの視点から、彼の両目に映るカミール・モネを感じることができたことと思う。平行視が苦手な人は目の力を抜いて、ゆっくり挑戦してみてもらいた。平行法のコツはぼぅ〜と遠くを眺めるように、目の力を抜くことである。
この「散歩、日傘をさす女」は単に紙で作ったニセモノのパノラマの景色みたいに見える、という人がいるかもしれないので、次にシャガールの「窓」も同じように眺めてみよう。まずは、オリジナルの「窓」である。
 |
そして次が、作者の視点情報を勝手に加えて3D化してみたシャガールの「窓」hirax.netEdittionである。これも同じく、平行法で描かれている。シャガールが眺めている窓の向こうの景色、世界が深い奥行きと共に目の前に出現するハズである。
 |  |
さて、写真にせよ絵画にせよそれは作者の視点から世界を切り取ったものである。その「切り取る」という作業は、このシャガールの絵のタイトルではないが、"window"=「窓」そのものである。限られた「窓」によって画家の感じた世界の一部がカンバスの上に切り取られる。それは逆に言えば、カンバス上に画家の感じた世界へ開かれた「窓」が開いている、ということでもある。
もちろん、私達の視点は必ずしも作者の視点とは同じでないし、作者が世界を切り取った窓もごく限られた小さな窓だろう。だから、なかなか作者が感じた世界を共有することはできないだろう。しかし、作者の視点を想像しながら、作者の切り取ったごく限られた窓に立って外を眺めてみる時、きっとそこには描かれている世界は生き生きと見えてくるに違いないと思うのである。
2001-02-11[n年前へ]
■もう一つの目から眺めた世界 
hirax.net式「平面画像立体化法」
先日、出張のついでに本屋で野田秀樹の「20世紀最後の戯曲集」を買った。電車の中で冒頭の「RightEye」を読んでいると、こんな台詞があった。
オレはもう二度と、立体写真を見ることができない。立体星座早見盤とか、アトラス立体地図とか、ああいうのが見れなくなるんだぞ。「Right Eye」は野田秀樹自身の右目失明、カンボジアで亡くなったカメラマン一ノ瀬泰造、被写体を執拗に追いかけるパパラッチ達、そして死んでいった一人の女性が姿形を変えながら絡み合っていく話だ。
立体写真を見ても立体感を感じるかどうかは人それぞれであるし、空にかかる虹を眺めてみてもそれが何色に見えるかはやはり人それぞれだろう。「平面画像を立体化する話」の話を書いてみても、それを眺めることができない人もいるし、Photoshopを使った話を書いてもPhotoshopを持っていない人には面白くないだけかもしれない、そしてオッパイ星人の話を書けば(いつもバストを大きくしがちなのは、わかりやすさの都合上だったりするだけなのだが)、それで不快になる方も多々いることだろう。
それでも、今回も立体画像の話、「平面画像立体化」の続きを書く。
さて、こんな平面画像があったとしたら、どのようにしてやれば立体化することができるだろうか?
 |
人間が立体感を感じる大きな手がかりの一つが両眼視差だ。遠くにあるものを眺める時には、右目と左目にはほぼ同じように見えるが、近くにあるものを見る時は右目と左目の場所が違うため、右目と左目では違う景色が見えることになる。例えば、下の図のように緑色の○が遠くにあって、青色の□が近くにあった場合を考えると、緑色の○は右目からも左目からも同じように見えるが、青色の□は左目からは視界の右側に見えるし、右目からは視界の左側に見える。
|
この左目と右目からの見え方の違いを頼りにして、立体感を得るのが両眼視差である。であれば、左目用と右目用に別々の画像を用意してやり、その位置のズレを意図的に作ってやれば立体的に見ることができるわけだ。
例えば、下の画像のように青色の□を右へずらしてやり、これを左目用の画像に使えば、立体感を得ることができる。
 |
下の画像はそのようにしてやることで、一番最初に示した図を立体的に見えるようにしたものである。この図は平行法= 「左目で左図を見て、右目で右図を見る」なので、遠くをぼう〜っと眺めるつもりでこの図を眺めれば、きっと青い□が近づいて見えて、この図が立体的に見えるようになるハズだ。
 |
こういった方を用いれば、立体画像を作ることができるわけで、実際「立体星座早見盤」というようなものはそういうやり方で作成されているわけではある。
だが、実は一般的に「平面画像を立体化しよう」とすると、話はそう簡単ではない。それは、こんな図を立体化しようとする場合を考えてみればわかると思う。
 |
「さっきと同じで、青い□の位置をズラしてやれば良いんじゃないの?」と簡単に言う人は少しばかり考えが足りない人である。ちょっとでも考えてみさえすれば、大きな問題に気付くハズである。この図のように背景がある場合には、青い□の位置をズラしたら、そのズレた部分は一体どうしてやれば良いのだろうか?
 |
この部分に何があるかは判らない。だとしたら、単純に青い□の位置をズラすわけにはいかない。考えてみれば、そもそも一つの目から見た情報しかないのだから当たり前なのである。もう一つの目から見た時の情報は我々の手元には無いのである。そこの部分をどうしたら良いかは我々にはわからないのである。
しかし、そうは言っても立体化するためにはこの青い□の位置を左へズラしたい。だけど、位置をズラしたらその部分が真っ白になってしまう。だけど、やっぱり立体化したいからズラしたい。"Toshift it or not to shift it; that is the question."というわけで、これはもうハムレットの心境のようになってしまう。このジレンマを解決してやらなければ、背景がある、あるいは距離の異なる物体が視野の中で重なっている平面画像を立体化することはできないのである。
そこで、「できるかな?」ではそのジレンマを解決するために、単に位置をズラすのではなくて、青い□を拡大しつつ位置をズラすというやり方を考えてみたのである。名付けて、hirax.net式「平面画像立体化法」だ。
例えば、上の画像の場合だとまずは青い□を拡大して、その後右へズラすのである。
 |
上の絵を見ればわかるだろうが、青い□を拡大してやると、元の図形と重心は同じだが、その周りに青い□が拡大することになる。そこで、その拡大した分だけであれば、位置をずらしてやっても背景の画像情報が無い場所が露出してしまう、ということがなくなる。このhirax.net式「平面画像立体化法」はつまり、隠された部分が部分的に露出してしまうのを防ぐために、それ以外の部分を隠してしまうというテクニックなのである。
そのようにして、先の一枚の平面画像を立体化すると下の図のようになる。
 |
前回作成したシャガールの「窓」hirax.net版などはそのようにして作成したものである。この画像の場合は窓枠部分は全く同じなのであるが、窓の中の景色を拡大後、左右の目用の画像をそれぞれ左右にズラしている(ズラし量は高さによって変えている。すなわち景色の中で遠くの部分と近く区の部分ではズラし量を変えている)のである。だから、よくこれらの画像を眺めてみれば、景色部分はオリジナルよりもhirax.net版は大きくなっているし、絵の中に描かれている情報自体もむしろ減少していることがわかると思う。
  |
 |
まずは、hirax.net式「平面画像立体化法」の原理がこの「画像の一部を拡大してからズラす」ということなのである。このやり方でシャガールの「窓」のような絵は立体化してやることができる。
しかし、多くの人が気付くと思うがこれだけではまだまだ不十分なのである。最初の例えのように、四角や丸の形状の物体だけがある場合などはこれで十分なのだが、一般的にはさらなる問題が発生するのである。シャガールの「窓」の場合には、窓枠がほぼ四角と丸の組合わさったような形状をしているために、その問題は発生しないのであるが、一般的な形状の場合には話はそう簡単にはいかないのである。そんな場合、すなわち四角や丸の形状の物体だけで画像が構成されていない場合には、どんな問題が発生し、それをどんな風に解決していくことができるか、については次回以降に考えてみることにしたい。
さて、冒頭で読んでいた「Right Eye」の中の「立体写真を見ることができない」という台詞はこんな感じのカメラマンに対する台詞で続けられていく。
この写真を撮った奴らは、右目(Right Eye)をなくしてる。立体感がない。正しい(=right)右目と、覗きたい左目とのバランスを失っている。物を捉える立体感をなくしたままだ。この台詞を眺めていると、前回の話を読んだ人であれば、その中で引用した南伸坊の「モンガイカンの美術館」の中で書かれている「写真の見方」の文章をきっと思い出すことだろう。
一方、カメラというのは、もともとが片目で見た映像なのである。ファインダーを覗いてないほうの目を、カメラマンがあけたままであっても、写ってきた写真は片目の映像には違いない。つまり、立体感を失った平面画像を眺めるときには、カメラマンあるいは画家と同じように覗きたい片目だけで覗かなければならないのであった。そして、その平面画像に奥行きを与えもう一度立体画像にしてやるためには、hirax.net式「平面画像立体化法」ではないが、違う場所から眺めたときに「姿を現してくる隠されたもの」についてどう対応するかということを考えてやらなければならないと思うのである。
これを両目で見れば、「写真は立体を平面に置き換えたものである」という正論が見えてしまうばかりである。だから、写真を、実物からうける視覚の印象と同じように見ようとするなら、片目で見なければいけないのである。
それは、片目で平面画像を眺めて、そして頭の中でその立体感を与える作業をしてやっても良いかもしれない。また、両目を開けて考えてみても良いかもしれない。ただ、ファインダーを覗いてないほうの目で景色を眺めようとする時には、見えていない景色を想像したり、考えたりする必要があると思うのである。その想像力は、ある意味義務でもあるし、また貴重な自由でもあるのかもしれないなと、電車の中で、ドアに寄りかかりつつ「RightEye」の最後の台詞
のこされた(=left)ものは、のこされた瞳(left eye)で、のこされた夢を見続ける義務がある、… いや自由があるを眺めながら、そんなことを考えてみたりした。
2001-09-25[n年前へ]
■純愛で世界を描ききれ 
Study of the Regular Division of the Plane with Innocent Love
先日、出張先で話をしようとした途端、いきなりこんなコトを言われた。
「最近、更新頻度が下がってますねぇ、あとアッチ系のネタが多いですねぇ。」また別の人には、
「たかが風圧がオッパイに思えるものでしょうか?自分には、そこがなんとも不思議で納得できないのであります。」などと言われた。本来、私は真面目な話をしに行ったハズなのであるが、思わず弁解したくなって、
「一体、指の何処でその感触を感じると思われますか?」
「それに、モンローウォークの動画はまるで全裸みたいに見えて、思わず自分はウィンドーを閉じてしまったのであります。」
「いや、掌の広げ方次第で、空気が指に与える圧力が動的に変化するのだが、その指の動きに応じて動的に弾力が変化するさまがアノ感触に近いという想像は如何なものだろうか?たかが風圧、されど風圧、と謙虚に考えるべきではないだろうか?」とか
「空気流が指の側面を押す力が主たる個所だろう、それすなわち、指の周りからこぼれるおちるアレが指に与える感覚なのである。」とか、
「実はOLスーツ編の動画も作成したのだが、そっちの方が私的にはイヤラシク倫理的にNGだったのだ。」とか色々言ってしまったのである。しかし、実はその話をしている仕事場には他にも人が何人もいて、しかもその人達には私は面識は無い。ということは、私は他人の仕事場にイキナリ来たと思ったら、「アノ感触」とか「OLスーツ」とかそんなことを話し出すトンデモない奴にしか見えないのである。これはちょっといけない。いや、かなりマズイ。
そこで、そんなことを言われないために、今回は「できるかな?」のスタート地点である「画像」の話題を考えてみたい。しかも、ただ考えるだけではつまらないので、「できるかな?」風に「愛」を込めて「画像」について考えてみたい、と思う。というわけで、今回は題して「純愛で世界を描ききれ」である。
八月に台風が関東地方を直撃した日、私は東京タワーのすぐ横で「高画質化のための画像処理技術」という研究会を聴講していた。会場に辿り付くまでの間ひどい雨と風に襲われて、最初のうちは「こ・これは、風速25m/s位はあるな。ってことは25mx 3600 s /1000mで時速90kmか…ってことは、計算によればE〜Fカップが今まさに体中にぶつかってきているのかぁ!」なんて(自分を元気づけるために)考えていたのだけれど、風だけでなくて雨もひどかったので、ついには濡れねずみになってしまい、ただ「………」と何も考えずとぼとぼ歩くだけのゾンビ状態になってしまった。
何はともあれ、そんな感じでやっとのこと会場に辿り付いて、いくつかの話を聞いていたのだけれど、その中でもとても面白かったのが、大日本印刷の阿部淑人氏の「シミュレーテッド・アニーリングによるディザマトリックスの最適化」という話だった。色々な項目を適当に重み付けしながら、ハーフトーンパターンを自動で生成して、理想のハーフトーンパターンを作成しよう、というものである。その話の後半では、工芸的なスクリーンの話も俎上に上がり、M.C.Escherの"Sky& Water I"をグラデーションの例に挙げてみたり(残念ながら実際にそんなハーフトーニングをしたわけではないが)、菩薩像を般若心経でハーフトン処理してみせたり、となかなか「できるかな?」心をくすぐるものだった。そこで、私も似たようなことにチャレンジしてみて、さらにはM.C.Escherの版画を使ったハーフトーニングを行ってみたいと思うのである。
 |
そもそも、ハーフトーニングとは多値階調を持つ画像などをニ値出力の(もしくは少ない階調しか持たない)機器で出力するために、多値の階調をニ値(もしくは少ない階調)の面積比率で置き換えることにより出力する方法のことである。例えば、下の例はグレイスケールのグラデーションパターンを円スクリーンによりハーフトーニングしたものである。
 上を円スクリーンによりハーフトーニングしたもの  |
Photoshopを使っている場合には、簡単に任意形状のハーフトーニングを行うことができる。例えば、こんなパターン![]() をカスタムパターンとして登録すると、そのパターンとの明暗比較を行うことにより、
をカスタムパターンとして登録すると、そのパターンとの明暗比較を行うことにより、
という風にニ値化ハーフトーニングを行うことができる。ところが、じゃぁこれと同じようにEscherの版画を使ってハーフトーニングしようと思っても、そう簡単にできるわけではない。なぜなら、このハーフトーニングが明暗比較によって行う以上、ハーフトーニングに使うパターンは多値の画像でなければならないのである。
Escherの版画も版画という(例えば白か黒かといった)ニ値の出力機器を用いているため、やはりニ値の画像に過ぎない。例えば、下の版画はEscherの”Studyof the Regular Division of the Plane with Horsemen”である。
 |
上の版画の一部を(ちょっとだけ細工をしつつ)抜き出してみたのが下の画像だが、白黒半分づつのニ値画像であることがわかるだろう。また、きれいな繰り返しパターンになっていて、平面にこのパターンできれいに埋め尽くすことができるのがわかるだろう。
 |
この画像をPhotoshopのカスタムパターンを用いて、グレイスケールをニ値化ハーフトーニングすると、この画像がニ値画像であるため、下のように階調をきれいに出力することができず、結局のところ「黒か白か」といった階調飛びの画像になってしまうのである。
 |  |
そこで、まずはニ値の画像を元に多値のハーフトーン用パターンを作成するプログラムを作成してみた。作成するやり方としては、初期値を元にして暗い方。明るい方それぞれの方向にローパスフィルターで演算をしつつ、256階調分のハーフトーンを作成し、さらにそれをPhotoshopで処理できるように多値画像として出力することができるようにしてみた。先の発表のやり方で言えば、「高周波を減らす」という項目に重みをおいて、ハーフトーンパターンを自動生成するアプリケーションを作成してみたわけだ(バグ満載状態で)。説明は一切無し、しかもボタンを押す順番を間違えると上手く動かないという状態ではあるが、一応ここにおいておく。名前はhiraxtone.exeでバージョンは0.0…01という感じである。(白黒ニ値だけど24bitモードの)Bitmapファイルを読み込んで、多値のスクリーンを生成するようにしてある。
それでは、このhiraxtoneを用いて、ニ値画像を元に作成した多値階調ハーフトーンパターンの一例を次に示してみる。これは、先の"Studyof the Regular Division of the Plane with Horsemen"の一部分を縮小したニ値画像をもとにして処理してみたものである。 |  |
でもって、上で作成した多値階調ハーフトーンパターンを用いて、グラデーションパターンをハーフトーニングしてみた例が下の画像である。「単純にパターンニ値化した場合」と違って、「hiraxtone1で作成したパターンを使用した場合」はグラデーションが保持されているのがわかると思う。また、階調が保持されているというだけではなくて、まるでEscherのオリジナルの"Studyof the Regular Division of the Plane with Horsemen"のようなパターンにできあがっていることも判ると思う。
 |  |  |
さて、ニ値画像パターンを利用してハーフトーニングすることができる、となると他にも色々と遊ぶことができる。例えば、自分だけのハーフトーンパターンを作ってみたくなることだろう。そして、さらにはその素晴らしいスクリーンに自分の名前を付けて広めてやりたい、と思うのは至極当然の話である。古くはBayerなどがそうしたように、自分が作ったスクリーンに自分の名前をつけてみるわけだ。
とはいえ、私が仮にスクリーンを作成してみたところで、そのスクリーンを私の名前で呼んでくれる保証はどこにもないのである。そこで、卑怯な手ではあるが、自分の名前を元画像にしてスクリーンを作成してみることにした。こうすれば、否でも応でもこのスクリーン形状を呼ぶために人は私の名前を使うことになるわけだ。
というわけで、私の名前「純」という漢字を元データにして、ハーフトーンスクリーン「純」を作成してみた。また、「純」とくれば当然もうひとつ「愛スクリーン」もさらに作ってみた。いや、別に「純愛」を目指そう、と気負っているわけではなくて、単にうちの兄弟は長男が「純」で長女が「愛」なのである。いや、少し気恥ずかしいけど、ホントの話そうなのだからしょうがない。
さて、作成した「純・愛スクリーン」さえあれば、「純愛」で世界を描ききることができるわけで、早速描いてみたのが、下の仲間由紀恵である。オマエの世界イコール仲間由紀恵か?とか、ソレってホントに「純愛」か?とか、つまらないツッコミを入れられそうな気もするが、そんなことはどうでも良いのだ。私はTRICK以来仲間由紀恵のファンになってしまったのだから、しょうがないのである。そしてまた、「純愛」を馬鹿にしてはイケナイ、と私は少しばかり思うわけなのである。(私の名前だから)
 |  |
上の二枚をじっくり眺めてみると、結構キレイに仲間由紀恵が描かれていることが判ると思う。しかも、他でもないこの二枚の画像において、私は「純愛」で仲間由紀恵を描ききっているのである。これより、「純」で「愛」な仲間由紀恵はそうそういないハズなのだ。きっと、本物の仲間由紀恵が見たら「何てピュア〜でラブリーな私かしら。きっと、これを描いた人は心のキレイな人なのね!」と感激すること間違いなし、なのだ。
ちなみに、「純愛スクリーン」でハーフトーニングした仲間由紀恵の左眼の部分を拡大してみたのが下の二枚の画像である。瞳の奥にも、「純」と「愛」が溢れていることが判るハズである。それは言い換えれば、この仲間由紀恵の瞳は「純」イコール「私」で満ち溢れ、さらにはその瞳は「愛」で満ち溢れているのである。
(目の部分の拡大図) 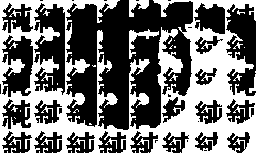 | (目の部分の拡大図)  |
う〜ん、正直ちょっとムナシイけれど、だけどちょっと気持ちが良いのもまた事実なのである。やはり、「純・愛スクリーン」で描かれる世界はとても素晴らしい世界なのである。そうなのである。
さて、今回作成したhiraxtoneは、実際のところ自分でも言うのもなんだが、本当のところ今ひとつキレイな出力ができないし、大体思ったように動いてくれないのである。低周波優先として重み付けをしたハズなのに、どうもそんな風に動いていないし、計算にも時間がかかりすぎる。全てはビールを飲みながら行き当たりばったりにプログラミングするところがいけないのかもしれないが、どうも今ひとつなのである。また、本来であればもう少し元データの形状を残すことを優先(それは高周波優先にならざるをえないだろう)にするようなオプションもつけてみたいのである。
が、とはいえ今回はいい加減思いページになってきたこともあるし、ちょっと疲れてきたこともあるし、とりあえず「純愛」で世界を描ききったところまでで今回は終りにして、続きは次回以降に遊んでみたいのである。

