1999-07-08[n年前へ]
■走査線の狭間 
1/60秒の世界を目指せ
あぁ、今回は(今回も)めちゃくちゃマニアックな話である。トップページには「身近な疑問を調べる」、と書いてあるが、他の人にはぜんぜん身近ではないだろう。最近、妙に忙しいので、身近な疑問がおろそかにされているのだ。身近な疑問の解決は結構難しいのである。そのため小難しい話が続くのだ。困ったことだ。
さて、今回やったことを結論から言えば(*)、AVIファイルをフィールド毎に分解してBitmapファイルに落とすプログラムを作ったのだ。「このソフトはとても便利だ」と言ってくれる人がいたならば、感謝感激雨あられだ。とりあえず、私には欠かすのことのできないソフトである。なぜ、このソフトがそんなに便利なのかを、これから手短に(**)語りたい。
* 「結論から言えば」、とか、「要するに」という人は必ず結論を言わなかったり、全く要約されていない話をするのはなぜだろうか?
** 同じく、「手短に」ときたら、必ず話は長くなる。
一般的なTVで使われている信号はNTSCと呼ばれる。1秒あたり約30フレームからなり、1フレームは2フィールドにわけられる。というと、複雑に聞こえるが実はとても単純だ(***)。単に1フレームが奇数フィールドと偶数フィールドに分かれているだけである。フィールドというとわかりにくいので走査線と考えればわかりやすい、と思う。
*** 当然のごとく、単純ではない。
NTSCの信号を時系列で追うとこのような画像の集合になっている。例えば、こういう具合だ。
1フレーム目の奇数フィールド(走査線)
1フレーム目の偶数フィールド(走査線)
2フレーム目の奇数フィールド(走査線)
2フレーム目の偶数フィールド(走査線)
.
.
.
29フレーム目の奇数フィールド(走査線)
29フレーム目の偶数フィールド(走査線)
30フレーム目の奇数フィールド(走査線)
30フレーム目の偶数フィールド(走査線)
30フレームで約1秒であるから、1枚の画像(フレーム)は約1/30秒である。だから、普通のビデオカメラで撮影した画像は1/30分の1秒毎の画像を示しているのである。しかし、もっと高速度撮影したいと思うときがある。ウン百万出せば、1万分の1秒の撮影でも可能な高速度カメラが買えるが、個人ではとても買えない。また、そもそもやりたい用途向けの高速度撮影用のカメラが存在しない場合というのもままあるのだ。そういった場合には、時間軸に対しては1/30秒までの撮影にしか使うことはできない、と思えるだろう。
しかし、NTSCの信号もフィールド毎に分解すれば、1/30秒の半分、すなわち1/60秒毎の画像を示しているのである。たかだか2倍ではあるが、されど2倍である。1/30秒では見えていなくても、1/60秒では見える世界というのもあるのだ。
画像例を用いて説明しよう。左の1/30秒間の画像を奇数フィールドと偶数フィールドに分解したのが右の画像(a),(b)だ。(a),(b)を比べると、黒い矩形が左から右に移動しているのがわかるだろう。今回のソフトウェアはそういった計測には非常に便利なのだ。このソフトウェアを使えば、普通のビデオカメラの性能を2倍にすることができるのだ。スポーツをやる方などは自分のフォームをチェックするのに使うといいだろう(画像解析までしてフォームチェックはしないか、普通...)。これで、フォームチェックはプロ級だ。
| 1/30のままの例 | 1/60のフィールドに分解した例 |
 |  |
 |
1/30と1/60がたかだか2倍でも結構違うという良い例は、1/30秒のシャッタースピードではブレた写真になってしまう人でも、1/60秒なら大丈夫、とか、ゲームを作る際に1/60秒以内に人間からの入力に対して反応を返してやれば、プレーヤーはスムーズに感じるが、1/30秒ではダメだ、とかいう話がある。
というわけで(****)、AVIで記録された動画ファイルを1/60毎の画像に分解するプログラムが今回作成したものである。
 |
奇数フィールドと偶数フィールドを分けることにより2枚の画像に分解し、それぞれの画像内で失われたフィールドを単純補間により復元することができる。奇数フィールドが先頭か、あるいは、偶数フィールドが先頭かは選ぶことができるし(奇数フィールドと偶数フィールドのどちらが先か選べるということでもわかるように、どちらが先であるか必ずしも決まっているわけではないらしい。そこらへんは、各映像機器によって変えなければならない。)、インターレースでなくノンインターレースの場合、つまり、単にAVIファイルの各画像を静止画におとすことだけもできる。
**** 「というわけで」は話を強引に次へつなげるときに使う。
このプログラムを使ったあとはScion ImagePCを使うのがお勧めだ。Macintoshの世界で一般的なNH-imageのWindows版である。今回のプログラムで作成した静止画群をスタック化して使うのがいいと思う。そうそう、Scion ImagePCに読む込むときには静止画を8bit(gray)画像へと前処理しておくことがお勧めだ。
2000-02-19[n年前へ]
■携帯電話の同時性? 
競馬の写真判定とパノラマ写真 その後
先日
を書いてから面白いメールを頂いた。その一部を抜粋すると、小生は超音波を利用した新しい流体場測定を行っていますが、この方法で得られるDataは空間1次元時間1次元の2次元データです。従って得られるのは、このページにあったような画像が直接得られるわけです。とある。この方法といくつかの結果を発表してから、あちこちからコンタクトがありましたが、その中の一つが、NYのSirovichという高名な流体力学者からの手紙でした。彼はいわゆるSnapShotを、逆に小生のデータから構築できないか、というのです。
今このWebでされたことの逆をしたいというわけです。流れの空間構造を解析するために使いたいのです。残念ながらこれは、以下に少々説明するように、原理的に無理な話で断らざるをえませんでした。
つまり、時間軸に速度をかけて空間軸に変換できればよいのですが、流体場はそれ自身が速度分布を持っていますから、一体何を使えば良いのかが定まらない。
電磁波の場合には光速が一定ですから、時間情報から空間情報を得ることができますが、古典流体力学では不可能なのです。工学的には平均流速を使って、時間-空間の変換をしますが、それはインチキとまでは言わないまでも、便宜的なも
のでしかありません。このWEBの中での例では、馬?の速度のみであとは静止しているので、可能でし
ょう。
「馬?」という箇所に、私との意見の相違があるようだ。私が明らかに「馬」であると言い張っているものに疑問を持たれているような気がするのであるが、今回そこは気にしないでおく。
なるほど、音波や電磁波などを使って計測を行い、得られた
- 空間(あるいは量)-時間
- 空間(あるいは量)-空間
- 海の中の魚を探知する「魚群探知機」
- 気象状況を計測する「気象レーダー」
- 固体の中の電荷分布を計測する「電荷分布測定装置」
「魚群探知機」は超音波を水中に発信して、その反射波が刻々と帰ってくる様子から、(超音波の速度を用いて、空間位置に変換した後に)障害物(ここでは魚群)の様子を計測するものである。「気象レーダー」も電波を使って同様に雲の分布などを測定する。
「電荷分布測定装置」の場合は、(例えば外部電界を印加し)電荷を持つ個所を振動させてやり、その振動がセンサー部に刻々と伝わってくる様子から(あぁ、なんて大雑把な説明なんだ)、(固体中の弾性波の速度を用いて、空間位置に変換した後に)固体の中にどのように電荷分布が存在しているかを計測するものである。
と、文章だけでは何なので、WEB上から、それらの計測器を用いた場合の計測例を示してみる。
下が魚群探知機である。リンク先は
である。 |
また、この下は空間電荷測定装置である。これなども、とても面白いものだ。リンク先は
である。 |
さて、こういうことを、調べてみるだけではしょうがない。自分でもそういう計測をしてみたい。
そこで、次のような実験をしてみようとした。
- 部屋の中に複数の「音の発信源」を配置する。
- 複数の「音の発信源」から同時に音を発する。
- それをPCで収録する。
- 音声が「音の発信源」からPCに到達するまでの時間を解析する
- 複数の「音の発信源」の位置を計測する。
そこで、安易にも時報を使おうかと考えてしまった。しかも、数があって手軽ということで、携帯電話を使おうとしたのである。
しかし、複数の携帯電話を集めて、117に電話して時報を同時に聞いてみると、とても同時どころではない。てんでばらばらなのである。電話のスピーカーから流れてくる時報のタイミングには結構ズレがあるのである。
携帯電話の間には結構同時性がないのだ。また、固定電話とも比較したが、固定電話よりも時報が速いものもあれば、遅いものもあった。
そこで、複数の携帯電話を聞き比べた結果を以下に示してみたい。この写真中で左の携帯電話ほど時報が先に流れており、右になるほど時報が遅れているのである。一番早い左と、一番遅い右では一秒弱の違いがあった。
 |
また、参考までに、家の固定電話と携帯電話の時報を一緒に聞いたサウンドファイルを示しておく。
この携帯電話は先に示した画像の一番左である。つまり、先の携帯電話群では一番時報が早かったものなのである。しかし、家の電話よりは一秒弱遅かった。ということは、家の固定電話と先の一番遅い携帯電話では時報の時間にして2秒弱の違いがあることになる。 そして、「家の固定電話と携帯電話の時報を一緒に聞いた音の変化」をスペクトログラムにしたものを以下に示す。
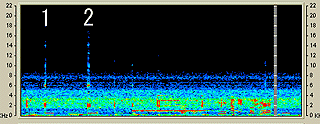 |
水平軸が時間軸であり、時間は左から右へ流れている。また、縦軸は音の周波数を示している。ここでは、「1」で示したのが家の固定電話の時報であり、少し遅れて「2」の携帯電話の時報が聞こえているのが見てとれる。
よく時報を確認することはあるが(実は私はほとんどないのだが...)、携帯電話・PHSで時報を聞く限り、秒の精度はそれほどないようである。また、勤務先の固定電話は先の携帯電話群と比べても遅い方であった。それは少し意外な結果であった。
今回調べた「携帯電話の同時性のなさは」は常識なのかもしれないが、電話の時報で時計を合わせるのはあまり精度が出ないやり方であることがわかっただけでもよしとしよう(別に実験を途中で投げ出した言い訳ではないけれど)。
今度、TV(衛星TVなども遅延時間を考慮した時報の放送を行っていると聞くし)やラジオを用いて当初計画していた実験を行おうと思う。その際には、時報がPCに到達する時間のズレで「音の発信源」までの距離を計測し、左右のマイクでの違いを計測することにより、「立体音感シリーズ」のように「音の方向」を得てみたい。
というわけで、話が「立体音感シリーズ」に繋がったところで、今回は終わりにしようと思う。
2000-05-14[n年前へ]
■恋する心を見てみたい 
恋のきっかけはどの出来事?
まずは、簡単な背景から... 今回の話は
を元に大幅に書き直したものである。少し思うところがあって書き直した結果、まったく別物になってしまった。そこで、ここに登場する次第である。以前の話の場合は、「恋のインパルス応答」という言葉を思いついて、最後におまけのように書いてみたわけであるが、今回はそれをメインに書き直してみたのである。A子:「あのさ、アイツほんと酷い男よ。」
A子:「なんで、あんな男好きになったの?」
B子:「そんなこと言われても、私にだって判るわけないじゃない。」
TVドラマを見ていると、時々こんな会話が流れる。登場人物は二人の女の人、舞台はバーのカウンターや旅先や、とにかく日本全国津々浦々である。そして、話をしている雰囲気は真剣そのものである。きっと、B子は悪い男を好きなっていて苦労しているのだろう。そして、きっとB子の親友であるA子が、悪い男に騙されている「恋する心」で一杯のB子を諭しているところなのだろう。
本当のところ、こんな会話が巷に溢れているのかどうか、私は知らない。そりゃそうだろう。私は男であって、女の人が二人というシチュエーションは全然立ち会える筈がない。じゃあ、同じような会話を私ができるかというと、それもやはりできないのだ。論より証拠、もし私がそんなことを言ったらどうなるだろうか?
私:「あのさ、アイツほんと酷い男だよ。」これは相手が女の人だからで、男なら大丈夫だろう、と言われるかもしれない。しかし、そっちの方が実は質が悪い。
私:「なんで、あんな男好きになったの?」
B子:「そんなこと、何でアンタに言われなきゃならないの?。」
私:「いや、ちょっと…」
私:「あのさ、アイツほんと酷い女だよ。」これはとても危険な会話であることが判るだろう。この後は修羅場が待っているハズだ。あるいは、私は道端に倒れていることになるかもしれない。「小さな親切、大きなお世話」である。根本の原因は私の人間性にあるような気もするのだが、そこは今回は考えないでおきたい。
B男:「なんで、オマエがそんなこと知ってんねん?」
私:「いや、ちょっと…」
さて、最初のB子のセリフ「そんなこと言われても、私にだって判るわけないじゃない。」という会話の真偽はともかく、恋する本人にも恋のきっかけというのは不思議なものなのだろう。そして、本人以外にとっても「恋する心」の揺れ動く様子というものはとても興味深いものだ。
そこで今回は、色々な「出来事・きっかけ」が「恋する心」を変化させていく様子を調べてみることにした。今回の登場人物は、
- A子 : 「瞬間」的に燃え上がるタイプの女の人
- B子 : 「ゆっくり」燃えるタイプの女の人
- C男 : いつも、とっても良い男
- D男 : ほとんどの場合、悪い男
次のグラフは
- 横軸 = 時間軸 左から右へ時間は進んでいるとしておく
- 縦軸 = 「恋する心」の大きさ
 |
「瞬間」タイプの女の人A子の場合、その出来事の前後には「恋する心」が瞬間的に盛り上がる。しかし、それほど持続するわけではないのだ。燃えやすく、忘れっぽいタイプである。芸能人で言うと松田聖子あたりがこの例に当てはまるだろう。
それに対して、「ゆっくり」タイプの女の人であるB子の場合には、「恋の炎」がずいぶんとゆっくり燃え出している。また、「恋する心」の広がりが広い分だけ、「恋する心」の最大値も低くなっている。芸能人で言うと誰になるだあろうか?私にはちょっと思いつかない。
それでは、この 「瞬間」タイプのA子と「ゆっくり」タイプのB子が、いつもとっても良い男であるC男に恋をした場合を考えてみる。まずは、優しいC男は色々なことをするのだ。それが、「恋のきっかけ」となる。
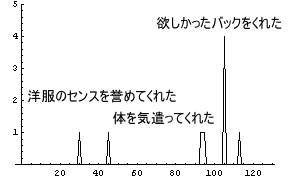 |
時間が左から右へ進んでいくわけであるが、その間にC男は色々なことをするのである。洋服を誉めたり、体を気遣ったり、バックをプレゼントしたり、何ともマメな男である。
また、ここでは「洋服のセンスを誉めたり」、「体を気遣ったり」するという「出来事」よりも、「欲しかったバックをくれた」という「出来事」の方がポイントが高い。ずいぶんと、「即物的」な場合にしてしまった。これなどは、適当にそうしただけで、「私は精神的なポイントの方が高い」という人の方がもちろん私は大好きである。
それでは、これらの色々な「出来事」が起きる時のA子とB子の「恋する心」の変化はどうなるだろうか?先ほど、ある一つの「出来事」に対する「恋する心」の応答を、「恋のインパルス応答」と呼ぶ、と書いた。ある一つの「出来事」によって「恋する心」がどうなるかは、「恋のインパルス応答」を見れば判るわけだ。だったら、色々な出来事が起きた数の分だけ、「恋のインパルス応答」を足し合わせてやれば良いわけだ。この「色々な出来事が起きた数の分だけ、- 恋のインパルス応答 - を足し合わせてやる」という作業を、恋の信号処理では「畳み込み」と呼ぶ。結局、
色々な「出来事・きっかけ」と「恋のインパルス応答」の畳み込み= 「恋する心」という「恋する心」の信号処理が可能なのである。
早速、A子とB子の「恋のインパルス応答」を用いて、先の色々な「出来事・きっかけ」に対する「恋する心」を計算してみた。それが、下のグラフである。黒字がA子、赤字がB子の「恋する心」である。
 |
「瞬間」タイプのA子の場合、ホントに燃え上がるのが早い。C男が洋服のセンスを誉めてくれただけで、もう結構「恋する心」が盛り上がっている。「ビビッ」と恋をして結婚をしてしまいそうなタイプだ。その代わり、一瞬でその「恋する心」が消えているところが怖い。あっという間に離婚をしそうなタイプでもある。
「ゆっくり」タイプのB子の場合は、洋服のセンスを誉められた位では「恋する心」は盛り上がっていない。もちろん、C男に対して良い印象は持ち続けているようだが、恋というほどでもない。
その代わり、A子のように欲しかったバックを貰っても、しばらくすると「恋する心」はすぐに冷める、というようなことはない。C男にとっては、「恋人」になるまでは大変であるが、その後は落ち着いた恋人生活を過ごせそうな相手である。私はC男にはA子よりも、B子の方が相応しいと思うのだが、どうだろうか?(しかし、次回C男には哀しい現実が待ち受けるのであるが...)
さて、このページも少し長くなってきた。そこで、この後は次回に続くことにする。今回、まだ登場していない
- D男 : ほとんどの場合、悪い男
A子:「あのさ、アイツほんと酷い男よ。」という冒頭の会話のような、女の人たちがなぜ数多くいるか(少なくともTVドラマの中では)を明らかにしてみたい。そして、優しいC男の悲しい恋の行方を描いていきたいと思うのである。
A子:「なんで、あんな男好きになったの?」
B子:「そんなこと言われても、私にだって判るわけないじゃない。」
ところで、「辛(つらい)」と「幸(幸せ)」という漢字は互いによく似ている。時々、どっちが「幸せ」だったっけ?と判らなくなりそうになるくらいだ。次回、「恋の印象の平均化効果」というものを武器に、「辛(つらい)」が「幸(幸せ)」にすりかわる様子を見てみることにしたい。「辛(つらい)」が「幸(幸せ)」は紙一重なのだ。「辛(つらい)」は「幸(幸せ)」で、「幸(幸せ)」は「辛(つらい)」なのである。
2001-01-27[n年前へ]
■オッパイ星人の力学 仏の手にも煩悩編 
時速60kmの風はおっぱいと同じ感触か?
本サイトhirax.netは「実験サイト」というジャンルに分類されることが多いようである。何が実験で、何が実験でないのかは私にはよくわからないのだが、とにかく「実験サイト」と呼ばれるサイトは数多くある。そして、その数ある実験サイトの中でも、人間そして愛について日夜取り組んでいるサイトの一つが「性と愛研究所」である。その「性と愛研究所」を読んでいると興味深いことが書いてあった。テレビ番組の「めちゃめちゃイケてる!」の中で何でも「時速60キロの風圧はおっぱいの感触である」と言っていたらしい。そしてまた、「性と愛研究所」では「おっぱいの感触と風圧に関する考察」の中で、「時速60kmでは全然おっぱいの感触ではなくて、ちょうど時速100kmを境に急におっぱいの感触を感じます。」というメールを紹介しながら、
「時速100kmの風では、本物は触れないけどお手軽に疑似体験、名付けて『プリンに醤油でウニ』ではなくなってしまう。それでは、まるで『キャビアにフォアグラでトリュフの味』だ。青少年のために疑似おっぱいを探してあげる必要があるな。」と結論づけている。
この「時速60kmの風」現象は「できるかな?」的にとても興味深いと思われるので、今回じっくりと考えてみることにしてみた。そして、この結論に何らかのプラスαをしてみたいと思う。
そう、前回「オッパイ星人の力学 第四回- バスト曲線方程式 編- (2001.01.13)」でオッパイの表面で働いている力について考えてみたのは、実は単に今回・そしてさらに次回の話のための準備だったのである。(さて、ちなみに今回は会話文体をメインに話が進む。「性と愛研究所」ではないが、この手の話は会話文体の方が書きやすいように思うし、私のバイブル「物理の散歩道」でも「困ったときの会話文体」と言われていたので挑戦してみた次第である。言うまでもないが、AもBも私が書いてはいるが、私自身ではない。)
A : 「東名高速で出勤途中に確認してみたんだが、やはり時速100kmあたりが妥当な感じだったな。」
B : 「何を根拠に妥当なのかがよくわからないが、確かに時速60kmでは手に何かが触っているという感触すらないな。それにしても、哀しい出勤の景色だぞ、それ。」A : 「ほっとけ!だけど、少し考えてみると、このおっぱい(ニセモノ)の感触問題は結構面白く、技術的にもなかなかに深い話だと思うんだよ。」
B : 「はぁそうですか…、としか言いようがないな。」A : 「まぁ、聞け。何しろこのおっぱい(ニセモノ)の感触問題には流体力学のエッセンスがぎっしりと詰まっているんだからな。」
B : 「そんな話は聞いたことはないが、とりあえず聞かせてもらおうか。」A : 「このおっぱい(ニセモノ)の感触問題を解くためには、とりあえず車の窓から手を出したときの指の周りの空気流を計算すれば良いわけだ。」
B : 「ちょっと待て。何で指の周りなんだ。手のひらじゃなくて?」A : 「簡単なことさ。試しにおっぱいを揉む仕草をしてみろよ。」
B : 「こ、こうか?あぁっ?手のひらじゃなくて指で揉んでるっ!」A : 「そうだろ。何故かわからないが、おっぱいを揉む仕草=Mr.マリックが超魔術をかける時のような指使いらしいんだよ。」
B : 「うむ、確かにそのようだな。」A : 「だから、時速60kmの風からおっぱいの感触を受けているのは指先だと考えるのが自然だろ。それなら、とりあえず下の図のような「指の間を抜けていく空気の流れ」を計算してみれば、おっぱい(ニセモノ)の感触問題が解けるわけだ。」
B : 「実写の手に二次元の計算結果を三次元的に合成するという凝った処理が、実にクダラナイことに使われている例だな…」
 | 高速で走る車の窓から手を出して、その手の指の間を抜けていく空気の流れを計算しよう。 鉛直方向の指の等方性を考えて、右の図に示すような指を輪切りにするような水平面のみを考える。 こんな写真を撮るときに、自己嫌悪に陥りがちなのは何故だか知りたい今日この頃。 |
A : 「こういう「空気の流れ」ような流体の力学は、ニュートンのプリンキピアに始まり、オイラーとベルヌーイにより非圧縮・非粘性の理想流体の運動方程式とエネルギー保存則が導かれた。それがオイラーの運動方程式とベルヌーイの式だ。オイラーの運動方程式はちなみにこんな感じだ。」
加速度 = 外力 + 圧力勾配力 v : 速度 |
A : 「基本的には「加速度 = 外力 + 圧力勾配力」という形だな。この非圧縮・非粘性の理想流体の場合はラプラシアンがゼロのポテンシャル流れと呼ばれる単純な流れになる。試しに、そんな場合をNast2Dを元にしたプログラムで計算してみた結果はこんな感じになる。ホントはこの計算自体は完全な理想流体ではないのだが、まぁ大体はこんな感じだ。」
B : 「おっ、あっという間に計算したな。」A : 「まぁ、ポテンシャル流れならエクセルでもちょちょいと計算できるくらいだからな。ちなみに、これは窓から手を出してしばらくしてからの空気の流れだ。」
 |
A : 「で、どうだ?」
B : 「いや、どうだ、と言われても困るが、なんかキレイだな。だけどちょっと小さくて見にくいなぁ。」A : 「そう言われれば確かにそうだ。じゃぁ拡大してみるか。」
 |
B : 「で、この結果から何がわかるんだ?」A : 「この図で空気は左から右へ流れているわけだが、左端の空気の速度と右端の空気の速度は、実は同じなんだ。」
B : 「そう言われても、よくわからないが?」A : 「指を通り過ぎてく空気は、指をとおる前後で運動量がそのまま変わってないってことさ。つまり、空気は指を通り過ぎる時になんら抵抗を受けてないってことだ。」
B : 「えっ?おかしいじゃないか、それなら逆に言えば指も空気から何の抵抗を受けないってことか?」A : 「そういうことだ。これがダランベールのパラドックスだ。」
B : 「じゃぁ、何か?この指先に感じるまぎれもないおっぱいの感触は幻だとでもいうのか!? そんなのオレは認めないぞ!」A : 「まぎれもない、っていうほどのものでもないし、ニセモノおっぱい自体は何か一種の幻のような気もするが、もちろん感触自体は幻であるハズはない。そもそも、空気をサラサラな理想流体として取り扱ったところが間違っているわけだ。そこで、登場するのがナヴィエとストークスだ。彼らはオイラーの運動方程式に粘性を導入した。全てはおっぱいの感触を説明するために、だ。」
B : 「それウソだろ。ナヴィエとストークスが聞いたら怒るぞ。」
加速度 = 外力 + 圧力勾配力 + 粘性力 v : 速度 |
A : 「見ればすぐわかるだろうが、この非圧縮流体に対するナヴィエ・ストークスの方程式は、最後に粘性項が入っている以外はオイラーの運動方程式と全く同じだ。」
B : 「なるほど。こうしてみると意外に簡単な式だな。」A : 「あぁ、オイラーの運動方程式に粘性項が入っただけだからな。そのせいで計算はちょっと複雑になるが、最近のパソコンならノープロブレムだ。というわけで、粘性を考慮して計算してみた結果が次の図だ。」
 |
B : 「おっ、ちょっと様子が違うな。何か、ジェットエンジンみたいに尾を引いてるぞ。」A : 「そうだろ。指の後ろのl様子がずいぶんと違うだろう。で、これを拡大してみたのが次の図だ。」
 |
B : 「左端の空気の速度はもちろんさっきと同じだが、指の後ろでは空気が渦巻いているし、右端の空気の速度は全然違うな。」A : 「もっとリアルに、窓の外に手を出したときの、指の周りの空気の動きを時間を追って計算してみた計算結果のアニメーションが次の図だ。指の周りに空気が渦巻いていく様子がよくわかるハズだ。」
 | 窓の外に手を出したときの、指の周りの空気の動きを時間を追って計算してみたもの。指の周りに空気が渦巻いていく様子がよくわかる。 メッシュを細かく切ったおかげで、計算結果は1GB弱。なんてこったい。 |
B : 「指が空気の中を走り抜いていく様子がよくわかるな。確かにこれなら、空気の抵抗を受けまくりだな。」A : 「そうだ。空気は指から力を受けるし、逆に、指は空気からしっかりと力を受けるわけだ。」
B : 「なるほど、この計算結果は指先に感じるまぎれもないおっぱいの感触を説明しているわけだな。いい感じじゃないか。流体力学そして粘性項さまさまじゃないか!」A : 「あぁ、それも全てナヴィエとストークスのおかげだ。」
B : 「おやっ?ちょっと待てよ!これでは、ただ現実を説明してみただけで、何の解決にもなってないぞ!時速60kmと時速100kmの風の感触の差を説明しているわけでもないし、青少年のためのもっと安全な擬似おっぱいを提供しているわけでもない!」A : 「いや、それがそういうわけでもない。実はこの先があるんだ。このナヴィエ・ストークスの方程式の解はレイノルズ数という無次元数によって決定されるんだ。今回の場合で言うと、レイノルズ数は「指の直径x 車の速度 / 流体の運動粘性率」という形になる。そして、このレイノルズ数が大きくなるほど渦が延びていくんだ。」
B : 「なるほど、わかってきたぞ。つまりあれだな。時速60kmから時速100kmに速度を上げれば、それに応じてレイノルズ数が大きくなって、空気の渦もおおきくなるし、おっぱいの感触も確実なものになるわけだな。勉強になるな。」A : 「う〜ん、実際には密度の違いの方が大きいんだが、ナヴィエ・ストークスの方程式の理解としてはそれでいいかもな。あと、単にレイノルズ数を大きくしたかったら指を太くする、っていうのでもいいわけだ。」
B : 「そう言われても指の太さはなかなか変えられないしなぁ。」A : 「指サックとか色々手はあると思うが、もっといい方法がある。さっきの式を眺めてみれば流体の運動粘性率が小さくなれば、レイノルズ数は大きくなる。例えば、水の運動粘性率は空気のそれの十五分の一だ。」
B : 「ってことは、水の中だったら、レイノルズ数も大きいし、密度も大きいし、指先に抵抗を受けまくりってことだな。すると、水中で手を動かしてみれば、それは空気中の高速クルージングと同じってことになるな!」A : 「そうさ、風呂の中で手をひとかきすれば良いだけの話さ。何もわざわざ時速100kmの車の窓から手を出す必要はないんだ。実際、風呂の中で確かめてみたけど、なかなかイイ感じだ!」
B : 「時速100kmで走る車の窓から手を出すのに較べれば、風呂の中で手をひとかきすれば良いだけなんて、まさに青少年のためのもっと安全な擬似おっぱいだな!」A : 「あぁ、それも全てナヴィエとストークスのおかげだ。」
B : 「それはもういいっ言ってるだろ。」A : 「ところで、ふと考えてみたことがあるんだ。さっき、指を太くすれば遅い速度でもレイノルズ数が大きくなるって言っただろ。東大寺の大仏なんかかなり指が太いじゃないか。」
B : 「確かに、そうだな。」
A : 「今調べてみると、大仏の掌の長さは256cmだ。つまり普通の人間の10倍くらいある。だったら、指の太さも10倍はあるだろう。ってことは、ほんのそよ風が吹いただけでも、大仏の手にはしっかりとしたおっぱいの感触が感じられているんじゃないのかな?」
B : 「単に手が大きいから空気の抵抗も大きいだけどいう気がしないでもないが、指の長さもでかいしさぞかし超巨乳の感触かもしれんな!そう考えると、あの大仏の手も何か実にイヤラシイ手つきに見えてくるから不思議だな!」A : 「う〜ん、悟りを開いているから、指先のヘンな感触なんかには惑わされないんだとは思うけどな。しかし、案外と仏もそんな煩悩と日夜闘っていたりするのかもしれないなぁ。しかも、その煩悩がホントーにあるのかもよくわからない幻のような擬似おっぱいってところが面白くないか?大仏の指先は二十一世紀の煩悩そのものを暗示しているのかもしれん。仏の手にも煩悩ってところだな!」
B : 「言いたい放題だな、全く。」
さて、今回は「オッパイ星人の力学第四回 - バスト曲線方程式 編- (2001.01.13)」と繋がるところまで話が辿り着かなかった。おっぱいの表面張力、マボロシのような指先の流体力学、そして大仏の煩悩をめぐる大河ドラマは人生そのもののようにまだまだ続くのである。
2002-04-27[n年前へ]
■視線のベクトルは未来に向くの? from 麗美さん 
偶然ですが、4月24日に、NHKで夜中に「BSマンガ夜話」の再放送をやっていて、その中で韓国のマンガ「アイランド」を取り上げて、この「できるかな?」と同じような分析を夏目房之介がやっていました。もちろん夏目氏の場合は「できるかな?」のような理系的・数量的な分析ではなく、ストーリーに則った文学的・文芸的分析だったわけですが、両者とも同じような結論ですね。ということで、人物の配置解析によるストーリー解析は的を射ていると思います。
夏目氏の分析でおもしろかったのは、韓国ではマンガの台詞は当然ハングルだから縦書きではなく横書きになります。そのため、日本のマンガのように右から左に読み進むのではなく、左から右に読む進む。つまり、韓国では左開きなのです。とすると、絵も基本的に左右が逆転されます。右に向いた顔は未来指向・肯定的・明るさを表わし、左に向いた顔は過去回顧・否定的・暗さを表わします。じゃあ、日本のマンガの絵をそのまま左右反転させればいいかといえばそうでもないらしいです。台詞が横書きであることも関係して、視線の動きが単純に左右反転では合致しないわけです。
日本人の未来は左で、韓国人の未来は右なんですね(笑い)
(リンク)
