1999-12-30[n年前へ]
■6502と並列計算とムーアの法則 
人間のクロック&スケールアップ
「物理の散歩道」を読み直していると、とある文章に興味を覚えた。
- 第五物理の散歩道 ロゲルギスト著 岩波新書
「通信を考える」の中の興味を惹かれた部分は「信号の伝わる速度と距離と処理速度の関係」を論じている部分だ。例えば、計算機は処理速度を高めるためには回路の大きさを小さくしなければならないとか、人間の頭脳の働きの速さから集団生活の広がりの限界について論じているのだ。例えば、
- 計算機の演算速度の時間スケール -> ナノ秒 = 10^-9s (クロックで考えると、1GHz)
- 人間の演算速度の時間スケール -> サブ秒 = 10^-1s (クロックで考えると、10Hz)
つまり、通信の速度が光速度であるとして、演算の単位クロックの間に通信が行われなければならないとするならば、計算機の時間・空間スケールと人間の時間・空間スケールは等しいだろう、という推論だ。
そして、さらにロゲルギストの想像は広がり、並列計算についても論じている。
計算機が東京と大阪に離れて置かれていて、通信をしながら作業をするとしたら、人間の場合にはそれと同じ条件というのはどんなものだろうか、と彼らは考える。それは、光の速度で55時間、ちょうど冥王星の軌道直径の5倍程度の空間スケールになる、と論じている。それ以上、離れた場合には演算の過程を共に行うのは無理ではないかというのである。
こういう文章を読んでいると、この文章が作られたのが30年以上前であることを忘れてしまいそうである。この人達の思索の自由さに憧れを感じてしまう。この人達は、頭の中にタイムマシンにでも持っているのだろうか、と感じてしまうのだ。
ところで、私がコンピューターをいじるようになった頃は、Apple][の時代だった。といっても、私はお金があふれていたわけではないので、XXX電子でAplle][のコンパチ基盤を買って組み立てて使っていた。その基盤上の6502は1MHzで動いていた筈だ(あぁ、I/Oの6809派vs6502派の論争が懐かしい!)。
それから20年程たち、CPUのクロックスピードは1GHzを越えようとしている。20年で1000倍である。そして、その集積度は、ムーア(GordonMoore)の法則の「半導体の性能と集積は、18ヶ月ごとに2倍になる」に従っている。
それでは、人間はどうだろうか?人間の脳味噌のクロックがどの程度であるか測定されているかどうか、素人の私にはよくわからない。しかし、WEB上のデータとしては、例えば
- Mayo's Profile( http://www.ceres.dti.ne.jp/~mayo/profile.html )
ロゲルギストの時代、すなわち30年以上前、から現在のMayo's Profileの値がほとんど変わっていないように、人間の演算スピードは変わるようなものではない。それは、そうだろう。ヒトのクロックスピードや集積度といったものは、変えるわけにはいかない。当然である。CPUと違ってプロセスルールを変化させるというような訳にはいかないのだ。
それでは、演算性能を上げようとしたらどうするだろうか?そうなると、並列計算を行うのが自然だろう。単独のCPUの性能を上げるわけに行かなくても、共同作業を行えば、演算性能を上げることができる。
現代はほとんどの作業が共同作業で行われる。また、その共同作業も大人数が関わるようになってきている。それは、どんな業種でも同じだ。一人では、なかなかできないことが多くなっている。
それら共同作業、すなわち並列計算、を行う人達(例えれば並列計算機における各ノード)を増やし、それらの間の情報転送をすばやく行うことが多くの作業(計算)を行うための手順だろう。
そこで、
で用いた- 人口増加( http://www.t3.rim.or.jp/~kabutoya/KABHTML/Yoi/2-1.html )
 |
なるほど、人間界の並列計算機におけるノード数は増加している。そして、各ノード間の通信速度を調べるために、まずは、
- 来て、見て、触って、情報伝達
- ( http://www.f-jhs.fukuoka-edu.ac.jp/3-3/jyoho.html )
西暦 内容これを全部転送速度に直してみる。といっても、よくわからない部分も多いので、私が適当に決めてみる。それでは、その変化を示してみよう。とりあえず、ここ200年位の間のものを考える。
-4000 のろし
-2400 伝書鳩
-2300 馬による伝令制度
1837 モールス電信機
1876 ベグラハム=ベル電話機
1909 グリエルモ=マルコーン無線電話機
1973 Ethernet XeroxPARCで生まれる。(ちなみにEther=エーテル)
1979 DIX規格=10Mbps
1992 FastEthernet=100Mbps
西暦 内容という感じだ。グラフにすると、
1837 モールス電信機 = 2bps
1909 グリエルモ=マルコーン無線電話機=10kbps
1979 DIX規格=10Mbps
1992 FastEthernet=100Mbps
 |
こんな感じである。対数グラフにおいて直線的に情報伝送速度が速くなっている。この関係は結構きれいである。
別に意図してこういう数字にした訳ではないのだが、不思議なことである。
このようにして、人間(ノード)間の転送レートが高くなることにより、先のような人口増加に伴うトラフィック増加をしのぐことができていると考えることもできるかもしれない。そして、人間達の共同作業、すなわち並列計算、を行うだけのバススピードを確保しているのである。
最近、会社組織などで分社化とか事業分割とかの話題をよく耳にする。こういった時に、分割における時間と空間のスケールはよく考える必要があるだろう。分割が有効なのは、ほとんど独立なものを分割する場合のみである。並列計算における領域分割などと同じだ。
共同作業がほとんどなく、結果のみをやりとりすれば良いような場合には分割による効果はあるだろう。その一方で、同じ事業・作業を行っているところが、離れていては作業の効率は上がらない。もし、技術系の会社でそのようなことを行うのであれば、事業や部署を並列化した際の真面目なシミュレーション位は行うべきだろう。いや、別に深い意図はないけど。
こういったことは「新・闘わないプログラマ No.109 時代錯誤」に書かれていることとも少し似ているような気がする。
さて、1999/12/30-2000/1/1は野沢温泉で温泉&スキーである。2000年問題で会社に泊まり込む人も多いが、私はスキー場で泊まり込みである。同時期に野沢温泉に行く人がいるならば、ぜひ一緒に「スキー場の特殊相対性理論」について討論したいと思う(スキー場で)。
2000-04-09[n年前へ]
■心に浮かぶハートマーク 
色覚の時空間特性で遊んでみよう
4月である。「四月物語」の4月である。
で書いたように、私は4月だけは英語の勉強をしたくなるのである(何故なら、全然できないから)。そこで、ここのところ英語の先生のところに足繁く出向いている。その時に、信号機の例題を出されて「青信号」と言おうとして私は"ablue light"と言ってしまった。すると、「青信号は"green"だ -> The run signalis green.」と言われてしまった。しまった、確かにその通りだ。いや、英語でそう表現することに納得という話ではない。英語ではこうだと言われたら、私はそのまま頷くのみである。"Yes,sir"状態である。納得したのは、信号機の「現実の」色の話だ。そう言えば、日本でも信号機は「緑色」だった。試しに、信号機の一例を次に示してみる。 実は人にそう優しくないユーザーインターフェースの一例 |
本当は「緑色」なのに、「何故、青信号と言われていたのだっけ?」と考えながら、帰り道に交差点、「緑」信号をじっと見ていた。すると、「緑」信号は消えて、黄信号になった。しかし、私の目にはその瞬間「赤」信号が見えたのである。
私は夢を見ていたわけでも、予知能力があるわけでもむろんなくて、それは単なる錯覚である。「緑」信号が消えた瞬間に「赤」信号が見える、という錯覚である。
私が見た「赤」信号機の錯覚を実感してもらうために、こんなアニメーションGIFを作ってみた。ソフトをレジストしてないが故の、SGという文字は気にしないでもらいたい。下の画像中央にある黒い点を見つめていて欲しい。すると、緑のハートマークが消えた瞬間から、赤いハートマークがおぼろげに見えるはずである。
|
これは、色覚の時間特性による錯覚の一つである。実際に、赤いハートマークがあるわけではない。私の心の中にだけ、浮かぶハートマークである。
その原因となる色覚の時間特性を示すグラフを以下に挙げる。これは色覚の時間特性を示すグラフの例である。色覚のインパルス応答のようなものである。ある色を見た後には、その色の反対色を感じるということを示している。
 |
このような錯覚というのはとて興味深いものである。視覚という「デバイスの特性」が「目に見えて実感できる」ことが特に面白い。以前、
- 分数階微分に基づく画像特性を考えてみたい-同じ年齢でも大違い-(1999.02.28)
- コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
- ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
さて、先の錯覚は色覚の時間特性によるものだった。それと全く同じような錯覚が、色覚の空間特性から得ることができる。そのような錯覚の一つにこのようなものである。それを下に示してみる。
 |
この有名な画像パターンを見れば、「白い線の交差部が赤く見える」はずだ。
これは、色覚の空間特性によるものである。これを示すグラフの例を以下に示す。この場合もやはり色覚の時間特性のように、ある刺激があるとその周囲に反対の色の影響が表れる。例えば、周りに白が多いと、その部分は黒っぽく見える。赤色の周りは緑がかって見えるのである。逆に緑色のものの周りは赤く見えるのだ。
そして、それをさらに進めると、周囲に赤色が少ない場所は、周りに比べて赤く見えるのである。上の画像で言えば、白の交差部は、赤の刺激が少ないので、赤の刺激を逆に感じるのである(ちょっと説明をはしょりすぎかな)。
 |
今回は、このような色覚の空間特性をシミュレートしてみたい。道具は単純にPhotoshopだ。もう手作業でやってみるのだ。ネコの色覚で遊んだ
の時と同じである。 | これがオリジナル画像。黒背景に白い線で格子模様が描かれている。 |
 | 白い(つまり光刺激が多い領域)からの影響を考える。先に示したグラフのように、光刺激がある箇所と少し離れたところではそれと逆の刺激を受けたような効果がある。 そこで、まずは白い部分からの影響をガウス形状のボカシにより、真似してみる。ある画素から少し離れた所に影響が及ぶのをシミュレートするのである。 |
 | 白い部分からの影響(実際には、比較問題となるので黒い部分からの影響と言っても良いだろうか?)は「白と逆の方向、すなわち黒い方向」に働く。 そこで、上の画像を階調反転させる。すなわち、ある画素から少し離れた所に元の明るさと逆の影響が及ぶことをシミュレートするのである。そしてさらに、階調のカーブを鋭くしてやる。 |
 | 上で計算したものとオリジナルの画像を加算してやる。これが、人間が感じる画像をシミュレートしたものである。 白い格子の交差点部が黒く見えているのがわかると思う。といっても、もともとその部分は黒く見えていたとは思うが。 下に、シミュレート画像とオリジナル画像を並べてみる。 |
 |  |
このようにして、オリジナル画像を見たときに感じる錯覚をシミュレートできたことになる(もどきだけど)。
さて、上では簡単のためにグレイスケールで遊んでみたが、最初に示した赤白の場合のようなカラーの例を示してみる。次に示す四角形の中央部は、右と左ではいずれも右の方が赤っぽく見えるはずである。緑に囲まれた領域は、本来の色に対して、緑と逆の赤色に見えるのである。上に示した白黒格子と全く同じ理屈である。
|
|
|
|
さて、この右下の画像中の赤は通常の「赤」よりもさらに鮮やかな「赤」を実現していることになる。左下のものと同じ赤100%の色であるが、左よりももっと鮮やかに見えている筈だ。右下と比べると、左下の赤は落ち着いた赤色に見えてしまうのではないだろうか?
この右下の赤、すなわち緑に囲まれた赤は、物理的にCRTあるいは液晶(今あなたがこのWEBページを見ているデバイス)などの表現可能領域を越えた、さらに鮮やかな赤色に見えているわけだ。ヒトの視覚のデバイス特性が故に鮮やかに見えることになる。
さて、鮮やかな「赤」と言えば、「ポケモンチェック」によれば、日本民間放送連盟のガイドラインには
- 映像や光の点滅は、原則として1秒間に3回を超える使用を避けるとともに、次の点に留意する。
- 「鮮やかな赤色」の点滅は慎重に扱う。
- 前項1の条件を満たした上で1秒間に3回を超える点滅が必要なときには、5回を限度とし、かつ、画面の輝度変化を20パーセント以下に押さえる。加えて、2秒を超える使用は行わない。
- コントラストの強い画面の反転や、画面の輝度変化が20パーセントを超える急激な場面転換は、原則として1秒間に3回を超えて使用しない。
- 規則的なパターン模様(縞模様、渦巻き模様、同心円模様など)が、画面の大部分を占めることも避ける。
しかし、その「赤」と「緑」パターンが細かくなると、何故だか不快なのだ。色覚の時空間特性を考えると、「赤」と「緑」の細かいパターンというのは、もしかしたら読む際に刺激が強すぎるのではないか、と想像してみたりする。根拠はたいしてないのだけれど。
2000-09-02[n年前へ]
■もうすぐ二歳の「できるかな?」 
初心に帰ってみましょうか?
「できるかな?」が始まったのは二年近く前の秋のことだった。
でも触れたが、当初(実は今も続いているが)は某社内の某サーバー内でこっそりと始めてみたのだった。それから二年あまりでずいぶんと色々な話が増えた。某社サーバー内でしかアップしていない- プリンタドライバーは仮免
- 続 電子写真プロセスを分数階微分で解いてみよう
- 続々 電子写真プロセスを分数階微分で解いてみよう
そして話が増えてきたせいか、自分自身でも「アレッ、あの話はどこにあったけ?」というように迷ってしまうことが多々ある。迷うどころか、最後まで見つからないこともしばしばあるのだ。そして、それは私でもない他の人であればましてやそうだろう。というわけで、
では簡単にそれまでの話の紹介をしたし、ではhirax.net内の全文検索機能を付けてみた。今回は、これまでの話題をもう一度自分で読み直して、その中から「自分のお気に入り」を調べてみたいと思う。そして、最近少し話題が変になってしまっている反省をして、もう一度初心に帰ってみようと思うのだ。
まずは、1998年の話題からいくと
というあたりが、良い感じだ。京都の風物詩である「鴨川カップル」達が人目を気にしながら寄り添う合う姿を考えてみたものだ。後の「恋の力学」シリーズなどはここらへんから始まっていた、といっても良いだろう。そしてこの頃の[Scraps]系の話題としては、がある。少し前に、この「さなえちゃん」を描いた漫画の作者からメールを頂いたのがとても私には印象深かった。そして、1999年の上半期から選んでみると、まずは
というところだろう。ハードディスクの情報を可視化することで情報圧縮・エントロピーを考えてみた一話である。そして、同じような「可視化シリーズ」の一つである- 感温液晶でNotePCの発熱分布を可視化する- 熱いところで感じてみたい St.Valentine 記念 - (1999.02.14)
- NotePCの発熱分布を比べてみたい- お熱いのがお好き SOME LIKE IT HOT - (1999.02.15)
そして、1999年の下半期はもう自分で言うのも何だが傑作揃いである。大体、書いているペースが自分でも驚くくらいのハイペースだ。月当たりの話の数を数えてみると、
- 7月 9話
- 8月 9話
- 9月 8話
- 10月 8話
- 11月 11話
- 12月 9話
この頃の「お薦めの話」はいっぱいある。例えば、
に始まった「文章可視化シリーズ」や、で始まった「ASCIIアートシリーズ」だろう。から始まる「江戸五色不動シリーズ」は江戸にロケまで行ったので、とても思い出深い話の一つである。しかも、妙な偶然のせいでまるで小説の中に迷い込んだような気持ちになったものだ。そして、WEBページを作る上では
などもどうしても外せない。そして、この後結構続くことになるという「恋の力学」シリーズもこの時期に始まっている。そして、この頃の一番人気が何と言ってもだろう。この「ミニスカート」系の話の流れは以降も続くことになるのが自分では意外でもあり、残念でもある。それはさておき、ナンセンス系ではなんてのも面白い話だと思う。そして、1999年の終わりはやはりこれが「お気に入り」の話である。また、[Scraps]系の話がこの時期にはやたらいっぱいあるのが面白いところだ。その内からいくつかピックアップするとこんな感じだろうか?- [Scraps]絵馬 - どこにもいないよ- (1999.07.09)
- 新宿駅は電気羊の夢を見るか- 意識とは何か - (1999.07.10)
- [Scraps]合掌 - キレイはキタナイ、キタナイはキレイ- (1999.08.01)
- [Scraps]いつかきっと -掌の中の答え - (99.11.03)
- 「文学論」と光学系 - 漱石の面白さ-(2000.02.27)
- 恋の力学 恋の相関分析編- 「明暗」の登場人物達の行方 - (2000.04.01)
- 恋の力学 恋のグラフ配置編- 「明暗」の収束を見てみよう - (2000.04.02)
- 恋する心を見てみたい - 恋のきっかけはどの出来事?- (2000.05.14)
- 恋の形を見た人は - 恋の相対性理論- (2000.05.17)
さて、今回は2000年上半期までの話の中から「私の好きな話」を振り返ってみた。とはいえ、私の好きな話=他の人の好きな話ではないようだし、他の話も適当に眺めて頂いたら良いかなぁ(私が)、と思うのだった。
2000-12-24[n年前へ]
■サンタクロースを捜して 
Double Role on Christmas Eve
2001-12-24[n年前へ]
■サンタが街にやってくる 
複数サンタクロースの巡回問題
簡易に書き直した2011年版もあります。
幼い頃、クリスマスの夜を清里の聖ルカ教会で過ごしたことがある。今では、「アイスクリーム」で有名になってしまった聖ルカ診療所の隣の教会だ。清里を通る小海線が蒸気機関車からディーゼル列車に切り替わった頃だった。私の住んでいた野辺山から一番近い病院がその聖ルカ診療所だった。今はどうなのか判らないけれど、あの病院の中の風景はまるで高原の療養所のようで(高原の診療所なのだから大して違いはないのだけれど)、とても不思議だった。
さて、クリスマスの人気者と言えば、やはりサンタクロースである。世界中の子供達から待ち焦がれられ、プレゼントを配って歩くのだから、クリスマスイヴのサンタは大忙しなのである。一体、サンタクロースはどんな風にプレゼントを配って歩くのだろう、と思った私は「サンタクロースの巡回問題」について考察をしてみることにした。
知らない人のために書いておくと、「巡回サンタクロース問題(TSP:TravelingSanta Problem)」というのは「巡回セールスマン問題(TSP:Traveling SalesmanProblem)」の特殊例である。そもそも「巡回セールスマン問題」というのは「n人の顧客の場所が与えられたとき、全ての顧客を一回ずつ経由して巡回する際に、移動距離が最小になる経路を求める。」という問題である。計算幾何分野で最もメジャーな話であって、カーマーカー特許などこれに関係するものである。つまりは、色々なものを配達する際には「配達経路を考えるのは実は結構大変なのだ」という問題なのである。
これまで「巡回サンタクロース問題」を考えた人がいなかったか、と言うとそんなことはなくて、試しにinfoseekで"サンタ"AND"巡回"で検索すると、既に素晴らしい研究がなされている。それが
- サンタクロース研究
- ( http://www.geocities.co.jp/HeartLand-Suzuran/5872/santa.html )
そこで、そんなこれまでの「巡回サンタクロース問題」に関する研究を踏まえながら、「できるかな?」ではさらに「サンタクロース巡回問題」を考え、そして、できることであればサンタの隠された真実にさらに迫ってみようと思う。「サンタクロース巡回問題」の中には、サンタクロースの真実に近づく鍵が含まれている、と私は何故か感じるのである。
まず、始めに問題提起をしてみよう。
「果たしてサンタは一人なのか?」
どのような事件においても(別に事件ではないが)、単独犯か複数犯かというのはとても重要な問題である。犯人が単独犯か複数犯かで証拠の指し示す意味は異なってくる。サンタは一人、と私たちは何故か思い込んでいるが、そんな先入観は正しい捜査のたまには捨てる必要がある。
そこで、まずはサンタの歴史から調べてみると、Santaさんの起源、クリスマスページ!によれば、サンタクロースの起源であるSt.Nicolausは西暦4世紀頃の人であるという。その頃の人口は現在よりもはるかに少なかった。それは、サンタの労働量がはるかに少なかったということだ。なるほど、この時代であれば、サンタは一人でも不思議ではないかもしれない。
とはいえ、Santaさんの起源の中の色々なサンタの目撃情報を見ると、本当にサンタは一人なのか疑問を感じるのもまた確かである。色々なサンタが目撃されている、ということはサンタは実は複数犯の可能性が高いのではないだろうか?
また、世界の人口は人口増加に示されている全世界の人口増加の様子を見れば明らかなように爆発的に増えている。ちなみに、そこに示されているグラフを対数軸にし、近似式を加えたものが以下である。
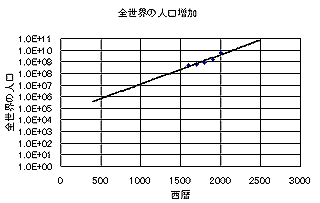 |
St.Nicolausのいた西暦4世紀頃に比べて現在の人口は4桁、すなわち、10000倍に増えている(近似式によれば。ホントのところは知らない)。これでは、サンタクロースは年々仕事量が驚異的に増えていることを意味する。もし、サンタが単独犯であるとするならば、過労死はまぬがれそうにない。
サンタの単独犯説に対する疑問は「サンタクロース巡回問題」からも示される。N人の顧客(今回の例ではN人の良い子供)が与えられたとき、サンタが計算しなければならない経路の総数は(N-1)!/2で与えられる。2で割っているのは「対称巡回サンタクロース問題(A家からB家間での距離と、B家からA家間での距離が同じという性質がある場合)」であるからだ。
子供の家N=100までの場合の、サンタが計算しなければならない経路の総数(N-1)!/2を以下に示してみる。
 |
どうだろうか、Nが少し増えると爆発的にサンタが計算しなければならない経路の総数(N-1)!/2が増えていくのがわかると思う。一軒多くなるだけで、ものスゴイ数の計算をしなければならなくなるのである。サンタが実際に配達して回るのも大変だが、その前に配達経路を決める計算量は実はもっと大変なのである。
先の人口増加の割合をこれに加えるならば、「サンタが計算しなければならない経路の総数」は天文学的数字になることは明白である。
そこで、私はやはりサンタ複数犯説が真実に近いと思うのである。サンタ複数犯説が正しいとするならば、ッ実はこの「サンタクロース巡回問題」は遥かに容易に解くことができるようになるのである。
それでは、複数サンタがいるときの「サンタクロース巡回問題」を考えてみよう。サンタが複数のm人いる場合を考える≠ニA「サンタが計算しなければならない経路の総数」はm*(N/m-1)!/2で示される。
一例として、サンタが1,2,10人の場合を示してみる。
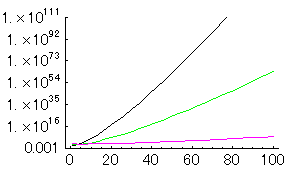 |
このグラフからサンタが複数いる場合と、単独の場合とで巡回経路を考える手間が全然違うのがわかるだろう。サンタが2人いると、計算量は半分になるのではなく、ものすごく少なくなるのである。
実際の巡回においての仕事量は、サンタがm人いれば1/mになる。しかし、その前準備はサンタがm人いれば((N-1)!/2)/(m*(N/m-1)!/2)分の一になるのだ。簡単に言えば、メチャクチャ楽になるのだ。サンタが一人では事実上サンタがプレゼントを配ることは不可能だけれど、複数犯であれば容易にプレゼントを配ることができるのだ。
このように「複数サンタクロース巡回問題」を考えることにより、サンタは複数いることが明らかだと私は思うのだ。
ただこれだけでは、不十分だ。全世界の子供達も年を経るに従って、爆発的に増えている。サンタが複数いるにしても、それでもやはり大変だ。サンタ達の人数も爆発的に増えていかなければ、とてもじゃないがやってられないことだろう。
それを解決する一つの答えはこうだ。「子供が増える割合に従って、サンタも増える」と考えるのだ。子供が一人増えると、サンタも一人増えるのだ。そうすれば、何の問題もない。子供が一人現れると、サンタも一人増えるのであれば何の問題もなくなる。
ところで、「子供が一人現れると、サンタも一人増え、サンタの数が子供と同じ比率で増えていく」ということは、子供たちがいずれサンタになるという考えが自然だとは思えないだろうか。そうだ、子供達がサンタになるのだ。子供達が大人になって、そしてサンタになるのだ。
もしかしたら、それはサンタという名前ではないのかもしれない。普段は他の名前で呼ばれているのかもしれない。けれど、クリスマスだけはサンタという名前になるのだ。電話ボックスで着替えるちょっと情けないスーパーマンのように、クリスマスイヴだけは彼らは変身するのだ。
こうして、サンタ達は子供の枕元にやってくる。むかし子供だったサンタ達が子供達の枕元にやってくる。そして、夢を見ている子供達が起きてしまわないように、そっと枕もとにプレゼントを置く。
サンタなんかこれまで私の枕元には来なかった、という人たちも多いのかもしれない。けれど、きっと、そんな人たちもまたサンタになっていくのだろう、そして、その時、本当にサンタがいる、ということに気づくのだろう。




