1998-01-08[n年前へ]
■Photohoの乱数プラグインを作成する 
「2項分布のムラについて考える」の関連して、Photoshopの乱数プラグインを作成したのでメモしておく。 PhotShopはとても便利なソフトである。画像を取り扱うにはトップクラスと言っても良い。あえて、難を挙げるならば8Bit階調が基本という所である。もちろん、12bit階調なども扱えるのは知っているが、基本機能とは言えないと思う。
しかし、PhotoShopで凝ったことをしようとすると、Pluginを作らざるを得ない。PhotoShopでPluginをつくるには2つのやり方がある。それは、
- Adobe提供のPlugin SftwareDevelopmentKitを使ってPluginを作る。
- FilterFactoryを使ってPluginを作成する。
今回はランダムノイズをつくるためのプラグイン作成が目的である。その程度であれば、FilterFactoryを使うのが簡単で良い。
 | まずは、FilterFactoryを使う。 |
まずは、Redチャンネルにのみ乱数を与えるものをつくる。以下がそのパラメータである。
 | たった、これだけである。 Redに乱数を与え、Green,Blueのチャンネルには0を与える。 |

もうひとつ、各色に乱数を与えるプラグインのサンプル画像はこのようになる。

さて、試しに使ってみる。1000x1000ドットのランダムノイズ画像を作成してみる。その画像はここに載せるには大きすぎる。そのため、その一部を左下に示す。その画像に対して各領域10x10の100ドットで平均し、100x100に変換した画像を右に示す。詳しくは「2項分布を考える」を見て欲しいが、100ドットで平均したくらいではフラットにはならない。それどころか、有限のいくら広い範囲で平均しても正確にはフラットにはならない。もし、フラットになるのであれば、それはランダムな2項分布ではない。もちろん、PhotoShopの丸め誤差とかの話は別にしておく。また、「2項分布を考える」の際は1次元の1成分データであったが、今回は2次元3成分データである。そのため、人間にはよりフラットに見えにくい。相対的な色差に対しては人間の目は敏感だからである。
 |  |
今回の例も「2項分布の特性:どんなに広い領域であっても、領域中の平均が一定でない」の当然の結果である。仮に、ある広い領域中の平均が一定であるような確率過程を用いればこのようなことは生じない。もしも、そのような確率過程に基づくものがあったら、部分部分はランダムに見えても、広い領域ではフラットに見えるのである。
1999-02-28[n年前へ]
■分数階微分の謎 
線形代数、分数階微分、シュレディンガー方程式の三題話
分数階微分?
InterLabの1999No.5を読んでいると面白い記事があった。いわき明星大学理工学部の榊原教授の「Waveletと数式処理ツール」という記事である。といっても、興味を持ったのはWaveletのことではない。もちろん、Waveletに興味がないわけではない。この榊原教授が講師を務めたWavelet講習にも参加したこともある。しかし、今回興味を惹かれたのはその記事中にあった「分数階微分の解析」である。InterLabの榊原教授の記事を引用すると、-通常微分・積分は整数回実行できるが、分数階微分はこれを分数に一般化したものである。さまざまな物理や工学の現象の記述に使われるようになった-とある。一階微分とか二階微分というものはよく使うが、0.5階微分などというものは使ったことがない。どのようなモノなのかさえよくわからない。
参考:
一体、どんな物理や工学の現象の記述に使われているのか知りたくなったので、infoseekで調べてみる。すると、いわき明星大学の清水・榊原研究室の「粘弾性動モデル」が引っ掛かる。
参考:
衝撃吸収・シリコーンの弾性率などに興味を持っている人には面白いかもしれない。もう少し調べてみると「バナッハ空間バナッハスケールにおける分数階積分作用素」というようなキーワードも引っ掛かる。
そこで、まずは勝手に分数階微分について考えてみた。
分数階微分・積分の勝手な想像図
まずは、イメージを考えるためにグラフを作成してみる。x^2の関数、および、それを微分・積分した関数である。微分は3階まで、積分は2階まで行っている。
 |
このグラフ形式の表示をちょっとだけ変えてみる。
 |
ここまでくると、平面グラフにしてみたくなる。つまり、微分・積分の階数を離散的な整数値でなく、連続的な値としてのイメージに変えたくなる。
 |
これで、微分・積分が整数階でない場合のイメージ(勝手な)ができた。微分・積分が離散的なものではなくスムーズにつながっているものであるというイメージである。図.2から図.3への変化をよく覚えていてほしい。
といっても、これは数学的なイメージのみで物理的なイメージはまだここでは持っていない。位置、速度、加速度などの微分・積分で選られるものに対して同じようなイメージを適用すると、位置なんだけれどちょっと加速度っぽいもの、とか、速度と加速度の「合いの子」みたいなものというような感じだろうか?
さらに、これから先は、f(x)という関数が示す無限個の値を位置ベクトルと考えて、f(x)というのは無限次元空間の一つの点だというイメージを持つことにする。線形代数を考えるならそれが一番わかりやすいだろう。任意の階で微分された関数群が集まって、さらに高次元の空間をなしているというイメージである。
分数階微分を調べる
勝手なイメージはここまでにして、手元にある数学の参考書の中から手がかりを探してみた。すると、大学院入試問題解説 - 理学・工学への数学の応用 - 梶原壌二 現代数学社ISBN4-7687-0190-6
の中に手がかりがあった。あれ、ということは以前にやったはずなのか...そう言えばおぼろげな記憶がちょっと...
その中の言葉を少し引くと、
フーリエ変換は等距離作用素である、関数空間L^2(R)における回転といえる。結局、
となる。そして、古典力学におけるハミルトン関数において、運動量を微分演算子で置き換えれば、量子力学や量子化学のハミルトン演算子が得られ、シュレディンガー方程式などにつながるのである、とある。他の資料を眺めてみると、どうやら量子力学などの分野からの要請に応じてここらへんの微分演算子の分野が発展しているようだ。理論物理などをやった方ならよくご存知のことだろう。例えば、水素原子の基底状態の波動関数へ運動エネルギーの演算子を作用させるというような、基本的な所でも、このフーリエ変換を用いた微分演算が用いられてる。ここで、fは元の関数であり、Fはフーリエ変換
さて、この式自体は非常に簡単である。それにイメージも湧きやすい。
i を掛ける演算、私のイメージでは複素数空間の中で90度回転をする(言い換えれば、位相が90度ずれる)演算、が微分・積分であるというイメージはスムーズに受け入れやすい(それが正しいかどうかは知らないが)。なぜなら、微分が空間の中での回転であるとすると、三角関数の微分・積分に関する性質(例えば、Sinを微分するとCosに、Sinを2階微分すると-Sinになる、すなわち、一回の微分につき位相が90°ずつ回転する(位相がずれる)というような性質)が納得でき、それがフーリエ変換という形で登場してくることがスムーズに受け入れられるのである。また、微分といえばとりあえず三角関数の登場というイメージもある。
もう少しわかりやすく書くと、
- 三角関数では一階微分の結果は90度位相がずれる(回転する)。
- ならば、(例えば)0.5階微分は45度位相をずらせば良い。
- 任意の関数もフーリエ変換により、三角関数に分解される。
- ならば、任意の関数に任意の実数値の微分が成立する。
任意の関数をフーリエ変換し三角関数に分解した時の位相、言い換えれば、周波数領域での位相ずらし、で分数階微分が定義されるということは、物理的実用的に大きな意味を持つ。例えば、電磁波、弾塑性運動などの物理現象の中での位相変化を分数階微分で解けることになる。例えば、複素貯蔵弾性率などについて分数階微分との関係は深そうである。あるいは、媒体中の電磁波の位相などについて適用するのも面白そうである。
分数階微分を使ってみる
よく分からないところも多いが、とりあえず、
という式を使ってみる。まずは、使ってみないとわからない。とりあえず、1次元の関数を作成して、この式を適用してみる。まずは、よく出てくるガウス分布で適用してみる。まずはガウス分布とそれの通常の一階微分の解析解を求める。
 |  |
それでは、今回の方法による一階微分の結果と、それと解析解との比較を示す。なお、本来無限領域のフーリエ変換を有限の領域で行っているため、端部近くで変なことが生じるのはしかたがないだろう。また、色々な事情により係数の違いは無視して欲しい。
 |  |
ちょっとずれが生じているが、こんなものだろう。しかし、これだけでは今回のフーリエ変換を用いた微分の面白さはでてこないので、0から2の範囲で連続的に分数階微分をしてみる。
 1/10 (=0.1)階微分 |  1/2 (=0.5)階微分 |  7/10 (=0.7)階微分 |  1階微分 |
 13/10 (=1.3)階微分 |  15/10 (=1.5)階微分 |  17/10 (=1.7)階微分 |  2階微分 |
モーフィングのようで面白い。
さて、今回は分数階微分を勉強してみる所までで、これの応用は別に行ってみたい。もちろん、言うまでもないと思うが、間違いは多々あると思う。いや、田舎に住んでいるもので資料がないんですよ。
1999-03-25[n年前へ]
■電界計算をしてみたい[有限要素法編その1] 
有限と微小のパン
今回のサブタイトルは一目瞭然であるが、森博嗣のミステリのタイトルそのままである。
 |
何故、「電界計算をしてみたい-有限要素法編その1-」が「有限と微小のパン」に繋がるのか。もちろん、"有限要素法"と"有限と微小のパン"の「有限」をかけた駄洒落ではない。有限要素法を考えるとき、私は森博嗣に足を向けては寝ることができない。それが、なぜかは下の本を見ればわかる。
 |
これは、学生時代に有限要素法を勉強するために使った本である。「森 博嗣 著」と書いてあるのがわかるだろうか。いや、まさかこの本の作者がミステリを量産するとは想像もしなかった。ビックリである。講談社ノベルズと森北出版の両方から本を出している人は他にはいそうにない。
本題と関係のない話はここまでにしておく。今回はMathematicaで有限要素法を用いて静電界計算を行いたい。とりあえず、ソルバーとプリ・プロセッサまでつくる。その応用は続きの回で行いたい。Mathematicaで有限要素法を勉強するには、森北出版の依田 潔 著「Mathematicaによる電磁界シミュレーション入門」を参考にした。任意の電荷配置のPoisson方程式を解くようにしてある。
次回に詳しく計算モデルの説明を行うので、今回は計算モデルの詳細については記述しない。Notebook内に、モデルの詳細は記述してある。
このNotebookを使った計算、出力例を以下に示す。
| 平行平板電極の間に誘電体層があるモデル | 平板電極と三角柱電極の間に誘電体層があるモデル | 平板電極と円柱電極の間に誘電体層があるモデル |
 分割要素 |  分割要素 |  分割要素 |
 電位表示(色がきちんとしたhueでないことに注意) |  電位表示(色がきちんとしたhueでないことに注意) |  電位表示(色がきちんとしたhueでないことに注意) |
 半分の領域の電位を鳥瞰図にしたもの |  半分の領域の電位を鳥瞰図にしたもの |  半分の領域の電位を鳥瞰図にしたもの |
Mathematica3.0のHTML出力は大変便利だが、漢字が化けるのが困りものだ。しかも、ちょっと似た漢字に化けてしまうからわかりにくい。今回のNotebook中で化けた漢字を以下に示す。
- 油界 <- 電界
- 堰素 <- 要素
- 誘油 <- 誘電
- 姦み込む <- 組み込む
- 表傭 <- 表面
- 壓さ <- 高さ
- 堆心 <- 重心
- 肖似 <- 近似
- 内占 <- 内部
- 傭積 <- 面積
- 回寂 <- 回転
- 進当 <- 適当
- 懷瞰 <- 鳥瞰
中国語みたいな化け方である。しかも、意味としても何か変な化け方である。いつか、この対処方法と理由を考えてみたい。それにしても、週末の遊び道具としてはMathematicaは素晴らしいと思う。
1999-09-01[n年前へ]
■画像に関する場の理論 
ポイントは画像形成の物理性だ!?
今回は、
夏目漱石は温泉がお好き? - 文章構造を可視化するソフトをつくる- (1999.07.14)
の回と同じく、「可視化情報シンポジウム'99」から話は始まる。まずは、「可視化情報シンポジウム'99」の中の
ウェーブレット変換法と微積分方程式によるカラー画像の圧縮および再現性について
という予稿の冒頭部分を抜き出してみる。「コンピュータグラフィックスを構成する画素データをスカラーポテンシャルあるいはベクトルポテンシャルの1成分とみなし、ベクトルの概念を導入することで古典物理学の集大成である場の理論が適用可能であることを提案している」というフレーズがある。
着目点は面白いし、この文章自体もファンタジーで私のツボに近い。しかしながら、肝心の内容が私の趣向とは少し違った。何しろ「以上により本研究では、古典物理学の場の理論で用いられるラプラシアン演算を用いることで、画像のエッジ抽出が行えることがわかった。」というようなフレーズが出てくるのである。うーん。
私と同様の印象を受けた人も他にいたようで(当然いると思うが)、「エッジ強調・抽出のために画像のラプラシアンをとるのはごく普通に行われていることだと思うのですが、何か新しい事項などあるのでしょうか?」という質問をしていた人もいた。
また、話の後半では、画像圧縮のために、ラプラシアンをかけたデータに積分方程式や有限要素法などを用いて解くことにより、画像圧縮復元をしようと試みていたが、これも精度、圧縮率、計算コストを考えるといま一つであると思う(私としては)。
画像とポテンシャルを結びつけて考えることは多い。例えば、「できるかな?」の中からでも抜き出してみると、
- 分数階微分に基づく画像特性を考えてみたい- 同じ年齢でも大違い - (1999.02.28)
- ゼロックス写真とセンチメンタルな写真 - コピー機による画像表現について考える- (99.06.06)
- コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
現実問題として、実世界において画像形成をを行うには物理学的な現象を介して行う以外にはありえない。「いや、そんなことはない。心理学的に、誰かがオレの脳みそに画像を飛ばしてくる。」というブラックなことを仰る方もいるだろうが、それはちょっと別にしておきたい。
「できるかな?」に登場している画像を形成装置には、
コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
で扱ったコピー機などの電子写真装置や、
宇宙人はどこにいる? - 画像復元を勉強してみたいその1-(1999.01.10)
で扱ったカメラ。望遠鏡などの光学系や、
ヒトは電磁波の振動方向を見ることができるか?- はい。ハイディンガーのブラシをご覧下さい - (1999.02.26)
で扱った液晶ディスプレイなどがある。そのいずれもが、純物理学的な現象を用いた画像形成の装置である。
例えば、プラズマディスプレイなどはプラズマアドレス部分に放電を生じさせて、電荷を液晶背面に付着させて、その電荷により発生する電界によって液晶の配向方向を変化させて、透過率を変化させることにより、画像を形成するのである。
 |
また、逆問題のようであるが電界・電荷分布測定などを目的として液晶のボッケルス効果を用いることも多い。液晶を用いて得られる画像から、電界分布や電荷分布を計測するわけである。これなども画像と場の理論が直に結びついている一例である。
参考に、SHARPのプラズマアドレスディスプレイを示しておく。
 |
また、電子写真装置などは感光体表面に電荷分布を形成し、その電位像をトナーという電荷粒子で可視化するのであるから、電磁場を用いて画像形成をしているわけである。だから、場の理論を持ちこむのは至極当然であり、有用性も非常に高いだろう。そういった視点で考察してみたのが、
である。 同様に、画像圧縮に関しても、画像形成の物理性に着目することで実現できる場合も多いと思うのであるが、それは次回にしておく。
2000-07-15[n年前へ]
■外の世界を眺めてみれば 
ビデオ入力を活用しよう
先日、トランジスタ技術の2000/07号を読み直していた。読み直していたのは「色センサー」の記事である。有限会社レンテックが視覚障害者用の製品として発売しているものである。PICをよく使う人だったら、この記事を読んでいなかったとしても、多分よく知っている話だと思う。何しろ昨年の「第三回PICmicroデザイン・コンテスト」で優勝した作品だからである。PICと音声ICの数多い制限と、測定上の制限の中で、「(使用用途を考えた上での)安定した色名決定」を行うルーチンがとても苦労していて、読んでいてとても面白い。
個人的には、この「第三回PICmicroデザイン・コンテスト」で入賞している「マルチ・チャンネル分光器」と
みたいなものを組み合わせて、「5000円でできるパーソナル・マルチ・チャンネル分光器」なんてものを作ってみたいと思っているのだけれど、こちらはなかなか作業が進んでいない。それはさておき、この「色センサー」のように、持ち歩いて色々なところですぐに調べることのできる測定器というのはとても便利なものだ。そして何より、それを作っている側からしても面白いものである。そこで、私も試しに作ってみることにした。といっても、計測器を作り出すと仕事と区別がつかなくなってしまうので、ハード的に作業をするのは気分が全然のらない。そこで、PCに接続されているビデオカメラを用いて、ソフト的に作ってみることにした。やってみたことは、以前作成した「色覚モドキソフト」を、ビデオカメラからのリアルタイム入力用に作ってみただけである。
以前
ではインターネット上にある画像ファイルに対して、画像処理をかける「色覚モドキソフト」を作ってみた。コンピュータにネットワーク上のものが見える「色覚」を持たせて、ネットワーク上の画像について考えてみたわけだ。そして、ではそれを自分のPCの中にある画像ファイルをいじるようにしてみた。つまり、コンピュータに自分の中のものが見える「色覚」を持たせて、自分の中を覗いてみたのである。そして、今回はPCに接続されているビデオカメラを用いて、コンピュータに現実社会を眺める「色覚」を持たせてみることにしたのである。そんな現実社会を眺めることができて個性を持つコンピュータを通して、現実社会を眺めてみたいと思うわけだ。
最近の持ち歩き用の小型ノートPCにはビデオカメラが取り付けられているものが多い。例えば、こんな感じだ。
 |  |
 |  |
私もCasioのPalm-sizePCは使っているし、ノートPCにもUSB接続のビデオキャプチャーを取り付けている。こういう持ち歩けるPCに取り付けてあるビデオカメラを活用しないのは勿体ない、というわけで、以前作った
を改造し、で作ったtruecolorを合体させて、ちょこちょこっと作ってみたのがこれだ。- truecolor5.exe ( truecolor5.lzh 746kB)
例えば、次の画面はTVで放映している「ターミネーター」を見ているところである。一番左の画面がコンピュータのビデオカメラに写っているそのままの画面だ。そして、真ん中がリアルタイムに色調変換をかけている画面である。つまりは、「色覚に個性を持つ」コンピュータが眺めている「ターミネーター」である。また、一番右はシャッターを押したときに取り込まれた静止画像である。
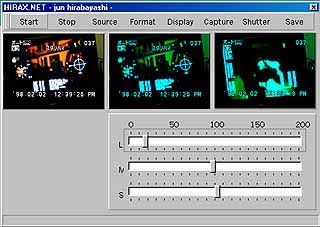 |
くれぐれも勘違いしないで欲しいのだが、上の一番左の画面で「赤い」部分が、真ん中の色調変換をかけた後では緑っぽく見えているからといって、このコンピュータがそこを「緑」と認識しているわけではない。あなたが、この真ん中の画面を見て何かを解釈しようとした瞬間に、それはコンピュータの感覚に加えてあなたの感覚が混入してしまうのである。もし、それでもそう考えたくなる人がいれば、そもそも「赤」とか「緑」という言葉はどういう意味なのかを考えてみると良い、と思う。
また、今回のL,M,S(これは具体的な何かを指すわけではないので、この意味についてはあえてここでは説明しない)の各スライダーの感度パーセンテージを以前のような0〜100%ではなくて、0〜200%の範囲で動かせるようにしてみた。もし、あなたのPCのモニタがこのLに対応するところが弱くなりがちならば、このLのスライダーをいじってやって、Lに関する情報を増幅してやることができる、と考える人もいるだろう。といっても、いじってみるとわかると思うが、そもそもモニタの出力可能な限界と画像フォーマット上の限界があるわけで、なかなかそういうわけにはいかない。ただ、色々と実験してみるのには面白いかもしれない。
ちなみに、次の画面は「週間アスキー」の広告を眺めている画面だ。おやおや、この広告はこのコンピュータには今ひとつアピールしないようだ。
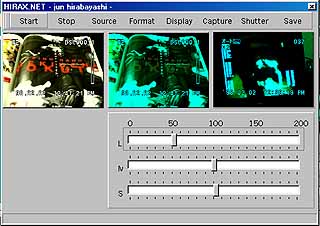 |
さて、先ほど
そもそも「赤」とか「緑」という言葉はどういう意味なのかを考えてみると良い、と思う。とあっさり書いたが、「言葉」とか、「現実」とか、あるいは「感覚」といったものはすこしづつ重なり合ってはいるけれど、それは一致し得ないものだと私は思っている。まして、それらは一人の人の中で完結できるものでもないし、同時に万人にとって同じでもない。以前書いた「クジラは哺乳類か魚か?」とかと同じで、心底考えてみることに意味があるんじゃないか、と思ってたりするのだ。