1999-09-20[n年前へ]
■深夜特急 '99 
HIRAX発ロンドン行きWEBの旅
新しい情報を探しに
お笑いパソコン日誌 (http://www2s.biglobe.ne.jp/~chic/pilot.html )を見に行くと面白い情報があった。それは、
Webの分離度合いは19クリック分?である。
( http://www.zdnet.co.jp/news/9909/10/www.html)
内容のポイントは
- 「Nature誌の9月9日発行号の掲載された2つの研究が明らかにしているように,WorldWide Webは急速に,1つの有機生命体としての進化を遂げつつある。Webの成長のダイナミクスとトポロジは,物理学の世界のPowerLawとして知られている法則に従っている」
- 「ネットワーク内の2点間の平均最短経路,つまり“直径”を求めることができる。Web上に8億のドキュメントがあるという推定が正しいとすれば,無作為に抽出した2点間の平均“距離”は19リンクになる。」
そうであるならば、ぐずぐずしてはいられない。もちろん、WWW.HIRAX.NETをスタート地点として、WEBの旅を続け、ロンドン中央郵便局を目指すのだ。平均“距離”が19リンクなら案外と近いかもしれない。WEB上で19回位のヒッチハイクをすれば良いことだ。そして、旅の最終地点であるロンドン中央郵便局からメールを出すのだ。「ワレトウチャクセリ」、と。(何のことか判らない人は沢木耕太郎の「深夜特急」を読むべし。)
そう決めた私はビールを片手にユーラシア大陸横断の旅に出かけた。さぁ、右手の親指を突き出し、ヒッチハイクのポーズで(Libretto50だから)、WEBの旅のスタートだ。
0 http://www.hirax.net/もちろん、旅のスタート地点であるwww.hirax.netだ。ここのTopページからの数少ないリンクサイトからLaboFinderへ飛ぶ。1 LaboFinder http://www.labofinder.org/まずは、Linkページへ飛ぶ。2 http://www.labofinder.org/links/links_index.html会員のWEBへのLinkページへ行く。3 http://www.labofinder.org/links/links_member_index.htmlここから、でわとしかずさんの「ある化学者の屋根裏部屋」へ行こう。4 http://www.asahi-net.or.jp/~av4t-dw/index.html次は、化学系サイトへのリンクへ。5 http://www.asahi-net.or.jp/~av4t-dw/link2chem.htmlそして、University of Leeds (United Kingdom)だ。6 http://chem.leeds.ac.uk/default.htmlここのTravel Informationを選ぶ。7 http://www.chem.leeds.ac.uk/Travel.htmlBritish Airwaysへ行く。8 http://www.british-airways.com/もちろん、Traveller's Guide to Londonだ。9 http://www.british-airways.com/london/Resourcesを選んで、10 http://www.british-airways.com/london/resource/resource.shtmlLondon on the Webへ行く。11 http://www.british-airways.com/london/resource/links/links.shtmlThe London Tourist Boardへ行って、12 http://www.londontown.com/Mapsを選ぶ。13 http://www.londontown.com/maps/St.James Parkへ行って、14 http://www.londontown.com/maps/index3.phtml?grid=H7右へ一回移動して、15 http://www.londontown.com/maps/index3.phtml?grid=J7&letter=&street=&titlegif=こんどは上へ移動する。16 http://www.londontown.com/maps/index3.phtml?grid=J6&letter=&street=&titlegif=
さぁ、Trafalger Squareに到着だ。この横にロンドン中央郵便局はあるはずだ。
やっと、Trafalger Squareの近くのロンドン中央郵便局に辿りついた。えっ、単なる画像じゃないかって?まぁいいじゃないの。ここまで、結構時間がかかっているんだから...何しろユーラシア大陸を横断したんだから。それに真っ直ぐ辿りついたわけじゃないし...
それに16回のクリックで辿りついたのだから、最初の19回という予想にも結構近い。
 |
トラファルガー広場をしばらく眺めた後、NotePCを抱えた私は郵便局員に聞いた(心の中で)。
「電子メールを出したいのですが?」すると、彼女(私の想像の中の郵便局員はもちろん女性だったのだ)は
「電子メールを出すのは郵便局からではありません。」と言った(心の中で)。
言われてみれば(心の中で)、電子メールは郵便局で出すのではなかったのだ。別にどこからでも出せるのだった。別にイギリスまで来る必要もなかったのだ。それならば、例えどこであっても私が決めればそこが旅の終点と決めた「ロンドン中央郵便局」だ。旅の終点の「ロンドン中央郵便局」の場所は私が決めれば良いことだったのだ。
何しろ、プロデューサーにゴールを決められているわけじゃないしね。
1999-12-04[n年前へ]
■WEBの世界の「力の法則」 
「ReadMe!JAPAN」と「日記猿人」に見るWEBアクセス数分布
以前、
の中で書いたように、「Webの成長のダイナミクスとトポロジは,物理学の世界のPower(累乗)Lawとして知られている法則に従っている」という面白い話が世の中にはある。これは、「ごく少数のWEBサイトへのアクセス、あるいはリンクが他を圧倒する程の割合を示す。」ということである。「インターネットのほとんどのアクセスというものは、ごく少数の特定のサイトへのものである。」ということだ。宇多田ヒカルの売り上げが演歌の総売上をはるかに超えるという話とよく似ている。実社会でもそういうことは実に多い。どうも、マイナー趣味である私には、Power(累乗) Lawというのはいま一つ面白くない話ではあるが、
- InternetEcologies
- http://www.parc.xerox.com/spl/groups/dynamics/www/internetecologies.html
- Paperson small-world networks
- http://www.ncrg.aston.ac.uk/~vicenter/smallworld.html
まずは、考えるためのデータを採取してることにした。欲しいデータは色々なWEBサイトへのアクセス数である。もちろん、自分のWEBサイトへのアクセスではないのだから、何らかの公開データを探さなければならない。
そこで、ReadMe!Japan(http://readmej.com/)と日記猿人(http://wafu.netgate.net/ne/)という二つのランキングシステムを用いてみた。ReadMe!Japanは日本語の「読み物」を主体としたWEBランキングである。また、日記猿人は名前の通り「日記」をターゲットとしたWEBランキングである。
一見、同じように見えるReadMe!Japanと日記猿人のランキングであるが、かなり違ったシステムである。以下に、Readme!Japanと日記猿人のランキングシステムを示してみる。
- Readme!Japan 登録したWEBページに、一日の間にアクセスしたIPアドレスの数。
- 日記猿人 「投票」ボタンを押した人(ブラウザー)の数、一日の間に一人の人(ブラウザー)が同一の日記に対して複数回の投票は行うことが出来ない。
一方、Readme!JapanはIPアドレスベースであるから、同一のProxyなどを経由したアクセスの場合、何人からアクセスがあろうと1pointである。しかし、読者に「投票ボタンを押す」というような作業は要求されない。
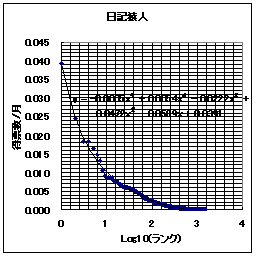
それでは、日記猿人とReadMe!JAPANの得票ランキングの例を示してみる。横軸はランク(順位)であり、縦軸が得票数である。ここでは縦軸・横軸共に線形軸を用いている。
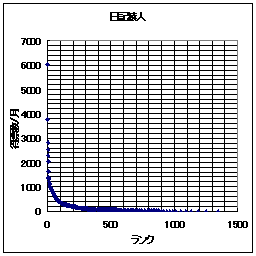 | 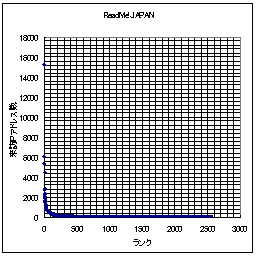 |
なお、 Readme!Japanは11/30日のものであり、日記猿人は(ほぼ)11月分の得票数分である。
このグラフを眺めてみると、日記猿人とReadMe!JAPAN共によく似ている。なるほど、少しランクが下がっただけで、急激に得票数が少なくなっている。もう、縦軸で言うならば下に張りついてしまっている。「ごく少数のWEBサイトへのアクセス、あるいはリンクが他を圧倒する程の割合を示す。」という「WEBの世界の力(累乗)の法則」は日記猿人とReadMe!JAPANでも当てはまるようである。
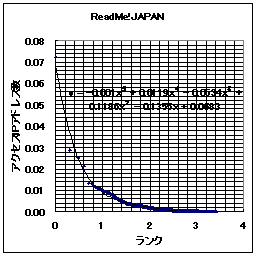
さて、ここまでランクに対して得票数が変化するとなると、グラフの軸は線形軸でなくて対数軸の方が良いだろう。そこで、グラフの軸を対数軸に変えたものを以下に示す。
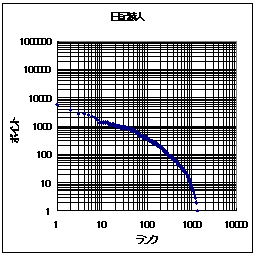 |  |
こうすると、日記猿人とReadMe!JAPANのどちらも、
- 上位のランク(例えば、1位から1000位程度まで)では傾きがほぼ1である。すなわち、ランクが一桁下がると、アクセス数も一桁下がる。
また、ReadMe!JAPANでは、ランクが極めて大きい所では得票数が0に近い。おそらく、その影響と考えられるが、ランクと得票数の関係が直線でなくなっている。
それと同じことは日記猿人でも言えるだろう、ただし、「ランクとポイントの関係が直線でなくなる」のがReadMe!JAPANよりも早いような気がする。しかし、それは誤差かもしれない。参加数もかなり異なっているので、誤差の可能性が高いと思われる。
さて、これまでは日記猿人とReadMe!JAPANのランキングの数字を直接用いてきたわけである。しかし、得票数の全く違うものをそのまま比較してもしょうがない。ある程度条件をそろえた上で比較をすべきであろう。そこで、縦軸を正規化して比較をしてみることにした。得票数の合計が1であるような単位に変換してみるのである。
ここで、横軸はランクのLog_10を用いている。本来、ランク(順位)も何らかの正規化の変換をすべきであろうが、今回はやり忘れた。きっと、頭が疲れているせいである。
また、グラフを見ればわかると思うが、それぞれについて近似曲線を計算している。
 |  |
次に、ここで得られた「ランクとポイントの関係」を示す近似関数
- ReadMe!JAPAN y = -0.001x^5 + 0.0119x^4 - 0.0534x^3 + 0.1186x^2 - 0.1355x+ 0.0683
- 日記猿人 y = -0.0005x^5 + 0.0054x^4 - 0.0222x^3 + 0.0472x^2 - 0.0589x+ 0.0391
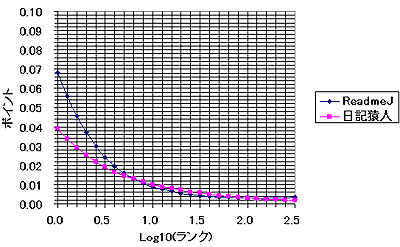 |
R eadMe!JAPANでも日記猿人でも横軸が2以上(すなわち100位以下)の場所などでは、ほとんどポイントはゼロみたいなものである。すなわち、100位より下のWEBのアクセス(本WEBへのアクセスも含めて)は誤差みたいなものなのだ。何しろ、一位(トップ)のポイントが0.07とか0.04とかなのだ。それは「一位のWEBサイトへのアクセスが全部のサイトへのアクセスの1割弱を占める」ということなのである。20位までのサイトへのアクセスを合計すると全アクセスの50%以上を占めてしまう。これが、恐るべきWEBの世界の"PowerLaw"、すなわち、「力(累乗)の法則」である。
ところで、日記猿人では上位サイト(すなわち、横軸で0に近いところ)での関係式の傾きがReadMe!JAPANよりも小さい。すなわち、上位サイトの得票数が拮抗している。これは一体何故だろうか?
私はこの理由を、
- 日記猿人の読者が割と似ている趣味を持っている
- 日記猿人の参加WEBサイトが似たような内容を持っている
日記猿人の参加WEBサイトが似ており、読者同士が割と似ている趣味を持っていれば(私も含めて)、得票数というのは当然横並びになるだろう。上位サイトにはほとんどの人が見に行き、そしてほとんどの人が「投票」ボタンを押せば、上位サイトはみな同じような得票数を示すことになる、と思うのである。
それは、違う傾向を示すReadMe!JAPANの中でも、読者層も作者も似ている「Fast&First」と「今日の必ずトクする一言」はとても近い得票数を示している、ということがその根拠の一つである。
それに対して、ReadMe!JAPANが比較的広いジャンルの「読み物」が集まっているのでそういう現象が見られないのだろう、と考えるのである。しかも、実際には「読み物」ですらないものも集まっているので、なおさらジャンルとしてはバラけている。だから、「WEBの世界の力(累乗)の法則」を素直に反映していると考えるのである。
私としては、ごく一部のWEBサイトへの集中が生じるのはツマラナイと感じてしまうのであり、「WEBの世界の力(累乗)の法則」はキライである。だからといって、趣味が似た人ばかりというのもツマラナイように思う。うーん、どういうのがツマラナクナイのだろうか?
それはきっと、「色々な趣味の人が色々なWEBへアクセスする」というのが私の好みだ。実現は難しいのだろうけど...いや、そんなことはないか。
1999-12-21[n年前へ]
■恋の力学 
恋の無限摂動
クリスマスが近くなると、街のイルミネーションが綺麗に輝き始める。いかにも、ラブストーリーが似合う季節である。そこで、今回は、"Powerof love"、すなわち、「恋の力」について考えてみたいと思う。「恋の力」により、人がどのような力を受け、人がどう束縛されるのか、などについて考えみたいのである。また、恋に落ちたカップルがどのような行動をするのかについて解析を行ってみたい。
「できるかな?」では以前、
において、カップルが他のカップルを意識する力について考えたことがある。カップル同士の間に働く斥力を考えることにより、鴨川カップルの行動を考えてみた。それと同様に、今回はひとつのカップルのみを考え、その中に働く力を考えてみるのである。ひとつのカップルの「男」と「女」の間にどのような力が働くかを考えるのである。そういうわけで、今回の登場人物は「男」と「女」である。その二人は「恋に落ちた二人」である。二人の間には「恋の力」が働いているのだ。その二人の間に働く「恋の力」について考察することにより、恋に落ちたカップルの行動について考察を行ってみることにする。
といっても、「恋の力」を精密に測定した報告例は未だ存在しないので、ここでは適当な値を用いていくことにする。「恋は距離に負けない」とか「遠くて近きは男女の仲」などとははよく言われる。そこで、距離によらないと近似した。また、「遠くて近きは男女の仲」の意味を考えれば、恋の力は無限遠まで働く力である、と考えるのが自然である。
そこで、今回の「恋の力」は距離に関わらず一定であると仮定した。距離=rとした時に-r/Abs[r]の大きさで「相手に惹かれる」ものとした。仮に第一種「恋の力」(仮称)とでもしておく。
今回は「恋の力」は距離によらないものとした。しかし実際は、(通所の距離においては)「男」と「女」は距離が近いほど惹かれ合うし、離れてしまうと惹かれ合う力は弱くなるというのが自然であると思われる。そこで今回の第一種「恋の力」(仮称)は、あくまで大雑把な近似ということにしておく。
恋する二人の間に働く力をもう少し正確に記述しておくと、
- 「恋の力」 = - 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「恋の力」=優柔不断度 * 「恋の加速度」
であることだ。心がトキメいてもなかなか行動を起こすことが出来ない人がいるだろう。そういう人は「優柔不断度」が高いというわけである。恋の行動における慣性を示すパラメータである。
また、今回は空間を1次元であると簡略化してみた。1次元の空間の中で「男」と「女」が動き回るのである。その時間的変化を調べてみるのだ。従って、シミュレーション結果は空間軸が一次元+時間軸一次元で、合わせて2次元となる。
さて、この「恋の運動方程式」を解くことにより、恋する二人の行動は予測することが可能となるわけだ。試しに、その計算サンプルを示してみる。なお、今回は時間方向で数値的に逐次解を求めている。
初期状態は
- 「男」位置=5, 速度=0,魅力=100,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
位置や時間の単位は任意単位である。「0」と「5」は東京と大阪であっても良いし、ロンドンとニューヨークであっても良い。あるいは、実空間でなく精神的な空間と考えてもらっても構わない。すなわち、心の動きを示しているものとするのである。
また、二人の「魅力」や「優柔不断度」は対等である場合だ。その結果を下に示す。このグラフは縦軸が空間位置であり、横軸が時間である。黒線が「男」であり、赤線が「女」である。
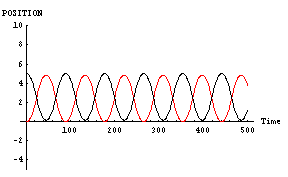 |
「男」と「女」が同じように相手の方向へ向かっているのがわかると思う。これが「恋の無限摂動」である。こういった「恋の無限摂動」の代表的なものには「君の名は」の主人公達の動きなどがある。恋に落ちた二人が、延々とすれ違いを続ける物語である。これは、この「男」と「女」の行動そのものである。
この計算結果では「男」と「女」が糸を紡いでいるようにうまく絡みあっているのがわかる。「恋の無限摂動」の幸せなパターン例である。これは、「男」と「女」が対等であったことがその一因である。
その証拠に、「男」と「女」が対等でない場合の計算結果を示してみる。次に示すのは、
- 「男」位置=5, 速度=0,魅力=10,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
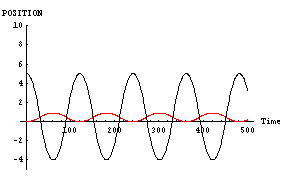 |
「男」が右往左往するのに対して、「女」はほとんど動いていないのがわかると思う。おそらく、この場合には「男」と「女」の「心」もこれと同様のパターンを示しているものと思われる。すなわち、「男」の「心」は揺れ動いているのに対し、「女」の「心」はほとんど動いていないのである。
先の例と異なり、これは実に不幸な計算例である。不幸ではあるが実際によくある例であると思う。以降、これを「男はつらいよ」パターンと呼ぶことにする。「女」に「男」が振り回されているパターンだ。もし、奇跡的に結婚などしても、将来どうなるかは火を見るより明らかである。
それでは、「男」と「女」の「魅力」が同等で、かつ、とてもスゴイ場合を示してみる。すなわち、ドラマの主人公達のようにとてつもなく魅力的な二人が恋に落ちた場合である。一般人とは違う二人が恋に落ちたら、果たしてどのような行動を示すのであろうか?この場合のパラメータは以下に示す、
- 「男」位置=5, 速度=0,魅力=1000,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=1000,優柔不断度=10
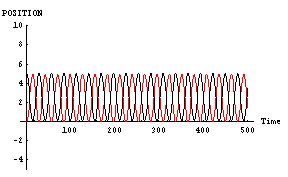 |
「魅力ある二人が恋に落ちた場合には、あまり近づかない方が良い」という教訓をここから得ることができる。
最後に、「男」と「女」の二人ともにあまり魅力がない場合である。パラメータとしては、
- 「男」位置=5, 速度=0,魅力=2,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=2,優柔不断度=10
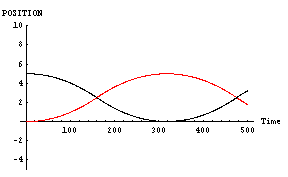 |
これなど「恋」と言えるのかどうかもわからない位である。ほとんど、「ただすれ違っただけの相手」である。これがさらに進むと、魅力がお互いに0同士のパターン、
- 「男」位置=5, 速度=0,魅力=0,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=0,優柔不断度=10
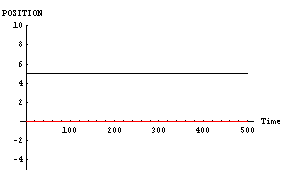 |
これっぽっちも「男」と「女」は「恋」に落ちていないのである。これではカップルの「男」と「女」ではなく、単なる他人である。
さて、今回は行わなかったが、カップルに「恋のエネルギー損失」を導入することにより、「恋の無限摂動」を減衰させることができる。それにより、現実のカップルの行動にさらに近づくことができるのではないかと、私は考える。何らかの抵抗が生じることにより、「恋の無限摂動」が減衰するのだ。そして、二人は接近した状態で停止するわけだ。
さて、今回の登場人物は「男」と「女」だけであった。しかし、現実でも、ドラマの中でも、通常は多くの登場人物が登場する。登場人物が「男」と「女」だけというような理想的な条件のみではない。
人の恋路を邪魔する(主人公からすれば)ヤツも必ず登場する。また、特定の登場人物の間では斥力が働くだろう。そのような場合、一体どのような現象が生じるのだろうか。
そもそも、今回の恋する二人の行動パターンは予測可能であったが、現実そのようなことがあるだろうか?果たして、未来の行動パターンは予測可能なのだろうか?色々な登場人物が現れる場合にも、今回の結論は成立するのだろうか?
それらは次回の課題にしておく。題して、「恋の力学 三角関係編- 恋の三体問題- (仮称)」である。「恋の力」を一般化し、多体問題として解いてみたいのである。恋する人達とその周りの人達がどのような行動をするか、恋の三角関係においてどのような力が働いているのか、について解析を行ってみたい。今回は、そのための前準備というわけである。
2000-01-13[n年前へ]
■WEBサイトの絆 
WEBの世界を可視化しよう
目に見えないものを実感できるものにしようと思うことは多い。「直接感じることが出来ないものを感じられる形にする」という作業とその結果には非常にわくわくさせられる。それは、きっと私だけではないと思う。
目に見えないものは色々ある。可視化して見てみたいものは多々あるのだが、以前、
の時に扱った、WEBのトポロジーなどもその最たるものである。WEBページはもちろん目に見えるわけではあるが、それらがどう繋がっているか、すなわち、WEB[= クモの巣(状の物);織物 ]そのものは目には見えない。ネットワークという目に見えない世界でWEBサイト同士がどう繋がっているか、それは企業のWEBサイト同士であれば企業間の繋がりを示すかもしれないし、公的機関のWEBであれば公的機関内部の繋がりが見えてくるかもしれない。そして、個人WEBであれば、個人どうしの繋がりが見えてくるだろう。そして、さらに考えを進めるならば、それが「WEBの繋がりだ」と端的に言い切ってしまっても良いと思う。
そういう色々なWEBサイト同士が互いに結びつき合う、つまりWEBそのものを今回は可視化してみたい。その結果はきっと「WEBサイトの絆」を私に見せてくれるはずだ。
例えば、ファイルシステムを可視化するものであれば、
- xcruise( http://tanaka-www.cs.titech.ac.jp/~euske/index-j.html )
そして、今回の本題のWEBサイトのHyperlink構造を可視化するソフトウェアも、少し探しただけでも結構ある。例えば、
- Site Manager
- ( http://www.sgi.com/software/sitemgr.html )
- HyperLINKWWW Visualization/Navigation
- ( http://www.acl.lanl.gov/%7Ekeahey/c3/navigate/navigate.html )
しかし、よく調べていないので間違っているかもしれないが、この辺りのソフト(appleを除く)はWEBサイト内のリンクのみに限られるようである。それでは、今回の目的とは違う。何しろ、今回知りたいのはWEBサイト同士のリンクの度合いである。WEBのトポロジーなのである。
そこで、もう少し探してみる。すると、今回の目的にかなり近い情報が
- Web構造の把握 宮久地博臣 都立科学技術大学大学院 平成9年度修士論文
- ( http://home2.highway.ne.jp/miyakuji/shuron.html )
やり方はどうしたら良いだろうか?宮久地氏と同じようにWeb Robotを作成して、データを集めるのが理想的だろう。しかし、「perl入門」を昨日やっと買ったばかりの私にはとても難しそうである。いや、もしそんなことをしたらとんでもないことになるに違いない。
そこで、perlのlwp-rgetを用いて各WEBの内容をローカルのPC内にダウンロードした上で、勉強がてらperlで解析を行うことにした。と、思ったのだが、lwp-rgetが上手く動いてくれない。まだドキュメントをちゃんと読んでいないせいだろうか?何故か、ダウンロードの途中で終了してしまう。仕方がないので、急遽作戦を変更し、ダウンロード作業はlwp-rgetではなくてwgetを用いることにした。
行った手順は以下のようになる。
- 5つのWEBサイトを広いWEB内から適当に選択する
- 選んだ各WEBサイト内のファイルについて、相互のハイパーリンクを抽出し、その数を解析する
- その結果を可視化する
以下に、解析を行った結果、すなわちサイトA,B,C,D,Eの相互に対するリンク数を示す。
| ↓から→へのリンク数 | |||||
0 | 2 | 0 | 27 | ||
1 | 0 | 13 | 273 | ||
20 | 2 | 0 | 43 | ||
0 | 11 | 0 | 285 | ||
1 | 1 | 1 | 1 | ||
合計 | 22 | 14 | 3 | 14 | / |
サイトE「日記猿人」へのリンクがムチャクチャ多いのは投票ボタンという形で、他のサイトからリンクがなされているからである。
さて、上の表からではWEBの絆を実感できないので、「WEBの絆」を3次元空間に可視化するJavaアプレットを以下に張り付けておく。WEBサイトが5つあるので、それぞれのサイトをピラミッド構造(四角柱状)に配置した。
各WEBサイトの表示色は、
- A = 赤
- B = 緑
- C = 青
- D = 黄
- E = 灰
それぞれのサイトから伸びる直線の長さは、そのサイトから他のサイトへ向かうリンク数に比例したものにしている。また、直線の太さもリンク数に比例させている。また、それぞれのWEBサイトを示す立方体の大きさは自分へ向かうリンク数に比例させている。ただし、サイトEの大きさはあまりにも巨大なため、リンク数に比例したものにはなっていない。また、サイトE、すなわち「日記猿人」、へのリンクは省略し、全てサイトEからの直線リンクを表示するだけにした。
さぁ、WEBサイトの構造を自分の目でみて、そしてグリグリ動かして見てもらいたい。このグラフの操作方法は
- 操作 = 作用
- マウス左ボタンドラッグ = 回転
- シフトキー + 垂直ドラッグ = ズームイン・アウト
- シフトキー + 水平ドラッグ = 垂直軸についての回転
- コントロールキー + 垂直ドラッグ = 焦点距離の変更
- マウス右ボタン垂直ドラッグ = 部品除去
- "s"キー = ステレオ画像作成
Java表示が上手く動かない人のために、静止画も一応張り込んでおく。
 |
どうだろう?この5つのWEB間のWEB構造から何が見えるだろうか?こういう解析を数多くのサイトに行うと非常に面白い結果が得られそうである。特に「日記猿人」のようなコミュニティーに対して行うと興味深い結果が得られるはずだ。
私のような「日記猿人」の日記はほとんど読まない(サイトAに関しては大ファンであるが)人間にとっても興味深いのであるから、関係者にとってはきっと...の筈だ。
さて、今回はテストのためにごく少数(5つ)のWEBの解析を行ってみた。いつか、こういった解析を広い範囲で行い、そして、時系列的な変化をも調べようと思う。銀河のvoid構造が観測され、可視化されたものを見たときもとてもわくわくしたものだが、WEBの構造・変化ならばどうだろうか?
不思議なことに、そういうことを考えていると、「新宿都庁」と「思い出横町」が頭の中に浮かんできてしまうのは何故だろうか?押井守の影響だろうか。謎である。
そして、こうも思う。WEBネットワークの中でWEBサイトは何を感じているのだろうか?これらのWEBサイトはもしかしたら孤独を感じているのだろうか、それとも繋がりを感じているのだろうか?あの時のページの中の一フレーズがその答えの一つなのかもしれない。
2001-01-04[n年前へ]
■世界の国からこんにちは 
hirax.net版GeoWhoisを作る
VisualC++ MFCを使ったWindowsプログラミングはどうもお気楽という感じにはいかない。もちろん、「子供の科学」にすらMFCを使ったプログラミング入門が連載(何故、VisualC++で!?)されるくらいであるから、別にそれが難しいわけではないのかもしれない。しかし、VisualC++MFCでWindowsプログラミングがキライになる人は絶対いるはずだ。現に突撃実験室のwebmasterはかつてVisualC++と闘った結果、「俺は永遠に組み込み屋じゃっ」と叫んでいたらしい(C.突撃実験室)。
私も含めて、そんなWindowsプログラミング難民達を優しく女神のように迎えてくれるのがBorlandC++Builderである。いや、女神は必ずしも私たちを優しく迎えてくれるわけではない。むしろ、女神は私達を冷たくあしらうことの方が多いので、実は女神よりもC++Builderの方が優しいと言っても良いくらいである。しかも、C++Builderは自然にWindowsプログラミング(そして嫌でもDdelphi)を覚えさせてくれるところが実にありがたい。そして、そんなC++Builder(Delphi)ユーザー達にとって実に便利なのがTorry'sDelphi Pages.だ。
というわけで、先日Torry's Delphi Pages.をチェックしていると、とても面白いコンポーネントがあった。それはYehudaSharvit.による
である。ドメインネームから地理的な位置座票への変換を、地理データベースを持っているイリノイ大学の"cello.cs.uiuc.edu"を使って行い、そしてゼロックスのパロアルト研究所(parc)の"mapweb.parc.xerox.com"から地図画像をダウンロードして表示するコンポーネントである。ドメインネーム->持ち主の住所(WHOIS)→位置座票("cello.cs.uiuc.edu")->地図表示("mapweb.parc.xerox.com")という流れでドメインが位置している場所を表示するわけだ。 例えば、DelphiでGeographicWhois Componentを使ってapple.comを検索・表示してみたのが次の画像である。
 |
もちろん、「ドメインが位置している場所」と言っても、ドメインの登録者の住所を表示するわけで、必ずしもそのドメインのサーバーが位置する場所を表示するわけではない。だけど、そもそも「ドメインが位置する場所」というのは「実際のドメインのサーバーが位置する場所」ではなくて、「ドメインの登録者の住所」だと私は思うのでこれはこれで良いのである。そしてまた、「ネットワーク上であまり意識することのない地理的な位置情報を表示する」というのがかなり面白いと私は思う。
日頃、ちょこちょことブラブラと色々なサイトを巡回して楽しんでいる(といっても実は多くはない)のだが、そのサイト達は世界中のどこにいるのだろう?なんて時折と思うことがある。以前、
でネットワーク上を自分の家からロンドンまでヒッチハイクしてみたけど、そんなヒッチハイクも地理的な位置情報が判れば、それはもっと楽しいかもしれない。WEBで辿る「世界一周の旅」なんてのも簡単にできることだろう。そしてまた、「インターネット上の距離」と「地理的な距離」を並べて見てみるのも面白いだろう。というわけで、今回は色々なサイトがどんな場所に位置しているかを表示するアプリケーションを作ってみることにした。ところで、先のGeographicWhois Component自体はDelphi用のコンポーネントでC++Builder用ではない。もちろん、C++BuilderはPascalで書かれたDelphi用のコンポーネントだって読み込めるわけだが、とりあえずこのコンポーネントはそのままではC++Builderには取り込めない。それだけではなく、地図の縮尺や位置などの指定をすることができないため、このままでは色々なサイトの位置を重ねて表示することはできない。
そこで、「ドメインネーム->持ち主の住所(WHOIS)→位置座票("cello.cs.uiuc.edu")->地図表示("mapweb.parc.xerox.com")というルーチン」をC++Builderで自分用に作り、できあがったアプリケーションがこれである。
もちろん、いつものように数回だけの動作(不?)確認しかしてない完全無保証版である。 GeoWhois.exeの動作画面が次の図である。ドメインの場所を検索しその結果が上の方の画像に表示される。また、検索履歴が下の画像に表示される。検索履歴画像の方はSaveボタンでbmpファイルとして保存することができる。
検索履歴が下の画像に表示される。  |
ちなみに、上の画像の検索履歴は私のよく見に行くところである。結構世界の各地に広がっているような気もするし、広がっていないような気もする。こんなプロットをもっともっと重ねてみて、あとリンクの様子も線でプロットしてみたりすればかなり面白いグラフができることだろう。
さて、ドメイン名から位置座票への変換("cello.cs.uiuc.edu")はあまり色々な場所が登録されているわけではないので、少なくとも日本などでは東京くらいしか変換することができない。だから、当然のごとくtomoya.comやhirax.netは表示されない。だから、実際のところ私が良く見に行く個人サイトは本当はあまり検索することができない。もちろん、プロバイダー内にWEBページを持っているようなところは検索・表示することができるのだけれど、そんなところはみんな東京になってしまうのである。しかも「WEBページの持ち主= ドメインの持ち主」でもないので、そもそも「そのドメインの位置情報 = WEBページの位置情報」では全然無い。だけど、そもそもそんな日本国内の「ご近所さんを探せ!」コーナーではないのだから、もうそれはそれで良いのである。遙か遠くの国のサーバーを地図で眺めることができる、というところが良いのである。
このGeoWhoisを応用していけば色んな遊び方があると思うのだが、今回はこのアプリケーションを作ってみたところで終わりにしたいと思う。次回以降(といってもいつになるか判らないけど)で、「インターネット上の距離」と「地理的な距離」でも調べてみたいと思う。
それにしても、こんな地図を眺めていると、本当に旅行したい気分になってきたぞ〜