1999-02-14[n年前へ]
■感温液晶でNotePCの発熱分布を可視化する 
熱いところで感じてみたい St.Valentine 記念
東急ハンズで実験材料をいくつか買った。その中から、感温液晶シートを使って計測を行ってみたい。
色が変わる材料というものは多い。温度により物質の色がかわる現象はサーモクロミズムと呼ばれる。光により色が変わるサングラスのような現象の場合はフォトクロミズム呼ばれる。けっこう、色々な応用を見かける。
通常の感温液晶はコレステリック(Cholesteric)効果により反射光のスペクトルが変わるため、色が変化する。
これが感温液晶シートである。よくで見かけると思う。
 |  |
さて、それでは感温液晶を使っていくつか測定を行ってみたい。まずは、NotePCの発熱分布を調べてみる。最近のNotePCはかなり熱くなるものが多い。暖かいというよりもアッチッチ状態になるものさえある。
それでは、
- Toshiba Libretto50
- Panasonic Let'sNote mini(AL-N4)
いずれも、感温液晶シートをNotePCの上に載せることにより、評価を行っている。今回は発熱分布を知ることが目的であるので定量的な評価は行っていない。もし、温度を定量的に行いたいのであれば、色と温度の対応曲線をあらかじめ測定する必要がある。
以下に結果を示す。
 |  |
 | 左上:上面 右上:上面の発熱分布 左下:下面の発熱分布 |
 |  |
 | 左上:上面 右上:上面の発熱分布 左下:下面の発熱分布 感温液晶シートのサイズがA4であるため、Let'sNote miniにちょうどフィットする。 |
Libretto50ではPCカードのNICを右に挿しているため、キーボードの右側部分の発熱が大きい。また、下面ではハードディスク部分の発熱がわかる。また、ク*ックア*プしているせいかかなりアッチッチである。
Libretto50,Let's Note miniいずれにおいても液晶のドライバーがある部分(液晶の左)は発熱が激しいのがわかる。
本来ならば、愛用しているTOSHIBA Portege320でも計測を行いたい所だが、ただいま長期入院中である。間もなく使用1年になるが、これまでに入院3回を経験し、入院期間は計2ヶ月にわたる。昔の小説家もビックリの病弱さである。他の使用者の話を聞いていても実に不安定な機種のようだ。一体、疲労骨折を経験していないPortege320というのは、はたして存在するのだろうか。あぁ...
今回は手元にあったNotePCでのみ測定を行ったが、近所の協力の下に色々なNotePCの発熱分布を調べる予定である。特にパームレスト周りの発熱分布などは割に軽んじられているだけに、興味がある。
今回は感温液晶を使った温度分布の簡単な可視化をしてみた。同じような測定は色々してみる予定である。
感温液晶と同じように、温度で変化する材料は多い。例えば、FAXでよく使用される感熱紙もそうである。
他にも、RICOHの熱可逆性情報表示フィルム
http://ext.ricoh.co.jp/saiyo/sin/prof/eyes/page4_2.html
などもそうである。
これなどはお店のポイントカードなどでよく見掛ける。私の財布から探してみると、オートバックスのポイントカードがこれと同じようなものである。70-130℃位の温度変化により透明度を変化させる材料である。これ位の温度であると、真夏の車中にカードを放置するとどうなるか心配なところである。
今回の情報に関連するWEB一覧
- 伊藤のホームページ(http://www.infonia.ne.jp/~itous/)
- 岡山県教育センター(http://www.pref.okayama.jp/kyoiku/sido/edu_cent/seminar/rika/rikasho/zikken.htm)
- お湯で変色するサーモクロミズム化合物をつくる(高橋 正)(http://www2b.biglobe.ne.jp/~murasho/news22.htm)
- 液晶について(http://www.osakac.ac.jp/labs/fujita/asai/ekisyo.html)
- 感温液晶を用いた非定常熱伝達の計測システムの基礎的研究(http://village.infoweb.ne.jp/~fwhz0564/kenkyu.htm)
- 感温液晶マイクロカプセルによる可視化(http://koneeko.linux.or.jp/AandO/gfd_exp/exp_j/tech/elc.htm)
1999-12-30[n年前へ]
■6502と並列計算とムーアの法則 
人間のクロック&スケールアップ
「物理の散歩道」を読み直していると、とある文章に興味を覚えた。
- 第五物理の散歩道 ロゲルギスト著 岩波新書
「通信を考える」の中の興味を惹かれた部分は「信号の伝わる速度と距離と処理速度の関係」を論じている部分だ。例えば、計算機は処理速度を高めるためには回路の大きさを小さくしなければならないとか、人間の頭脳の働きの速さから集団生活の広がりの限界について論じているのだ。例えば、
- 計算機の演算速度の時間スケール -> ナノ秒 = 10^-9s (クロックで考えると、1GHz)
- 人間の演算速度の時間スケール -> サブ秒 = 10^-1s (クロックで考えると、10Hz)
つまり、通信の速度が光速度であるとして、演算の単位クロックの間に通信が行われなければならないとするならば、計算機の時間・空間スケールと人間の時間・空間スケールは等しいだろう、という推論だ。
そして、さらにロゲルギストの想像は広がり、並列計算についても論じている。
計算機が東京と大阪に離れて置かれていて、通信をしながら作業をするとしたら、人間の場合にはそれと同じ条件というのはどんなものだろうか、と彼らは考える。それは、光の速度で55時間、ちょうど冥王星の軌道直径の5倍程度の空間スケールになる、と論じている。それ以上、離れた場合には演算の過程を共に行うのは無理ではないかというのである。
こういう文章を読んでいると、この文章が作られたのが30年以上前であることを忘れてしまいそうである。この人達の思索の自由さに憧れを感じてしまう。この人達は、頭の中にタイムマシンにでも持っているのだろうか、と感じてしまうのだ。
ところで、私がコンピューターをいじるようになった頃は、Apple][の時代だった。といっても、私はお金があふれていたわけではないので、XXX電子でAplle][のコンパチ基盤を買って組み立てて使っていた。その基盤上の6502は1MHzで動いていた筈だ(あぁ、I/Oの6809派vs6502派の論争が懐かしい!)。
それから20年程たち、CPUのクロックスピードは1GHzを越えようとしている。20年で1000倍である。そして、その集積度は、ムーア(GordonMoore)の法則の「半導体の性能と集積は、18ヶ月ごとに2倍になる」に従っている。
それでは、人間はどうだろうか?人間の脳味噌のクロックがどの程度であるか測定されているかどうか、素人の私にはよくわからない。しかし、WEB上のデータとしては、例えば
- Mayo's Profile( http://www.ceres.dti.ne.jp/~mayo/profile.html )
ロゲルギストの時代、すなわち30年以上前、から現在のMayo's Profileの値がほとんど変わっていないように、人間の演算スピードは変わるようなものではない。それは、そうだろう。ヒトのクロックスピードや集積度といったものは、変えるわけにはいかない。当然である。CPUと違ってプロセスルールを変化させるというような訳にはいかないのだ。
それでは、演算性能を上げようとしたらどうするだろうか?そうなると、並列計算を行うのが自然だろう。単独のCPUの性能を上げるわけに行かなくても、共同作業を行えば、演算性能を上げることができる。
現代はほとんどの作業が共同作業で行われる。また、その共同作業も大人数が関わるようになってきている。それは、どんな業種でも同じだ。一人では、なかなかできないことが多くなっている。
それら共同作業、すなわち並列計算、を行う人達(例えれば並列計算機における各ノード)を増やし、それらの間の情報転送をすばやく行うことが多くの作業(計算)を行うための手順だろう。
そこで、
で用いた- 人口増加( http://www.t3.rim.or.jp/~kabutoya/KABHTML/Yoi/2-1.html )
 |
なるほど、人間界の並列計算機におけるノード数は増加している。そして、各ノード間の通信速度を調べるために、まずは、
- 来て、見て、触って、情報伝達
- ( http://www.f-jhs.fukuoka-edu.ac.jp/3-3/jyoho.html )
西暦 内容これを全部転送速度に直してみる。といっても、よくわからない部分も多いので、私が適当に決めてみる。それでは、その変化を示してみよう。とりあえず、ここ200年位の間のものを考える。
-4000 のろし
-2400 伝書鳩
-2300 馬による伝令制度
1837 モールス電信機
1876 ベグラハム=ベル電話機
1909 グリエルモ=マルコーン無線電話機
1973 Ethernet XeroxPARCで生まれる。(ちなみにEther=エーテル)
1979 DIX規格=10Mbps
1992 FastEthernet=100Mbps
西暦 内容という感じだ。グラフにすると、
1837 モールス電信機 = 2bps
1909 グリエルモ=マルコーン無線電話機=10kbps
1979 DIX規格=10Mbps
1992 FastEthernet=100Mbps
 |
こんな感じである。対数グラフにおいて直線的に情報伝送速度が速くなっている。この関係は結構きれいである。
別に意図してこういう数字にした訳ではないのだが、不思議なことである。
このようにして、人間(ノード)間の転送レートが高くなることにより、先のような人口増加に伴うトラフィック増加をしのぐことができていると考えることもできるかもしれない。そして、人間達の共同作業、すなわち並列計算、を行うだけのバススピードを確保しているのである。
最近、会社組織などで分社化とか事業分割とかの話題をよく耳にする。こういった時に、分割における時間と空間のスケールはよく考える必要があるだろう。分割が有効なのは、ほとんど独立なものを分割する場合のみである。並列計算における領域分割などと同じだ。
共同作業がほとんどなく、結果のみをやりとりすれば良いような場合には分割による効果はあるだろう。その一方で、同じ事業・作業を行っているところが、離れていては作業の効率は上がらない。もし、技術系の会社でそのようなことを行うのであれば、事業や部署を並列化した際の真面目なシミュレーション位は行うべきだろう。いや、別に深い意図はないけど。
こういったことは「新・闘わないプログラマ No.109 時代錯誤」に書かれていることとも少し似ているような気がする。
さて、1999/12/30-2000/1/1は野沢温泉で温泉&スキーである。2000年問題で会社に泊まり込む人も多いが、私はスキー場で泊まり込みである。同時期に野沢温泉に行く人がいるならば、ぜひ一緒に「スキー場の特殊相対性理論」について討論したいと思う(スキー場で)。
2000-08-13[n年前へ]
■WEBの時間、サイトの寿命 
ゆっくり長く続けましょうか?
以前、
でロゲルギストが- 第五物理の散歩道 ロゲルギスト著 岩波新書 「通信を考える」
- その系の情報処理の単位時間
- その系の信号の伝わる速度
- その系の空間スケール
- 空間スケール < 情報処理の単位時間 × 信号の伝わる速度
- 大人数から構成される企業のスピードは、少人数から構成される企業のそれには遙かに及ばない
ところで、ロゲルギスト達はある系の「単位時間・信号伝達速度・大きさ」の間の関係について、
- 「単位時間・信号伝達速度」を入力値として、「大きさ」を考える
- 「大きさ・信号伝達速度」を入力値として、「単位時間」を考える
さて、寺田寅彦が「単位時間・信号伝達速度・大きさ」について、さらにどのようなことを展開していたかというと、それはある系の「大きさ・寿命」についての関係である。寺田寅彦は
- 空想日録 三 身長と寿命 (寺田寅彦随筆集 第四巻 岩波文庫 小宮豊隆編)
- 人体感覚について振動感覚の限界を調べた実験データ、 - 人は自らの体の固有振動周波数の振動に対してもっとも過敏である- 、というものをきっかけとして、
- 生物の時間の長さの単位は相対的なものである
- ある系の「時間の長さの感覚 = 相対的な単位」はその系の固有周期と密接な関係がある(振り子時計なんてわかりやすいだろう)
- ある系の「寿命」を測る単位は、その系の「時間の相対的な単位」、すなわち、その系の固有周期だと想像してみよう。
- その場合、ある系の固有周期はその系の大きさに比例するから、大きい動物ほどその系の「時間の相対的な単位」は長いものとなり、見かけ上の「寿命」はその動物の「大きさ」に比例するだろう。
なるほど、サイズが小さい動物(すなわち固有振動の波長の短い動物)にとっては、ほんの小さな変化も大きな変化である。ということは、その動物の感じる「時間単位」は短くなければ、生き残れないだろう。逆に、サイズの大きな動物は俊敏な動きはできないわけで、その動物の「時間単位」は長くならざるをえないだろう。
ゾウのような大きい動物は「時間単位」が長く、一見「寿命」が長いように見え、ノミのような小さな動物は「時間単位」が短く、一見「寿命」が短く見えるというわけだ。実は、ゾウもノミもその動物自身の「時間単位」を基準にすると、同じ寿命を生き抜いているということになる。
本川達雄の中公新書「ゾウの時間 ネズミの時間」では- 体重の4分の1乗に比例して「その動物の時間単位=生理的時間」が長くなる-と述べられているが、昭和八年に既に寺田寅彦は体重は身長の3乗に比例する、逆に言えば体重は身長の3分の1乗に比例するから、「体重の3分の1乗に比例して時間が長くなるだろう」と想像を巡らせているのである。素晴らしい、想像力である。
さて、寺田寅彦はロゲルギストと違って、「単位時間・大きさ」については言及しているが「信号伝達速度」については触れていない(その替わり、さらに「寿命」にまで触れているわけであるが)。もっとも、私があえて書き加えてみるならば、ある系の固有振動にはその系の中での弾性が密接に関係するし、弾性はその中での弾性波の速度も密接に関係する。つまり、ある系の固有振動の周期というものには「その系中での波の伝達速度」が暗に隠されていて、寺田寅彦は単にそれを一定とおいていたわけで、寺田寅彦が述べた内容は実はロゲルギスト達の述べた内容を包括している、と私は思うのである。
このような「単位時間・大きさ・信号伝達速度・寿命」に関する話は動物に限るものではない。
- ロゲルギストが「信号伝達速度=光速度」として、「処理速度を確保する」ための人類の行動範囲について論じたり、
- 私(いきなり自分を例に出すのも何だが)が「信号伝達速度の変化」と「大きさ(人口)の変化」から人類の処理速度の変化について論じたり
さて、前振りが長くなった。前回、
では、単に「信号伝達速度の変化」と「大きさ(人口)の変化」を並べて「処理速度」の変化について考えてみただけだった。今回は寺田寅彦が考えたのと同じく、「信号伝達速度」と「大きさ(人口)」から「寿命」が決まると考えることにより、「人類」の「寿命」の変化について考えてみることにしたいと思う まずは、前回使った「人類の大きさ=人口」の変化が次のグラフである。ただし、この人口は全然正確ではないし、むしろかなり不正確なものであることは先に断っておく。ここでは、細かな値を使うのが目的ではないので別に構わないだろう。
 |
そして、「人類」の中での「情報伝達速度」の変化を示したものが次のグラフである。この速度が「人類」という集合体の中での波の進行速度を決めるのである。
 |
それでは、「人類」という集合体の固有振動はどうやって扱うかというと、この
- 「人類の大きさ=人口」
- 「情報伝達速度」
- 人口 / 情報伝達の速度
その、人口 / 情報伝達の速度 = 「人類の固有時間」を計算してみたものを次に示してみよう。
 |
こうしてみると、人類というヒトの集合体においては、どんどん時間の流れは速くなり、それに応じて見かけの「寿命」は短くなっている、ということがわかる。人類はまさに生き急いでいるのである。もし、この流れを止めようと思ったら、どうしたら良いだろうか?それには、今回の計算から言えば情報転送速度を遅くするか、人類の大きさを大きくするしかない。情報転送速度を遅くするのはなんとも後ろ向き(byわきめも)だし、人口を減らすというのもなんとも後ろ向きだ。だとしたら、宇宙へでも人類が進出して、人類の空間的なスケールを大きくしていくしかないのだろうか?これもまた難しい話である。
さて、最近、大好きなWEBサイトが閉鎖してしまったり、更新速度が遅くなっていたりしていて少しさみしい。だけど、もしかしたら各WEBサイトにも、「更新速度が速いと、WEBサイトの寿命が短い」なんて法則が実はあるのかもしれない。更新速度が速いということは、そのWEBサイトの固有時間が速く流れているということで、限られた寿命をどんどん使い果たしているのかもしれない。
だとしたら、更新速度が遅いということはそのWEBサイトの寿命が長くなるということだから、それはそれで良いのかなぁ、などと思ってみたりする。「太くて短い寿命」も「細くて長い寿命」も実は本人からすればどちらも同じ長さなのかもしれないけれど、外から見ている私は「細くても良いから長く続いて欲しいなぁ」なんて思ってもみたりするのである。
2001-01-13[n年前へ]
■オッパイ星人の力学 第四回 
バスト曲線方程式 編
先日、父から封書が届いた。二十一世紀にもなったというのに、e-mailでもなくて封書が届いたのである。これは、やはりアレだろうか。いい年にもなってるのに、クダラナイWEBサイトを立てているデキの悪い息子を厳しく叱るためだろうか?しかも、そのクダラナイWEBサイト(しかも、有害公式認定サイト)の名前が自分の名前(hirax)だったりするからだろうか?それとも、「本が出たなら送れ」とは言われても実は送りたくなかった「あの本」を、少し前に父に送ってしまったからだろうか?いや、それとも…そんなこんなでドキドキしながら封筒を開けると、記事のコピーが二つ入っていた。他には何も入っていないのである。一体これは何の記事だろう?と思いながらそのコピーを眺めてみた。すると、まずひとつは去年の12月25日付けの毎日新聞の科学欄である。二十一世紀を専門家達が予想した記事の横に「究める」というコーナーがあって、そこに「女性の胸と男性の好みの進化的関係は?」というインタビュー記事があった。そして、その記事が蛍光ペンでマーキングしてあったのである。
これは一体、どういうことなのだ?と頭の中がグルグル&複雑な気持ちになりながら、とりあえずその記事を読んでみた。すると、この記事がとても面白い。インタビュー中の
ヒトは異性をどう選ぶのか?そんな疑問から女性のバストと弾性の好みに進化的関係があるかを研究している。という東大大学院の東海林さんの語りもとても面白いし、バストサイズを5段階に変えた女性の合成写真を使い、男子学生300人にアンケートしたという実験とか、巨乳好きの性格が父から受け継いだものであるかを調べるために、父子間で性的好みが伝達されるかを調べる、などの話もとても面白い。最高である。(中略)小さいバストほど魅力的だと母に教えられて育った。しかし、大きいバストが好きな男性がいることに気付いて驚き、「なぜ」と考えたのが研究のきっかけだった。(中略)「大きいバストが本当に普遍的に好まれるかを知りたい。控えめなバストが淘汰されてしまうとは考えたくないから」と話す。
そして、父からの封筒に入っていたもう一つの記事は宇宙科学研究所の新聞の中の宇宙基地利用研究センターの黒谷氏の「Anti-Gravity」というエッセイだった。なんでも、Anti-Gravityという化粧品があって、
それは顔の皮膚のコラーゲンに皮膚がたるまないようにするというものらしい。顔の皮膚にハリをあたえて、顔のたるみを防ぐのである。顔の皮膚のたるみ元をたどれば重力のせいだから、「anti-gravity= 無重力」化粧品ということになるわけだ。じゃぁ、このAnti-Gravityを体中に塗れば、バストやヒップが垂れるという女性の悩みもなくなるのではないか、と「無重力における生物の専門家」である黒谷氏は書いていて、参考文献に本サイトが挙げられていたのである。
うむむ、世の中には巨乳の科学について進化論的に研究している人がいたり、オッパイの力学について考え(てみたりもす)る無重力生活の専門家もいるのだ。これはマズイ。油断している場合ではない。私もオッパイ星人研究をもっと真剣にしなければならない。父はきっと私に「研究の厳しさ」を教えようとしたに違いないのである。私の父はこれまでの「オッパイ星人の力学」を読んで、美味しんぼの海原雄山風に「うわあっはっ、こんなものでオッパイ星人の力学だとは笑止千万!」位のことを言ったに違いないのである。
しかし、それだけではない。「二十一世紀、小さいバスト、大きいバスト、無重力、皮膚、オッパイのたれ」というヒントを与えてくれたのである。ここまでされて何かを書かなくて何としよう。オッパイ星人研究の手は一瞬たりとも休めてはならぬのである。そこで今回は「皮膚のハリ」や「重力」を気にしながら、「オッパイのたるみ・形状」について考えてみることにした。
さて、一体バストの形状というものはどうなっているのだろう?これまでの「オッパイ星人の力学」では
- 半球モデル
- 円錐モデル
そしてもちろん、このモデルに対して不満を持つのは私だけではなくて「これらのモデルには私は納得できません。」というメールがたくさん送られてきた。それどころか、「本当のオッパイをあなたは知らないのではないですか?」という実に失礼?なメールさえ送られて来ていたのである。「それでは、参考までに本当のオッパイの資料でも送って頂けないでしょうか?」とは私は大人なので返事をしなかったが、ちゃんとしたモデルを作らないことにはこれからもそんなメールがまだまだ来るに違いないのだ。
というわけで、今回は新しいバストの形状モデルを提唱してみたい。それは「バストの内部は液体に満ちていて、その液体を外側の皮膚が支える」という
- 水風船バストモデル
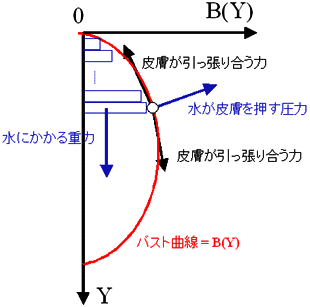
こんなモデルに基づいて、バストの形状を計算するにはどのように考えれば良いだろうか?次の図が「水風船バストモデル」における内部の水と各皮膚部分にかかる力を示してみたものである。これはバストの断面をを鉛直方向に示しており、左の黒い鉛直線が胸板であり、赤い線がバストの形状を示すバスト曲線である。(ちなみに、今回はバストを二次元の断面でのみ考えている。)
赤い線がバストの形状を示すバスト曲線
|
「水風船バストモデル」における内部の水には重力がかかり、バストの下の方にいくほど圧力がかかっている。そして、皮膚に面している内部の水はその圧力を皮膚に伝える。そして、皮膚はその圧力で変形しながら水で満ちたバストを支えるのである。この時、バストの形状= 皮膚の形状を示すバスト曲線はどんな条件を満たしているだろうか?
ここで、胸板にそって下向きにY軸をとり、バスト曲線をB(Y)で表すことにしよう。上の図をよく眺めるとわかると思うのだが、バストの形状= 皮膚の形状を示すバスト曲線をB(y)とすると、バスト曲線B(y)は実はこんな方程式を満たす。
 |
まぁ、ここでは簡単のために、係数を省略していたり、バストが本当に垂れてしまうような状況は考えていなかったりするので、ごく簡易的なバスト曲線方程式だと思って欲しい。大雑把に係数などを無視して、言葉で言ってしまえば、バスト曲線の傾きの変化はその点より上に位置するバストの重量に等しい、という感じである。自由境界におけるLaplaceの関係でも連想して頂ければわかりやすいだろうか?とにかく、この条件と適当な境界条件さえ入れてやれば、「水風船バストモデル」におけるバスト曲線B(y)は計算することができるのである。
さて、このバスト曲線方程式を一般化したり、係数をちゃんと計算したり、三次元に拡張したりということはまたいつか行うことにして、まずは適当にこのバスト曲線方程式を数値的に解いてみた。それが、例えば、次の図である。これが、「水風船バストモデル」のバストの形状の一例だ。
赤:すごくハリのあるヤングな皮膚の場合 |
この図の中でバスト形状のプロットが三種類あるのは「皮膚のハリ = 皮膚のヤング率」として三種類の値を使ってみたからだ。以前
の中でそう、もうお判りのはずだ。 「バストに関するヤング率」はまさにヤング率(Young率)なのである。実は年齢に比例する係数だったのだと書いたが、あれと同じである。今回は、年齢で変わっていくバストの皮膚のハリを「バストの皮膚のヤング率」とおいてみたのである。そういうわけで、皮膚のハリ= 皮膚のヤング率によってバストの形状は異なるわけだが、まずは眺めてみてもらいたい。以前のどうみても不自然な「半球バストモデル」等に較べて、ずっとましになっているとは思わないだろうか?特に、藍色・マゼンダのプロットなどかなり自然な形状になっていると思うのである。感受性の豊かなオッパイ星人であれば、必ずしやググッとくるハズである。
さすがに、メチャクチャ皮膚のハリがある赤色のプロットなどは松坂大輔もビックリの「超ロケット乳」になってしまっているが(といっても、この図のアスペクト比に意味はないんだけど)、今や時代は二十一世紀、宇宙へロケットで飛び出す時代だと思えば、こんな「超ロケット乳」を眺めるのもそれまた一興ではないだろうか。ぜひこの「超ロケット乳」には宇宙へ飛び出してもらいたいものである。
もちろん、世の中には「大きいことは良いことだ」という巨乳大好きオッパイ星人達もいるわけで、そんな人達のためにもう少し「大きいバスト」の場合で計算してみたものと並べて比較してみたのが次の図である。
 |
個人の好みもあると思うが、けっこう自然な「巨乳形状」が再現できている。ちなみに、今回使用した簡易的なバスト曲線方程式ではすごく巨乳だったり、皮膚のハリが無さ過ぎてあまりにバストが垂れている場合の計算はできない。簡単に言えば、Yに対してバスト曲線B(Y)が一対一対応しないためである。が、それゆえに巨乳と言っても美乳の範囲のみ考えることができるのである。
また、この「小さいバスト」の場合と「大きいバスト」の場合の比較から、「巨乳は垂れるのよっ!だから、小さい方が良いのっ!」という世の小振りなバストの女性がよく言うセリフの妥当性も確認してみたいところではなるが、そういうことは何か危険なことであるような気もしてきたので、今回は止めておきたい。
ところで、今回の話はAnti-Gravityから話が始まっているわけだが、ちなみに「水風船バストモデル」は無重力下ではどのような形状をとるかと言えば、当然体積に対して表面積が最小となる「半球形状」になる。つまり、「半球バストモデル」は「水風船バストモデル」の重力を無視した特殊な場合であり、逆に言えば「水風船バストモデル」は「半球バストモデル」にバスト内部での重力の影響を加えて一般化したものだったのである。
今回は、とりあえず新たに「水風船バストモデル」を提唱し、そのモデルにおけるバスト曲線B(y)を解くための簡易的な方程式を考察し、それを数値的に試しに解いてみた。次回は今回行った考察を用いながら、少し違うアプローチで「オッパイ星人の力学」を考えてみたいと思う。
さて、今回の話のきっかけともなった黒谷氏らの書いた本「星と生き物たちの宇宙」は原稿のごく初期の段階で実は読ませてもらっていた。その時感想を聞かれたときは、この本はメールのやりとりで構成されているので、「なるべく著者達の私的な部分を消さないままにしておいた方が面白いんじゃないか」なんて適当なことを言っていたのだった。その著者達が書いたこの本のあとがきの言葉を最後に引用して、これからの「オッパイ星人の科学」への「戒め」と「言い訳」としておきたい、と思うのだった…
科学は応用を通じて実生活に関わり、知的追求というこころの喜びにも関わる二面を持っています...多くの人に、こころを喜ばせる科学を楽しんでもらいたいですね。 H.Hirax, A.Kurotani
2006-08-20[n年前へ]
■続・西村和雄 教授に聞いてみたい経済学のこと 
「西村和雄 京大経済研究所教授へ質問してみたいこと」へのレスポンスなど。
「情報の伝達速度 vs 市場の安定性」 市場が微分方程式を離散的に積分しているとするならば、情報の伝達速度が速いほうが市場が安定するように思えます。けれど、現状は不安定に向かっているように見えるのは…なぜ?
「愚民ゆえの衆愚でなく、システムとしての衆愚」「神の見えざる手」「ビルトイン・スタビライザー」は、カオス・アトラクターとよく似たものなのでしょうか? そうであるとした時、(案外正しい?)「みんなの意見」「神の見えざる手」は時には物事を発散させてしまったりしないでしょうか?