1999-12-16[n年前へ]
■スキー場の特殊相対性理論 
ジャンプの飛距離は何メートルだ?
突然ではあるが、HIRAX.NETのドメインレコードを調べてみると、
Record created on 16-Dec-1998.となっている。自分のドメインのレコードをわざわざ調べたのは、一体いつ取得したのか私自身が忘れてしまったからである。何しろ、「できるかな?」は当初異なる場所での二本立てで公開していたため、私の記憶がごっちゃになっているのである。あと各回の公開順序も実はかなりシャッフルされている。そのため、完全に忘れていたのである。
「できるかな?」はHIRAX.NETのコンテンツの一部である。しかし、HIRAX.NETの誕生日よりも、「できるかな?」の誕生日の方が実は早い。
で書いたように、「できるかな?」はすでに満一年を迎えていたわけである。そしてやっと、本日でHIRAX.NETも満一歳になったわけだ。何はともあれ、目出度いことである。子供の頃やらされた「ドリル」でも3日も続かなかったのに、1年続くとは、正に奇跡である。奇跡はそうそう続かないような気もするが... さて、関係ない話はここまでである。今回の舞台は万座温泉だ。なぜなら、先週末私は万座温泉でスキーをしていたからだ。何故だか理不尽な話しではあるが、私は万座温泉でローレンツ収縮を考える羽目になったのだ。もう少し正確に言えば、スキー場で特殊相対性理論を考える羽目になったのである。(先に断っておくが、私はトンデモ話をマジメな顔で言うことが多い。)
 |
話の発端はスキーに行く前に遡る。職場の今年の新入社員であるタカノリ君(仮名)とスキーの話をしていた。彼は秋田出身であり、子供の頃からスキー三昧の生活をしていた。大学に入り京都へ行ってからは、スキーをやる頻度は下がったが、チョコチョコ行ってはいたという。
そのタカノリ君(仮名)と話していると、彼はさりげなくこう言った。
「10m位のジャンプはよくするスよ。」10mである。2mの身長の人の5人分である。それは、スゴイ。
「えぇ、本当かぁ〜〜」
「いやぁ、そんなのよくやることじゃないスか?」
今回のスキー&温泉旅行は職場(と何故か競合他社)の人達30人程で行った。ほとんどの人は、割にスキーは好きな人が多い。従って、スキーも上手い人が多い。その人達に囲まれながら、タカノリ君(仮名)は断言した。
「6,7mは簡単だけど、10mってスゴイなぁ。」タカノリ君(仮名)、ただ者ではない。
「本当かぁ〜〜」
「えっ、だってただ飛ぶだけじゃないっスか。」
そこで、スキー場でその確認をしたわけである。場所は万座プリンスゲレンデの下部である。リフトとコースが交差する辺りに、ジャンプできる場所があったのだ。そこで、彼は軽く滑り出し、力一杯ジャンプした。
果たして、タカノリ君(仮名)は何メーター飛んだのであろうか? それとも、ただのホラ吹き男爵であったのだろうか?
ところが、その答えをすぐに書くわけにはいかないのである。なぜなら、タカノリ君(仮名)がジャンプをしてみせた時に事件は起こったのである。
「どうスか!10mはいったんじゃないスか!」
「3,4mしかいってねーぞ!おイ!」
これは、一体どうしたことだろうか? しかも、会話はまだ続くのである。
「何でっスか!軽く1秒は宙に浮いてたっスよ!」ますます不思議なことに、時間感覚すら違っているのである。一体何が起こっているのだろうか?
「そんなことはねぇぞ!コンマ数秒だろう!」
私はここで気づいたのである。観測者の間で時間と空間の不一致が生じているのであれば、ここはもちろんアレの登場である。アレと言えば言うまでもない、もちろん特殊相対性理論である。
そう、万座温泉スキー場ではローレンツ収縮を実感することができるのである。「スキー場でジャンプする」という現象を考える際には、「スキー場におけるhiraxの特殊相対性理論」を導入しなければならないのであった。
それでは、簡単に「スキー場におけるhiraxの特殊相対性理論」を説明しよう。今回、生じている不思議な現象は以下のようになる。
登場人物
- タカノリ君(仮名) 速度vでジャンプをしている。
- 観客 静止している。
| タカノリ君(仮名) | 観客 | |
| 飛んだ距離 | 10 | 3 |
| 飛んでた時間 | 1 | 0.3 |
つまり、速度vで飛んでいるタカノリ君(仮名)の感じる空間や時間といったものは、静止している観客に比べて、いずれも3倍程度に膨張しているのである。
通常の世界で生じるローレンツ収縮は、速度vで移動している観測者の空間軸も時間軸も
![]()
倍縮むのであるが(ここでは光速c=1の単位系を使用している)、
であるが、「スキー場におけるhiraxの特殊相対性理論」では、速度vで移動している観測者の空間軸も時間軸も静止している観測者に対して、逆に![]()
倍に延びてしまうのである。もし、ミンコフスキーの時空図を書いて確認しようとする人がいるならば、座標軸の傾きの変化も通常のローレンツ変換と逆に考えてみてもらいたい(その延長で考えていくと、矛盾があるというご指摘メールはノーサンキューである。)。
さて、そもそもローレンツ収縮は、マイケルソン - モーリーの実験結果(エーテルの影響が検出できない)を説明し、なおかつエーテルの存在を認めるために立てられた。それは、「運動体はすべてその運動方向に収縮する」という仮説である。その仮説を理論的に完成させたのが、アインシュタインの特殊相対性理論である(考え方としては根本的に異なるが)。
今回の話の中で「エーテル」に変わるのは、「空気」だろうか? いや、違う。私はむしろ、速度そのものであると、考える。つまり、特殊相対性理論と同じである。スピードを出して飛んでいるという感覚、速度が与える感覚の変化、すなわち速度そのものが、「スキー場におけるhiraxの特殊相対性理論」を要請するのである。
今シーズン、スキー場でせっせとジャンプをする人がいるならば、ぜひ「スキー場におけるhiraxの特殊相対性理論」について考えてみてもらいたい。
このWEBへ来る人の中で、同時期に万座温泉スキー場にいた人はいるだろうか?12/11.12に万座温泉スキー場のプリンスゲレンデの下部でジャンプにいそしんでいたのが、私達の一行である。そして、その中の一人(ショートスキーでせっせと飛び跳ねていたヤツ)はこんなことをずっと考えていたのである。
さて、実際のタカノリ君(仮名)の飛距離がどの程度であるか知りたいと思う人も多いだろう。オマエらの主観的な評価でなくて、実測定した距離を教えろと思う人も多いに違いない。
「絶対的な基準など存在しないから、そんなことは私はわからない。」と言い放ちたいところだが、タカノリ君(仮名)の名誉のために書いておく。彼が飛んだ距離は、2m弱のスキー板で4本分はあった。実は、タカノリ君(仮名)の基準が一番正しかったのである。彼は、「やるときはやる有言実行の人」なのであった。
1999-12-21[n年前へ]
■恋の力学 
恋の無限摂動
クリスマスが近くなると、街のイルミネーションが綺麗に輝き始める。いかにも、ラブストーリーが似合う季節である。そこで、今回は、"Powerof love"、すなわち、「恋の力」について考えてみたいと思う。「恋の力」により、人がどのような力を受け、人がどう束縛されるのか、などについて考えみたいのである。また、恋に落ちたカップルがどのような行動をするのかについて解析を行ってみたい。
「できるかな?」では以前、
において、カップルが他のカップルを意識する力について考えたことがある。カップル同士の間に働く斥力を考えることにより、鴨川カップルの行動を考えてみた。それと同様に、今回はひとつのカップルのみを考え、その中に働く力を考えてみるのである。ひとつのカップルの「男」と「女」の間にどのような力が働くかを考えるのである。そういうわけで、今回の登場人物は「男」と「女」である。その二人は「恋に落ちた二人」である。二人の間には「恋の力」が働いているのだ。その二人の間に働く「恋の力」について考察することにより、恋に落ちたカップルの行動について考察を行ってみることにする。
といっても、「恋の力」を精密に測定した報告例は未だ存在しないので、ここでは適当な値を用いていくことにする。「恋は距離に負けない」とか「遠くて近きは男女の仲」などとははよく言われる。そこで、距離によらないと近似した。また、「遠くて近きは男女の仲」の意味を考えれば、恋の力は無限遠まで働く力である、と考えるのが自然である。
そこで、今回の「恋の力」は距離に関わらず一定であると仮定した。距離=rとした時に-r/Abs[r]の大きさで「相手に惹かれる」ものとした。仮に第一種「恋の力」(仮称)とでもしておく。
今回は「恋の力」は距離によらないものとした。しかし実際は、(通所の距離においては)「男」と「女」は距離が近いほど惹かれ合うし、離れてしまうと惹かれ合う力は弱くなるというのが自然であると思われる。そこで今回の第一種「恋の力」(仮称)は、あくまで大雑把な近似ということにしておく。
恋する二人の間に働く力をもう少し正確に記述しておくと、
- 「恋の力」 = - 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「恋の力」=優柔不断度 * 「恋の加速度」
であることだ。心がトキメいてもなかなか行動を起こすことが出来ない人がいるだろう。そういう人は「優柔不断度」が高いというわけである。恋の行動における慣性を示すパラメータである。
また、今回は空間を1次元であると簡略化してみた。1次元の空間の中で「男」と「女」が動き回るのである。その時間的変化を調べてみるのだ。従って、シミュレーション結果は空間軸が一次元+時間軸一次元で、合わせて2次元となる。
さて、この「恋の運動方程式」を解くことにより、恋する二人の行動は予測することが可能となるわけだ。試しに、その計算サンプルを示してみる。なお、今回は時間方向で数値的に逐次解を求めている。
初期状態は
- 「男」位置=5, 速度=0,魅力=100,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
位置や時間の単位は任意単位である。「0」と「5」は東京と大阪であっても良いし、ロンドンとニューヨークであっても良い。あるいは、実空間でなく精神的な空間と考えてもらっても構わない。すなわち、心の動きを示しているものとするのである。
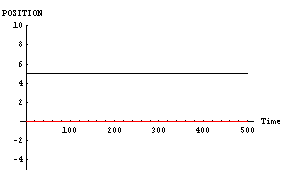
また、二人の「魅力」や「優柔不断度」は対等である場合だ。その結果を下に示す。このグラフは縦軸が空間位置であり、横軸が時間である。黒線が「男」であり、赤線が「女」である。
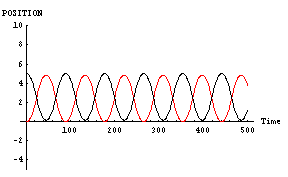 |
「男」と「女」が同じように相手の方向へ向かっているのがわかると思う。これが「恋の無限摂動」である。こういった「恋の無限摂動」の代表的なものには「君の名は」の主人公達の動きなどがある。恋に落ちた二人が、延々とすれ違いを続ける物語である。これは、この「男」と「女」の行動そのものである。
この計算結果では「男」と「女」が糸を紡いでいるようにうまく絡みあっているのがわかる。「恋の無限摂動」の幸せなパターン例である。これは、「男」と「女」が対等であったことがその一因である。
その証拠に、「男」と「女」が対等でない場合の計算結果を示してみる。次に示すのは、
- 「男」位置=5, 速度=0,魅力=10,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
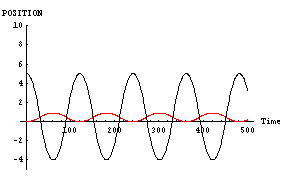 |
「男」が右往左往するのに対して、「女」はほとんど動いていないのがわかると思う。おそらく、この場合には「男」と「女」の「心」もこれと同様のパターンを示しているものと思われる。すなわち、「男」の「心」は揺れ動いているのに対し、「女」の「心」はほとんど動いていないのである。
先の例と異なり、これは実に不幸な計算例である。不幸ではあるが実際によくある例であると思う。以降、これを「男はつらいよ」パターンと呼ぶことにする。「女」に「男」が振り回されているパターンだ。もし、奇跡的に結婚などしても、将来どうなるかは火を見るより明らかである。
それでは、「男」と「女」の「魅力」が同等で、かつ、とてもスゴイ場合を示してみる。すなわち、ドラマの主人公達のようにとてつもなく魅力的な二人が恋に落ちた場合である。一般人とは違う二人が恋に落ちたら、果たしてどのような行動を示すのであろうか?この場合のパラメータは以下に示す、
- 「男」位置=5, 速度=0,魅力=1000,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=1000,優柔不断度=10
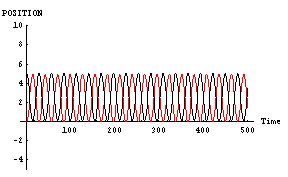 |
「魅力ある二人が恋に落ちた場合には、あまり近づかない方が良い」という教訓をここから得ることができる。
最後に、「男」と「女」の二人ともにあまり魅力がない場合である。パラメータとしては、
- 「男」位置=5, 速度=0,魅力=2,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=2,優柔不断度=10
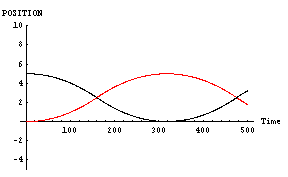 |
これなど「恋」と言えるのかどうかもわからない位である。ほとんど、「ただすれ違っただけの相手」である。これがさらに進むと、魅力がお互いに0同士のパターン、
- 「男」位置=5, 速度=0,魅力=0,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=0,優柔不断度=10
 |
これっぽっちも「男」と「女」は「恋」に落ちていないのである。これではカップルの「男」と「女」ではなく、単なる他人である。
さて、今回は行わなかったが、カップルに「恋のエネルギー損失」を導入することにより、「恋の無限摂動」を減衰させることができる。それにより、現実のカップルの行動にさらに近づくことができるのではないかと、私は考える。何らかの抵抗が生じることにより、「恋の無限摂動」が減衰するのだ。そして、二人は接近した状態で停止するわけだ。
さて、今回の登場人物は「男」と「女」だけであった。しかし、現実でも、ドラマの中でも、通常は多くの登場人物が登場する。登場人物が「男」と「女」だけというような理想的な条件のみではない。
人の恋路を邪魔する(主人公からすれば)ヤツも必ず登場する。また、特定の登場人物の間では斥力が働くだろう。そのような場合、一体どのような現象が生じるのだろうか。
そもそも、今回の恋する二人の行動パターンは予測可能であったが、現実そのようなことがあるだろうか?果たして、未来の行動パターンは予測可能なのだろうか?色々な登場人物が現れる場合にも、今回の結論は成立するのだろうか?
それらは次回の課題にしておく。題して、「恋の力学 三角関係編- 恋の三体問題- (仮称)」である。「恋の力」を一般化し、多体問題として解いてみたいのである。恋する人達とその周りの人達がどのような行動をするか、恋の三角関係においてどのような力が働いているのか、について解析を行ってみたい。今回は、そのための前準備というわけである。
1999-12-30[n年前へ]
■6502と並列計算とムーアの法則 
人間のクロック&スケールアップ
「物理の散歩道」を読み直していると、とある文章に興味を覚えた。
- 第五物理の散歩道 ロゲルギスト著 岩波新書
「通信を考える」の中の興味を惹かれた部分は「信号の伝わる速度と距離と処理速度の関係」を論じている部分だ。例えば、計算機は処理速度を高めるためには回路の大きさを小さくしなければならないとか、人間の頭脳の働きの速さから集団生活の広がりの限界について論じているのだ。例えば、
- 計算機の演算速度の時間スケール -> ナノ秒 = 10^-9s (クロックで考えると、1GHz)
- 人間の演算速度の時間スケール -> サブ秒 = 10^-1s (クロックで考えると、10Hz)
つまり、通信の速度が光速度であるとして、演算の単位クロックの間に通信が行われなければならないとするならば、計算機の時間・空間スケールと人間の時間・空間スケールは等しいだろう、という推論だ。
そして、さらにロゲルギストの想像は広がり、並列計算についても論じている。
計算機が東京と大阪に離れて置かれていて、通信をしながら作業をするとしたら、人間の場合にはそれと同じ条件というのはどんなものだろうか、と彼らは考える。それは、光の速度で55時間、ちょうど冥王星の軌道直径の5倍程度の空間スケールになる、と論じている。それ以上、離れた場合には演算の過程を共に行うのは無理ではないかというのである。
こういう文章を読んでいると、この文章が作られたのが30年以上前であることを忘れてしまいそうである。この人達の思索の自由さに憧れを感じてしまう。この人達は、頭の中にタイムマシンにでも持っているのだろうか、と感じてしまうのだ。
ところで、私がコンピューターをいじるようになった頃は、Apple][の時代だった。といっても、私はお金があふれていたわけではないので、XXX電子でAplle][のコンパチ基盤を買って組み立てて使っていた。その基盤上の6502は1MHzで動いていた筈だ(あぁ、I/Oの6809派vs6502派の論争が懐かしい!)。
それから20年程たち、CPUのクロックスピードは1GHzを越えようとしている。20年で1000倍である。そして、その集積度は、ムーア(GordonMoore)の法則の「半導体の性能と集積は、18ヶ月ごとに2倍になる」に従っている。
それでは、人間はどうだろうか?人間の脳味噌のクロックがどの程度であるか測定されているかどうか、素人の私にはよくわからない。しかし、WEB上のデータとしては、例えば
- Mayo's Profile( http://www.ceres.dti.ne.jp/~mayo/profile.html )
ロゲルギストの時代、すなわち30年以上前、から現在のMayo's Profileの値がほとんど変わっていないように、人間の演算スピードは変わるようなものではない。それは、そうだろう。ヒトのクロックスピードや集積度といったものは、変えるわけにはいかない。当然である。CPUと違ってプロセスルールを変化させるというような訳にはいかないのだ。
それでは、演算性能を上げようとしたらどうするだろうか?そうなると、並列計算を行うのが自然だろう。単独のCPUの性能を上げるわけに行かなくても、共同作業を行えば、演算性能を上げることができる。
現代はほとんどの作業が共同作業で行われる。また、その共同作業も大人数が関わるようになってきている。それは、どんな業種でも同じだ。一人では、なかなかできないことが多くなっている。
それら共同作業、すなわち並列計算、を行う人達(例えれば並列計算機における各ノード)を増やし、それらの間の情報転送をすばやく行うことが多くの作業(計算)を行うための手順だろう。
そこで、
で用いた- 人口増加( http://www.t3.rim.or.jp/~kabutoya/KABHTML/Yoi/2-1.html )
 |
なるほど、人間界の並列計算機におけるノード数は増加している。そして、各ノード間の通信速度を調べるために、まずは、
- 来て、見て、触って、情報伝達
- ( http://www.f-jhs.fukuoka-edu.ac.jp/3-3/jyoho.html )
西暦 内容これを全部転送速度に直してみる。といっても、よくわからない部分も多いので、私が適当に決めてみる。それでは、その変化を示してみよう。とりあえず、ここ200年位の間のものを考える。
-4000 のろし
-2400 伝書鳩
-2300 馬による伝令制度
1837 モールス電信機
1876 ベグラハム=ベル電話機
1909 グリエルモ=マルコーン無線電話機
1973 Ethernet XeroxPARCで生まれる。(ちなみにEther=エーテル)
1979 DIX規格=10Mbps
1992 FastEthernet=100Mbps
西暦 内容という感じだ。グラフにすると、
1837 モールス電信機 = 2bps
1909 グリエルモ=マルコーン無線電話機=10kbps
1979 DIX規格=10Mbps
1992 FastEthernet=100Mbps
 |
こんな感じである。対数グラフにおいて直線的に情報伝送速度が速くなっている。この関係は結構きれいである。
別に意図してこういう数字にした訳ではないのだが、不思議なことである。
このようにして、人間(ノード)間の転送レートが高くなることにより、先のような人口増加に伴うトラフィック増加をしのぐことができていると考えることもできるかもしれない。そして、人間達の共同作業、すなわち並列計算、を行うだけのバススピードを確保しているのである。
最近、会社組織などで分社化とか事業分割とかの話題をよく耳にする。こういった時に、分割における時間と空間のスケールはよく考える必要があるだろう。分割が有効なのは、ほとんど独立なものを分割する場合のみである。並列計算における領域分割などと同じだ。
共同作業がほとんどなく、結果のみをやりとりすれば良いような場合には分割による効果はあるだろう。その一方で、同じ事業・作業を行っているところが、離れていては作業の効率は上がらない。もし、技術系の会社でそのようなことを行うのであれば、事業や部署を並列化した際の真面目なシミュレーション位は行うべきだろう。いや、別に深い意図はないけど。
こういったことは「新・闘わないプログラマ No.109 時代錯誤」に書かれていることとも少し似ているような気がする。
さて、1999/12/30-2000/1/1は野沢温泉で温泉&スキーである。2000年問題で会社に泊まり込む人も多いが、私はスキー場で泊まり込みである。同時期に野沢温泉に行く人がいるならば、ぜひ一緒に「スキー場の特殊相対性理論」について討論したいと思う(スキー場で)。
2000-01-03[n年前へ]
■音場の定位を見てみたい 
立体音感を考える その2
前回(といっても間に他の話も挟まっているのだが)、
で「音の立体感」について考え始めた。今回はその続きである。「音の立体感」を考えるための道具を作る準備をしてみたい。色々なことを考えるには、その目的にあった測定器が必要である。何か新しいことをしようと思ったら、そのための新しい測定器を作成しなければならない(と思うだけだが)。そして、何より私は計測器なんてほとんど持っていない。だからといって、計測器を買うお金があるわけではない。というわけで、困ってしまうのだ。
そこで、立体音感を考えるための測定器を作っていくことにした。といっても、すぐにできるとも思えないので、色々実験をしながらボチボチとやってみることにした。勉強がてら、ボチボチやってみるのである。オーディオ関連のことにはかなり疎いので勉強にはちょうど良いだろう。
資料をいくつか眺めてみたが、特に
- 「立体視の不思議を探る」 井上 弘著 オプトロニクス社
- 音像定位の因子
- 両耳差因子 (音響信号)
- 音の強さ(振幅)の差
- 位相の差
- 周波数スペクトル因子
そこで、いきなりだが今回作成した解析ソフト「音場くん一号」のアルゴリズムは以下のようになる。
- PCのサウンド入力から、サンプリング周波数 22.05kHz、Stereo 各チャンネル8bitで取り込みを行う。
- 取り込んだデータを4096点毎にウィンドウ(Hamming or無し)処理をかける。
- 高速フーリエ変換(FFT)を行う
- FFTの結果の実部について、左右のチャンネルの差分を計算する
次に示すのが、「音場くん(仮名)一号」の動作画面である。「音場くん(仮名)一号」の画面構成は、
- 右側->制御部
- 左側->計測データ表示部
- 音声波形データ(赤=左、緑=右)
- 周波数(横軸)vs左右での音圧の差(縦軸)
- 時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)
 (黒字に赤、緑の色構成は変更の予定) |
計測データ表示部の拡大図を下に示す。
- 音声波形データ(赤=左、緑=右)
- 周波数(横軸)vs左右での音圧の差(縦軸)
- 時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)
この表示計の意味を例を挙げて説明したい。例えば、下の画面では左の方に定位している音が鳴ったときの状態を示している。一番上の音声波形データでは緑(右)の波形は小さいのに対して、赤(左)の大きな波形が見えている。
また、真ん中の「周波数(横軸)vs左右での音圧の差(縦軸)」では横軸100(任意単位)程度の高さの辺りで左チャンネルに位置する音が発生しているのがわかる。
また、一番下の「時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)」では時間的に一番最後(横軸で右側)の方の横軸560、縦軸100位の位置に白い(すなわち左チャンネルに定位する)音が発生しているのがわかると思う。
 |
この曲のイントロでは、「ポンッ」という音が高さを変えつつ、左右にパンニング(定位位置を変化させること)する。
一番下の「時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)」を示したグラフ中で白・黄色(左に定位)と青・黒(右に定位)する音が時間的にずれながら現れているのが判ると思う。
このようにして、この「音場くん(仮名)一号」では音の定位状態についての「極めて大雑把な」計測が可能である(保証はしないけど)。「音場くん(仮名)一号」を使った他の例を示してみる。
下は種ともこの「O・HA・YO」の中から「The Morning Dew」のイントロ部を示したものだ。
- 左(白・黄)チャンネル方向に定位するピアノ
- 右(黒・青)チャンネル方向に定位するガットギター
 |
これはまるでオルゴールのピンを見ているようだ。あるいは、シーケンサーや昔の自動演奏ピアノのロール譜のようである。対位法などの効果をこれで確認したくなってしまう。
さて、ここまでの例は楽器も少なく、比較的自然な定位状態であった。しかし、以下に示すような場合には不自然なくらいの「音の壁」状態の場合である。かなり状態が異なる場合だ。
 |
これは、種ともこの「O・HA・YO」の中から「KI・REI」のラストのラストコーラス部を示したものである。人のコーラスが重なり合っていく部分である。色々な高さの声が重なり合っていく様子がわかるだろう。
ところが、このグラフをよくみると、同じ音が時間的に持続しているにも関わらず、時間毎に定位位置が左右で入れ替わっているのがわかる。
これはきっとエフェクターで言うところのコーラスなどをかけたせいだろう(素人判断だけど)。人工的にフィルタ処理をしているためにこのようになるのだろう。こういう結果を見ると、「音場くん(仮名)一号」をプログレ系の音の壁を解析してみたくなる。
さて今回は、音声の定位状態を解析する「音場くん(仮名)一号」を作成し、いくつかの音楽に対して使ってみた。まだまだ「音場くん(仮名)一号」は作成途中である。これから続く立体音感シリーズとともに「音場くん(仮名)」も成長していく予定である。
さて、一番先の画面中に"Re"という選択肢があるのがわかると思う。もちろん、これと対になるのは"Im"である。FFTをかけた結果の"実部"と"虚部"である。"実部"の方が左右の耳の間での音の大きさの違いを示すのに対して、"虚部"の方は左右の耳の間での位相差を示すものだ。つまり、ある周波数の音が左右の耳の間でどのような位相差を示すものか、測定しようとするものである。
左右の耳に対する音の位相差というものは、立体音感を考える上では避けては通れないのだろう。しかし、位相差を処理しようとすると、どうしたらいいものかかなり迷う部分がある。また、今回のようなFFT処理をかけたときに得られる位相を用いて良いものかどうかもよくわからない。というわけで、今回は位相解析処理は後回し、ということにした。
2000-01-31[n年前へ]
■落ちゆくエレベーターの中…で悩みます? 
無重力の理想と現実(仮)
今日もまた「ちゃろん日記(仮)」を読みに行くと、何とも面白い話があった。
である。この「ちゃろん日記(仮)」は「疑問とそこに隠れている真実を見つけだす感覚」に満ち溢れている、と私は思うのである。面白すぎである。さて、今回の話は、エンパイアステートビルでエレベーターが落ちたっていうけど、落ちていくエレベーターの中の人は
- 床に張り付く
- 天井に張り付く
- 宙に浮かぶ
「ほんとう〜にそうか? ほんとう〜にそうか?」
こういういかにも教科書に載っていそうな話には、時として落とし穴がある。教科書に書いてあるのは理想的で単純化した場合の結果である。それを鵜呑みにすると間違えてしまうことになる。極端に言えば、教科書に書いてあるような理想的な状態はほとんど存在しないので、教科書に書いてあるような現象はそうそう再現しない、ということになる。
ピサの斜塔から「落下の実験」を行ったのはガリレオ・ガリレイであると思っていると間違いである、というのは少し違う例になってしまうか。
久しぶりに思い出したが、私の所属していた研究室では重力測定は大きな柱であった。そして、確か大学院の入試問題の内の一題は、まさに
「落ちていくエレベーターの中の人達に働く力を精密に論ぜよ」であった(簡単に大雑把に言えば)。私はちゃんとこの問題を解けた覚えがない。いや、はっきり言えばずいぶん悩んだ覚えしかない。ってことはいまいち解けなかったのだろう。なので、「落ちていくエレベーターの中の人達は無重力状態である」と聞くと、「ほんとう〜にそうか? ほんとう〜にそうか?」と歌いたくなる。
研究室関連では、絶対重力測定を行う研究をする人達もいたわけである。絶対重力(加速度)測定は自由落下する物体の運動を測定して、重力加速度を測定するわけであるが、そう簡単に物体は自由落下してくれないのである。簡単な実験で物体を自由落下させて重力加速度を測定してみるとわかるが、大雑把な実験(自分の家ですぐできる程度の)では一桁ちょいの精度しか出ない。一桁ちょいの精度しかでないということは、(例えば)体重が10%弱程度になったように感じるかもしれないが、それは無重力ではない。体重が60kgの人であれば、6kgも感じてしまうのである。(雑な話だが。)
空気中を落ちてくる雨だってそうだ。もし、雨が自由落下を続けていたらものすごいスピードになって、雨に打たれるのは命がけになってしまう。しかし、実際にはそんなことはない。空気抵抗で速度は飽和してしまい、自由落下状態ではないからである。
さて、本題である。果たして、
例えば、
- 若井研究室の研究概要
- http://mech.gifu-u.ac.jp/~wakailab/research/Basic/base_h.html
北海道の上砂川町にある施設(JAMIC)で、490m落下させることにより、10秒の無重量環境が得られます。落下中は空気抵抗を受けるので、落下カプセルを二重構造にし、空気抵抗を無視できるように工夫してあります。と、記述されているように、実際には工夫をこらさなければ無重力状態は実現できないのである。絶対重力系などでも空気抵抗を無視するために、投げ上げて往復運動を測定するなどの工夫がいるのである。
と、言葉だけで書いてもしょうがないので、適当な計算でもしてみる。いや、もちろん、実験をするのが良いわけであるが、面倒だし…
まずはエレベーターには、
- 何の抵抗も働かない
- 空気抵抗とワイヤーの抵抗が働く
そして、エレベーターの中の人には空気抵抗は働かないとした。エレベーターの中の空気と人の速度差はほとんどないからである。また、エレベーターは人よりもはるかに重く、人の重さはエレベーターの運動に何の影響も及ぼさないと近似した。
その計算の結果を以下に示す。これが落ちていくエレベーターの軌跡である。抵抗のない場合が(赤)で抵抗のある場合が(青)である。エレベーターが落ち始めてから30秒後までの軌跡である。
 |
理想的な場合(赤)に比べて、抵抗のある場合(青)の落ち具合が鈍っているのがわかると思う。それでは、もっと時間が経った場合はどうだろうか?それを次に示す。エレベーターが落ち始めて300秒後までの軌跡である。つまり、五分間もこのエレベーターは落ち続けているのである。落ちた距離は理想的な場合で40kmの深さに達している。すごいエレベーターである。こんなに落ち続けていると、すでに重力加速度が一定とは言っていられなくなる。
 |
ここまでくると、抵抗のない場合(赤)と抵抗のある場合(青)では全然違う軌跡になっている。抵抗のない場合(赤)では放物線そのものであるが、抵抗のある場合(青)では一定の速度になっている。
それでは、エレベーターがこのような状態になった時の、エレベーターの中の人に働く加速度(と実際の加速度の差分)を示してみる。これを見れば、落ちていくエレベーターの中の人が無重力状態であるかどうかがわかる。まずは、300秒後までの変化を見てみる。
 |
理想的な場合(赤)はずっとゼロすなわち無重力状態であるが、抵抗のある場合(青)は無重力状態は最初だけで、50秒後位には通常の状態に戻ってしまっている。最初の部分をもう少し拡大してみる。次に示すのは、3秒後までの落ちていくエレベーターの中の人に働く重力加速度(と実際の加速度の差分)である。
 |
これを見ると、あっという間に人は無重力状態ではなくなっているのがわかると思う。
というわけで、先の三つの選択肢、
- 床に張り付く
- 天井に張り付く
- 宙に浮かぶ
先日みたニュースのエレベーター落下実験の中で、中にいた男性リポーターが、落下しながら「ひぃ?」とアオ向けになった状態で床にハリ付いていたからなのです。という実際の現象が正しいのである(いや、もちろん状況はかなり異なるが)。「頭の中だけ」で考えたことというのは大抵の場合間違ってしまう。(もちろん、今回の「できるかな?」の話もその例外ではない)
そして、その後に、
ありはきっと、速度がそこまで充分でなかったのと、もしやのトキのために、男性リポーターに安全な姿勢をとらせていたタメだと思われます。とあるが、実際問題として「速度がそこまで充分」になることは未来永劫ないわけである。だから、(私の中では)エレベーターの中の男性リポーター氏は床から浮かぶことはないのである。
こういうのは、結局考える人の数だけ答えがあるのだと思う。もし、その内のどれが真実に一番近いかどうか知りたければ、実験すれば良いだけの話だし。