2002-08-26[n年前へ]
■CleType自主学習（仮） 
ちょっと真面目にClearType（仮）
(2002.08.26〜)
- 楽しそうな「iMac」＆「電子ブック」風ノートPC用スタンド -はじまり - (2002.08.26)
- 一本道か、分かれ道か - ドキュメントの縦横比について- (2002.08.29)
- 水平思考と垂直思考 - 文字の縦横解像度 - (2002.08.29)
- 細かくすると楽（粗く）になる？ - ClearTypeの一番の秘密- (2002.09.09)
楽しそうな「iMac」＆「電子ブック」風ノートPC用スタンド -はじまり - (2002.08.26)
Lapvantageという楽しそうな会社を初めて知った。ノートPCをiMac風にするLapvantageDomeやPCを縦置きで使うためのLapvantagePortraitという、とても実用的でいて、それでいて明和電機のような面白い製品を作っている会社である。明和電機は兄弟が運営しているが、こちらのLapvantageの方はビアボーム親子がやっているらしい。iMac風スタンドの方は角度が振れないようのが（特にノートPCを立てられない）残念だが、Lapvantageの方はもう少しデザインがスマートであるならば今すぐにでも欲しくなる。
 |  |
複数の作業を切り替えながら作業をしたり、あるいはツールバーが多数出てくるようなソフトウェアを使って作業をする時には、左右に広いディスプレイが便利で使いやすい。しかし、単純に一つのドキュメントを読んだり、一つのドキュメントを書いたりする場合には上下に長いディスプレイを使うと、見通しがきいて考えをまとめやすくなる。気のせいか、頭の中の見通しがとても良くなるように感じたりする。だから、以前から横長の画面のノートPC(ToshibaPortege 320)を愛用していたりした私はノートPCの画面を横にして使ったり、縦にして使ったりと、画面を切り替えて使ってみたいと感じていた。AdobeAcrobat Readerであれば、画面を回転させて文章を読む機能があるので、これまでノートPCを回転させて電子ブックのようにして文章を読んだりすることもあった。
Lapvantage PortraitはPivotProのソフトウェア付きなので、Windowsの画面を自由自在に回転させることができる。だから、ノートPCを普通に横置きに使ってみたり、スタンドに載せて縦置きに切り替えて使ってみたり、と好きなように切り替えることができる。「これはなかなか便利そうだ」と思い、私も私も30日有効のPivotProのデモ版をインストールして使ってみることにした。
そして、このソフトのインストールをきっかけにして
で調べたClearTypeに関して、ちょっと少し考えてみた。 （続く）一本道か、分かれ道か - ドキュメントの縦横比について- (2002.08.29)
前回書いたように、複数のことを考えるなら「左右に長いディスプレイ」が良くて、一つのドキュメントを読むなら「上下に長いディスプレイ」が良い。その理由を端的に言えば、「目が左右についているから」だと思う。
まず、「目が左右に付いているので、あまりに大きい左右への目の動きは、目にとってとても非対称な作業であるから不自然」だ。だから、左右を眺めるときには自然と頭を左右に振ることになる。その頭を左右に振るという作業は、頭の中での何らかの切り替え作業を伴うような気がする。だから逆に、ツールパレットの切り替えのような「何らかの作業の切り替え」を伴う作業であれば、その左右へ視線を移動する（自然と頭も左右に動かす）ということはとても自然な行為になる。しかし、それは一つのドキュメントを読むような場合には、いたって不自然な行為になってしまう。だから、一つのドキュメントというのは本来「上下に長い＝縦長」であるべきだと思う。
そしてまた、「目が左右についているから」、人は上下方向を「一本道」に繋げて考える。例えば、絵画を眺めるとき、上に見える景色は多くの場合遠い景色で、下に見える景色は多くの場合近い景色だ。漱石の文学論の図を引くまでもなく、この「上下の遠さ、距離」というものを例えば時系列上の「一本道」に繋げるのは、いたって自然な連想だと思う。「遠い上」に見えるものは「遠い過去」で、下に来ればくるほど新しいことになる。それは、ドキュメントを読む場合に対応させて考えると、とても自然だ。それに対して、左右に並ぶものは決して「一本道」ではないのである。それは、「選択肢＝分かれ道」であって、決して一つの道ではないのである。左右に並ぶものは「複数の何か」なのである。
だから、一つのドキュメントは上下に並び、上下に長いべきなのである。ドキュメントの表示も同じく、縦に長いべきなのである。
 漱石 「文学論」より |
最近のPCであると、ディスプレイは通常横に長い。だから、本来縦に長くあるべきドキュメントを眺めようとする場合には、表示を90°回転させてやることもある。そうすると、本の一ページのようにして画面表示を眺めることができる。例えば、AcrobatReaderで表示画面を回転させたり、PivotProなど使ってPCの画面表示自体を回転させてやれば良いわけである。
 |  |
 |
このように、ドキュメント表示のための縦横比については、単にディスプレイの表示を90°回転させてやれば問題は解決する。しかし、表示のためのもうひとつの条件、表示品質が問題になってくる。そもそも、液晶(二十世紀においてきたCRTは無視しよう)の解像度はまだま低くて、それを改善するための技術としてClearTypeやCool Fontがあるのだけれど、AdobeのCool Typeはともかく、Clear Typeの場合には表示が90°回転しているという情報をClearTypeが取り扱わない（知らない）ために、上手く動かなくなってしまう。ClearTypeにしてもCool Fontにしても、液晶のRGBのカラーフィルターの並び方を利用してやることで解像度を高めているわけで、その並びの変化（表示の回転）に対応できない場合には表示品質を大幅に落とすことになってしまう。
次に、「ファイト！縦文字文化 -縦と横の解像度を考えよう - (2001.04.29)」で考察した、文字の解像度についてもう少しちゃんと考えてみることにする。
水平思考と垂直思考 - 文字の縦横解像度 - (2002.08.29)
ドキュメントを表示させるためには、文字を表示させてやらなければならない。しかし、液晶ディスプレイの解像度は必要十分には高くないから、文字はつぶれてしまうことが多い。例えば、「現実問題春夏雪雹資本主義電計算機」なんて文字を表示させてみるとかなり潰れてしまい、非常に読みにくいのが判るはずである。これが、英語の"RealProblem seasons Snow capitalism Computer"なんて文字であれば、まだマシである。
この日本語と英語の文字の解像度の差について考えてみる。比較例は下に示した、「漢字」と「英語」のテキストを用いることにする。
 |  |
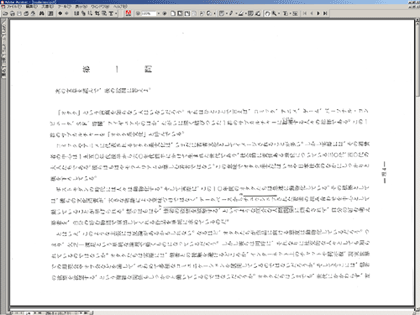
まずは、600dpiで20ptのMS Pゴシックのフォントを展開して上のような画像にした後に縦・横方向のそれぞれの解像度を考えてみる。ここでは、縦・横方向の黒い線（あるいは線でない部分）の太さ（幅）の分布を測ってみることにした(今回解析のために作成したソフトはここ（RunLength.lzh）においておく)。テキストのような二値の画像の「解像度特性」を計測するのであれば、このような解析にしなければならない。「ファイト！縦文字文化 -縦と横の解像度を考えよう - (2001.04.29)」でやったようなフーリエ解析は適切な方法ではないのである。
下の図が縦・横方向の黒い線（あるいは線でない部分）の太さ（幅）の分布である。縦方向に計測した黒い線（あるいは線でない部分）の太さというのは、結局のところ横線の太さ（あるいは線の間隔）であり、横方向に計測した黒い線（あるいは線でない部分）の太さというのは、結局のところ縦線の太さ（あるいは線の間隔）ということになる。どれだけの細かさで「太さ」（あるいは「位置」）を描いてやらなければならないか、を示すグラフということになる。
 |  |
「漢字」の場合には「Vertical 方向で計測した線の太さ（あるいは線の間隔）、すなわち横線の太さ（あるいは線の間隔）」が「縦線の太さ（あるいは線の間隔）」に比べて、大きく小さい方にシフトしていることが判ると思う。また、横線の量が縦線の量に比べてずっと多いことも判ると思う。後者は「数字文字の画像学 -縦書きと横書きのバーコード - (2000.01.21) 」で考えたことと全く同じで、「日本語は横線が多い」ということを端的に示している。そして、前者は「Vertical方向で計測した（すなわち横）線の太さ（あるいは線の間隔）」が縦のそれより大幅に小さいということは、「漢字」の解像度は縦方向に大幅に解像度が高い、ということを示している。漢字は縦書き文字故に鉛直思考志向なのである。
一方、「アルファベット」の場合には、これも「数字文字の画像学 -縦書きと横書きのバーコード - (2000.01.21) 」で考えたことであるが、縦線と横線の量においてはむしろ縦線の方が多いことが判る。水平方向に対して情報量が多いのである。アルファベットは水平思考志向なのである。「アルファベット」の情報量はそのかなりの部分が縦線によるものなのである。そしてまた、線の太さ（あるいは間隔）は横線の方が細い（あるいは線間隔が短い）が、その横線であっても「漢字」の縦線程度の解像度であることが判る。「漢字」に比べて「アルファベット」の解像度は低いのである。
ただし、文字の解像度を「線の太さ（あるいは間隔）の最小値」だけで論じることはできない。「適切な線の太さ（あるいは間隔）」にすることができるほどに解像度が十分高いか、ということも重要である。もし、そうでなかったら線が妙に太くなったり、細くなったりしてしまったり、あるいは、線の間隔が妙に近づいたり離れてしまったり、つまりは文字のプロポーションが崩れてしまったりするだろう。上の場合は600dpiで文字を表示させた場合の解析例だが、次に現在の液晶と同じような解像度（例えば）150dpiでこの文字を表示（展開）させてみる。こうすることでことで「適切な線の太さ（あるいは間隔）」にできていない様子を確認してみたい。
細かくすると楽（粗く）になる？ - ClearTypeの一番の秘密- (2002.09.09)
まずは、「現実問題春夏雪雹資本主義電計算機」という漢字と"RealProblem seasons Snow capitalism Computer"というアルファベットを現在の液晶と同じような解像度（例えば）150dpiでこの文字を表示（展開）させてみた。そして、前回と同じようにそのビットマップ画像の「縦・横方向の黒い線（あるいは線でない部分）の太さ（幅）の分布」を調べてみる。その結果が下のグラフである。また、前回に調べた、これよりも４倍程解像度が高い「600dpiで20ptのMSPゴシックのフォントをビットマップに展開してみた場合」をさらに下に比較用として示してみる。
 |  |
| |
150dpiでTrueTypeをビットマップに量子化した場合には、漢字・アルファベットの場合共に、縦・横方向とも600dpi単位で4,8pixelの太さ＝150dpiで1,2ピクセル幅のパターンが発生していることが判る。このようなパターンは、600dpiで20ptのMSPゴシックのフォントをビットマップに展開してみた場合には見られなかったものである。つまり、、着目すべきは例えばアルファベットの場合、
- 縦方向には幅10pixel(600dpi単位)=2.5pixel(150dpi単位)以下の高い周波数は存在していなかった
- 横方向には幅13pixel(600dpi単位)≒3pixel(150dpi単位)以下の高い周波数は存在していなかった
- 縦・横方向共に幅4,8pixel(600dpi単位)=1,2pixel(150dpi単位)以下の高い周波数が生じている
- 縦方向には幅7pixel(600dpi単位)≒2pixel(150dpi単位)以下の高い周波数は存在していなかった
- 横方向には幅11pixel(600dpi単位)≒2.5pixel(150dpi単位)以下の高い周波数は存在していなかった
- 縦・横方向共に幅4,8pixel(600dpi単位)=1,2pixel(150dpi単位)以下の高い周波数が非常に多く生じている
また、これらの文字の場合には本来18〜15≒12pixel(600dpi単位)の線幅・線間のパターンが多いわけであるが、それを150dpi単位（ =600dpi単位で4pixel )で量子化してしまうと、場所により4/12 = 33%もの線幅・線間の位置の誤差が生じてしまうことになる。不必要に狭い幅のパターンが作成されたり、不必要に広い幅のパターンが作成されたりして、これでは文字の線が太くなったり細くなったり、線の位置が狂ったりしてしまい、見にくいことこのうえない。これはすべて、150dpiという低解像度で量子化してしまったためである。「低解像度の表示系の解像度に合わせて量子化（ビットマップ化）してしまうと、ますますその表示系では表示しづらい高周波のパターンが生成されてしまい、結果として読みづらい」という一見逆説的に思えてしまう（しかし当たり前の）現象が生じている。
ところで、本題のClearTypeの場合には横方向（通常の液晶はRGBの3つのサブピクセルが横方向に並べられているから）の解像度を3倍だと仮想的に考えて、横方向を3倍の解像度で量子化を行うことになる。ここで、話の単純のために3倍≒4倍と思うことにすれば、つまりはClearTypeの場合には本来150dpiの解像度であるにも関わらず、サブピクセルを考えて600dpiの解像度で量子化している、ということである。それは結局上の二つのグラフの比較と同じであって、ClearTypeを使うと実は表示すべきパターンが「より表示しやすい低い周波数のパターン」になっているのである。それは、「文字の線が太くなったり細くなったり、線の位置が狂ったりしてしまう」ことがなく、目にとってはとても見やすいパターンになるだろう。この量子化の段階について触れている情報は見たことがないが、実はこの量子化の段階にClearTypeの隠された（しかし、一番重要な）メリットがあるように思う。また、アルファベットの場合にはHorizontal方向に振幅を持つパターン（＝縦線）が支配的に多いため、Horizontal方向に仮想的に高解像度の量子化を行うことは非常にメリットを効果的に得られると考えるのが自然である。
次に、このように量子化されたデータをClearTypeで表示する際の問題点・その解決方法について考えてみていくことにしたい。
P.S.ちなみに解析ソフト（RunLength.lzh）をアップロードしました。
2003-02-02[n年前へ]
■モーニング娘。でクラスタ分析
グラフ理論で今日からあなたもプロデューサー
昔からワタシには「手を抜くために色々とクダラナイことをする」という悪い癖がある。しかも、そのクダラナイことをした結果、必ずと言っていいほどに結局のところ苦労が増えまくるという結果になるのである。いわば、ドラえもんの「のび太」がいつもドラえもんの便利な道具に頼り、しかもその道具にしっぺ返しを必ず受けてしまうのを地でいくタイプなのであった。いつも、ワタシは手を抜くための道具を色々と作り、そして必ずそのしっぺ返しを食っていたのである。いわば、ドラえもんののび太とドラえもんを一人二役でマッチポンプのように演じ続けてきたのがワタシのこれまでの人生だったのである。
最初に記憶に残っているそんなワタシの悪い癖は小学生の頃のことだ。生徒会か何かでワタシは募金の集計をしなければならなかったのである。1000人を遙かに超える生徒がせっせと集めた募金なのだから、硬貨にしても膨大な枚数だった。といっても、ほとんどは一円玉とか10円玉だったのだから、それほどの金額ではなかったのだろうけれど、とにかく膨大な枚数だったのである。
そこで、ワタシは「ここは硬貨の重さを量って、金額を計算してみるのはどうだろうか？」と提案してみたのである。各硬貨の一枚当たりの重さは判っているわけだし、各硬貨に分けた上で全部の重さを量ってそれで金額に換算しちゃえば楽じゃないの、と提案してみたのである。ゼニ勘定に疲れていた周りの人々もその提案に喜び、「重さの誤差はどのくらいあると思う？」などとガヤガヤと計算しながら、みんなでせっせと硬貨を袋に入れて重さを計り始めたのである。
そして、机の上に重さを量り終わった硬貨の袋が何袋も並ぶ頃、そんな小さな銀行泥棒たちが盗んだお金を袋に入れてる最中のような様子を小学校の先生が発見してしまったのである。そして、当然のごとく私たちは先生にこっぴどく怒られたのである。「みんなが苦労して集めたお金のありがたさが判っていない」と当然のおしかりを強く強～く受けたわけである。「算数の問題解いてるんじゃぁないんだから！」とこっぴどく怒られたわけなのである。結局、私たちは硬貨の袋から硬貨を取り出して一枚一枚数え直すことになったのであった。もちろん、他の人をそそのかしたワタシに対する周りの視線は非常にキツく、ワタシの疲れも倍増したのであった。最初から硬貨の数を数えた方がよっぽど楽だったのである。
大人になってしまったワタシは今だにそんな「手を抜くための道具」を作り、そしてしっぺ返しを食らい続けている。三つ子の魂百まで、というわけなのであるが、今回は少し前にやってしまったそんな失敗を反省を含めて書いておこうと思う。
ワタシは仕事の上で色々な調査をしなければならないことがある。例えば、他のライバル会社がどんなことをしているかとか、あるいは、もっと詳しくライバル会社の中の人たちがどんな風に繋がっているか、とかを調べなければならなかったりすることがある。色々な発表資料を読んだり膨大な数の特許を読んだりして、そこに登場してくる人たちの関係を調べて、色々な推定をしていかなければならない。そのためには、たくさんの書類を調べなければならないわけで結構これがシンドイ作業なのである。
で、ワタシはこう考えたのだった。数百件もあるいは数千件も色々なものを読んで、その中に登場する人たちの関係を推定するなんてツライから、「たくさんの文書を勝手に読んで、勝手にその文章からライバル会社の中の人の関係を推定するソフト」を作っちゃえ～、と思ったのである。手を抜くためのクダラナイことのためには、苦労をいとわないワタシはそんなゴリゴリゴリゴリ真面目にそんなソフトを作ったのであった。「たくさんの文章の作者を調べ、その共著の関係から著者間の関係を調べる」というそんなソフトをせっせと作ってみたのである。そして作った後は、もちろんソフトのテストをしてみよう～、ということになった。
じゃぁ、そのサンプルデータは何を使ってみようかなと考えている時に、頭の中のどこかでモーニング娘。の「ここにいるぜぇ！」が流れ始めたのである。そこで、ワタシはモーニング娘。を含むハロープロジェクトを他社に見立てて、これまでに発売されたCDに参加している頻度・関係性等から、ハロープロジェクト内の「それぞれの人の配置」を調べてみることにしたのであった。
というわけで、つんく率いるハロープロジェクト関連で発売されているCDの枚数(なんと80枚以上だ!)に驚きながらも、CDに参加しているメンバーのデータをソフトに流し込んで、適当な各メンバーの関連性を示す数値を計算した上で、まずは各メンバーを近いものに分けるために、クラスタ分析してみた。ここで、解析ソフトは各CDに誰が参加しているかだけを知っていて、「モーニング娘。」とか「タンポポ」とかのグループが結成されていることは知らないのであるが、とにかくハロープロジェクトの中の各メンバーの「組織図」が判るわけだ。（ちなみに、ここでは似通ったものを樹形図（似通った度合いを示すグラフ、会社で言えば組織図みたいなもの）として表示するために、「Excelアドイン工房」のクラスタ分析アドインを使っている。）
まずは、前半41作のCDから推定したハロープロジェクトの中の各メンバーの関係性を示したのが下のグラフである。
 |
この樹形図グラフを眺めれば、（CDのカップリングから判断される）で誰と誰が結構近い関係にあるか、というようなことが判るハズである。といっても、このグラフでは色々なメンバーが参加したアルバムもあるいは一つのグループだけが歌うシングルも同じ重みで計算していたりするので、モーニング娘。あたりのファンの感覚からは大きくずれるかもしれないけれど、とにかくこんな「組織図」が計算されるのである。
上の前半41作から計算した樹形図の方は結構シンプルなものなのだけれど、次に示す後半41作のCDから推定した後半41作のCDから推定した各メンバーの関係性の方はもう少し複雑だ。組織的にライバル会社ハロープロジェクトは前半より複雑になってきているのである。
 |
こんな感じで、他社（ここではハロープロジェクトをそれに見立てたが）の発表資料（特許とか製品報告とか）からこんな各メンバーの組織図を示す解析ソフトを作ってみたわけなのだけれど、これではどうも不十分なのである。どうしてかといえば、各メンバーの結びつきがこの樹形図ではどうしても判りにくいのである。こんな風に各メンバーが一次元に並んでいる図ではどうも今ひとつ判らないことも多いのである。そこで、ワタシはさらに「各メンバーの結びつきを示す二次元グラフ」を出力することにしたのである。誰と誰がどのくらい近い関係にあるかなどを判りやすく表示させてみたのだった。そんなサンプルを少ないデータで表示させてみたのが下のグラフだ。モーニング娘。のメンバーの関係が判りやすい？グラフになっているのが判ると思う。
このグラフ上で各メンバーを動かせば、「飯田をこっちへ持っていけばどうなる？あー、安部がそっちへ行っちゃったよー。どうするー？」というような具合で、各メンバーの配置やプロジェクトのメンバー編成などを実験することができるのである。グラフ理論で今日からあなたもプロデューサーなのである。グラフぐりぐりで、今日からあなたもつんくなのである。グラフ配置で誰でもつんくの気持ちになれるのである。
という感じで、ソフトのテスト（になっていたのだろうか？）を終えたワタシはライバル会社の組織図を作ったのである。で、それを使いながら「この人たちはきっとこんな感じの組織になっているんですよー。そして、こんな感じでその組織は変化していったんですよー」なんて報告をしたのである。すると「おぉー、これは結構使えるかもー、なかなかスゴイぞー」となかなかに良い反応だったのである。
そこで、さらにワタシは調子に乗って「ライバル会社の各メンバーの結びつきを示す二次元配置グラフ」の方で「この人をこっちに近づけるとこの人がこっちへー、これがライバル会社の人間関係なんですよー、ほらほら～」と見せたりすると、もうこれが「おぉぅ…？ …これは何て言ったら良いのかなぁ…？スゴイ…んだけどなぁ……」と逆効果どころじゃなくもう引きまくりだったのである。そして、引いてしまった引き潮をもうどうにもすることもできないままに、結局そのグラフはお蔵入りしてしまったのであった。結局のところ当たり前のようにワタシはたくさんの書類をせっせと読まなければならなくなったのである。いつものように、手を抜くために色々とクダラナイことをして、結局のところ作業量は全然減らなかったのである。昔の小さな銀行泥棒の根性は全然直っていなかったのである。のび太とドラえもんの一人二役マッチポンプ人生はまだまだ終えられそうにないのが、ちょっと哀しい今日この頃、なのである。
2004-10-21[n年前へ]
■平均余命の簡易推定式
平均余命の簡易推定式を見る. 自分の余命の短さに驚き、「この簡易推定式の推定誤差は65才から90才の範囲で 0.45 才以下である」という言葉にさらに驚く。ふと気づくと、これは高齢者向けということなので、平均余命の簡易推定式を見る。それにしても、日本の女性は長生きするなぁ。
2005-01-08[n年前へ]
■「整数と小数」と「言葉と感情や雰囲気」
「元々はそんなに意味がなかった」という、"point"と"residual"という名前を見て、一番最初に思い浮かべたのは「円周率は約3でいいか(2000/9/28 AM 11:05辺り)」でした。円周率πと(πの小数点"point"以下を切り捨てた、あるいは、円周率πを一番近い整数に整えた"adjust")3の間には、無限に続く少数で表される残差"residual"があるわけですが、この「円周率や誤差」辺りの話を読んで感じたこと(それをなかなか言葉で言い表せなかったりするのですが…)を思い出しました。
点"point"で指し示しされたものと本来の何かとの残差"residual"や、小数点"point"で切り捨てられがちな残り"residual"の何か、あるいは、「厳密な意味からもれてしまいがちなある種の感情や雰囲気」といったものを思い出したわけです。
むしろいとうせいこう氏のような(数式を言葉とみなせない)文科系作家は、言葉の厳密な意味からもれてしまいがちなある種の感情や雰囲気といったものを表現していくのが主たる仕事ではないんだろうか。
お笑いパソコン日誌 「円周率は約3でいいか」
2005-02-11[n年前へ]
■「四捨五入と五捨五入」
おれカネゴン「算数記」経由で「日記における四捨五入」を読んでみる。「自分の中の何かを四捨五入して、切り捨ててみたり・切り上げてみたり、そういう感覚はあるかもね」なんて考えながら、ふと、心に思い浮かぶのは四捨五入ではなくて、五捨五入(JIS Z 8401 特にiii項)(ISO31-0)。
自分の中の何かだったり、自分自身が、四捨五入される感覚というのはありがちなものだと思う。今時の季節であれば、もしかしたら受験生なんかはそんな感覚を持つことも多いかもしれない。四と五ではほんの一つしか違わないのに、四捨五入後には大違いになるのだから、自分の力が四以下にならないように、なんとか五以上までがんばって上げないと…なんて思ったりしたことがある人も多いかもしれない。捨てられるか捨てられないかの瀬戸際で、自分自身の桁の数値を大きくしてみようか、なんて思ったことがある人もいるかもしれない。
四捨五入では、「どこかの桁」が切り捨てられるか切り上げられるかは、その桁自身の値の大小で決まる。ところが、五捨五入だと(もちろん、この方法を使う必然性があるわけだけれども)その桁を切り捨てるか・切り上げるかは、(その桁ではなくて)その上の桁が偶数か奇数かで決めてしまう。つまりは、自分が切り捨てられるか切り上げられるかの運命決定権は自分の上の桁が持っていて、その桁がサイコロを適当に振って自分の行く末を決めてしまう。「自分を四捨五入する」と「自分が五捨五入される」のと、どちらがありがちなのかはわからないけれど、どちらもよくありそうな話だ。
「日記における四捨五入」の話に戻るなら、「四捨五入は必ずプラス側に誤差を生じる」という言葉を、この場合にはポジティブに眺めてみるのも、それはそれで良いのかもしれない。今回のような話題であれば、そういったこともあるかもしれないから。「四捨五入で必ずプラス側にシフトする」といったようなことが、少しはあるかもしれないから。
(ところで、こんな話題を書こうとする時、いつも「おれカネゴン文体」霊に憑依されそうになるのは一体何故なのだろう【人は誰しもおれカネゴン】)
」など。
