1999-02-28[n年前へ]
■分数階微分の謎 
線形代数、分数階微分、シュレディンガー方程式の三題話
分数階微分?
InterLabの1999No.5を読んでいると面白い記事があった。いわき明星大学理工学部の榊原教授の「Waveletと数式処理ツール」という記事である。といっても、興味を持ったのはWaveletのことではない。もちろん、Waveletに興味がないわけではない。この榊原教授が講師を務めたWavelet講習にも参加したこともある。しかし、今回興味を惹かれたのはその記事中にあった「分数階微分の解析」である。InterLabの榊原教授の記事を引用すると、-通常微分・積分は整数回実行できるが、分数階微分はこれを分数に一般化したものである。さまざまな物理や工学の現象の記述に使われるようになった-とある。一階微分とか二階微分というものはよく使うが、0.5階微分などというものは使ったことがない。どのようなモノなのかさえよくわからない。
参考:
一体、どんな物理や工学の現象の記述に使われているのか知りたくなったので、infoseekで調べてみる。すると、いわき明星大学の清水・榊原研究室の「粘弾性動モデル」が引っ掛かる。
参考:
衝撃吸収・シリコーンの弾性率などに興味を持っている人には面白いかもしれない。もう少し調べてみると「バナッハ空間バナッハスケールにおける分数階積分作用素」というようなキーワードも引っ掛かる。
そこで、まずは勝手に分数階微分について考えてみた。
分数階微分・積分の勝手な想像図
まずは、イメージを考えるためにグラフを作成してみる。x^2の関数、および、それを微分・積分した関数である。微分は3階まで、積分は2階まで行っている。
 |
このグラフ形式の表示をちょっとだけ変えてみる。
 |
ここまでくると、平面グラフにしてみたくなる。つまり、微分・積分の階数を離散的な整数値でなく、連続的な値としてのイメージに変えたくなる。
 |
これで、微分・積分が整数階でない場合のイメージ(勝手な)ができた。微分・積分が離散的なものではなくスムーズにつながっているものであるというイメージである。図.2から図.3への変化をよく覚えていてほしい。
といっても、これは数学的なイメージのみで物理的なイメージはまだここでは持っていない。位置、速度、加速度などの微分・積分で選られるものに対して同じようなイメージを適用すると、位置なんだけれどちょっと加速度っぽいもの、とか、速度と加速度の「合いの子」みたいなものというような感じだろうか?
さらに、これから先は、f(x)という関数が示す無限個の値を位置ベクトルと考えて、f(x)というのは無限次元空間の一つの点だというイメージを持つことにする。線形代数を考えるならそれが一番わかりやすいだろう。任意の階で微分された関数群が集まって、さらに高次元の空間をなしているというイメージである。
分数階微分を調べる
勝手なイメージはここまでにして、手元にある数学の参考書の中から手がかりを探してみた。すると、大学院入試問題解説 - 理学・工学への数学の応用 - 梶原壌二 現代数学社ISBN4-7687-0190-6
の中に手がかりがあった。あれ、ということは以前にやったはずなのか...そう言えばおぼろげな記憶がちょっと...
その中の言葉を少し引くと、
フーリエ変換は等距離作用素である、関数空間L^2(R)における回転といえる。結局、
となる。そして、古典力学におけるハミルトン関数において、運動量を微分演算子で置き換えれば、量子力学や量子化学のハミルトン演算子が得られ、シュレディンガー方程式などにつながるのである、とある。他の資料を眺めてみると、どうやら量子力学などの分野からの要請に応じてここらへんの微分演算子の分野が発展しているようだ。理論物理などをやった方ならよくご存知のことだろう。例えば、水素原子の基底状態の波動関数へ運動エネルギーの演算子を作用させるというような、基本的な所でも、このフーリエ変換を用いた微分演算が用いられてる。ここで、fは元の関数であり、Fはフーリエ変換
さて、この式自体は非常に簡単である。それにイメージも湧きやすい。
i を掛ける演算、私のイメージでは複素数空間の中で90度回転をする(言い換えれば、位相が90度ずれる)演算、が微分・積分であるというイメージはスムーズに受け入れやすい(それが正しいかどうかは知らないが)。なぜなら、微分が空間の中での回転であるとすると、三角関数の微分・積分に関する性質(例えば、Sinを微分するとCosに、Sinを2階微分すると-Sinになる、すなわち、一回の微分につき位相が90°ずつ回転する(位相がずれる)というような性質)が納得でき、それがフーリエ変換という形で登場してくることがスムーズに受け入れられるのである。また、微分といえばとりあえず三角関数の登場というイメージもある。
もう少しわかりやすく書くと、
- 三角関数では一階微分の結果は90度位相がずれる(回転する)。
- ならば、(例えば)0.5階微分は45度位相をずらせば良い。
- 任意の関数もフーリエ変換により、三角関数に分解される。
- ならば、任意の関数に任意の実数値の微分が成立する。
任意の関数をフーリエ変換し三角関数に分解した時の位相、言い換えれば、周波数領域での位相ずらし、で分数階微分が定義されるということは、物理的実用的に大きな意味を持つ。例えば、電磁波、弾塑性運動などの物理現象の中での位相変化を分数階微分で解けることになる。例えば、複素貯蔵弾性率などについて分数階微分との関係は深そうである。あるいは、媒体中の電磁波の位相などについて適用するのも面白そうである。
分数階微分を使ってみる
よく分からないところも多いが、とりあえず、
という式を使ってみる。まずは、使ってみないとわからない。とりあえず、1次元の関数を作成して、この式を適用してみる。まずは、よく出てくるガウス分布で適用してみる。まずはガウス分布とそれの通常の一階微分の解析解を求める。
 |  |
それでは、今回の方法による一階微分の結果と、それと解析解との比較を示す。なお、本来無限領域のフーリエ変換を有限の領域で行っているため、端部近くで変なことが生じるのはしかたがないだろう。また、色々な事情により係数の違いは無視して欲しい。
 |  |
ちょっとずれが生じているが、こんなものだろう。しかし、これだけでは今回のフーリエ変換を用いた微分の面白さはでてこないので、0から2の範囲で連続的に分数階微分をしてみる。
 1/10 (=0.1)階微分 |  1/2 (=0.5)階微分 |  7/10 (=0.7)階微分 |  1階微分 |
 13/10 (=1.3)階微分 |  15/10 (=1.5)階微分 |  17/10 (=1.7)階微分 |  2階微分 |
モーフィングのようで面白い。
さて、今回は分数階微分を勉強してみる所までで、これの応用は別に行ってみたい。もちろん、言うまでもないと思うが、間違いは多々あると思う。いや、田舎に住んでいるもので資料がないんですよ。
1999-06-10[n年前へ]
■コピー機と微分演算子 
電子写真プロセスを分数階微分で解いてみよう
前回、
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
の中で、電子写真プロセスは「画像のエッジ部分が黒くなり、そうでないソリッド部分は画像が飛びやすい... 画像のエッジ部分、すなわち、電位変化が大きく、電界強度の高い部分に対してトナーが現像されやすい... 」という文章がある。この脈絡は何か見覚えがないだろうか?そう、
分数階微分に基づく画像特性を考えてみたい-同じ年齢でも大違い-(1999.02.28)
の中の、「人間が画像を感じる特性というものは、画像強度と画像強度変化(画像強度の一階微分)の中間的なものであると言うことができるかもしれない。」という文脈と似ている。また、「ゼロックス...」の回での(昔の)電子写真の特徴、
- エッジ強調される。
- 細かいところはボケてしまう。
参考までに、以前の話のときに用いた画像を示しておく。
まずは、
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
における(昔の)モノクロコピーを模したものである。
 |  |
分数階微分に基づく画像特性を考えてみたい-同じ年齢でも大違い-(1999.02.28)
の際に解析した元画像と0.75階画像である。ただし、この解析は2次元解析ではなく、1次元における計算を回転させて、中心対称な画像を作成している。その理由は前回述べたので今回は述べない。
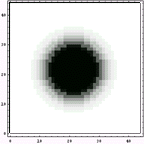 | 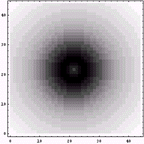 |
それでは、解析を始める。まずは、Photoshop5による「(昔の)コピー機シミュレーション」である
 |  |
次が、分数階微分画像だ。今回もMathematicaを用いて計算している。検算が終了したら、Notebookも公開予定だ(実は検算が終了していないのだ...)。
 |  |
胸を張って「似ている」と断言するつもりはないが、少しは似ているのではないだろうか。別に似るまでがんばっても良いのだが、この分野の話はあまりやりすぎるわけにはいかないのである。ということで、強引ではあるが、今回の話の結論は「アナログコピーはオリジナルコピーの0.75階微分だ」というところで終わらせてもらう。
今回は、コピー機によるコピーを微分演算子と結びつけてみたわけだが、複数回のコピーに適用してみると面白いだろう。例えば、孫コピーは0.75+0.75階微分=1.5階微分であるとかだ。
また、同じ現像プロセスといっても色々あるわけであるから、各現像方式により微分演算子の階は異なるのが適当だろう。例えば、この機械は0.8階微分(つまりほとんどエッジ現像)であるが、こちらの機種は0.05階微分(極めて元画像に近い)で再現性に優れる、などという論議もできるかもしれない。
ところで、某所で今回の話と似て非なる話がCoffeeBreakとして公開されている。しかし、そちらは一般公開されていない。というわけで、今回は分数階微分の第3話ではなく、第4話ということになる。STARWARS風に言えば、Episode4だ。STAR WARSのようなSF映画もそうであるが、こういった話は生物(なまもの)である。ずっと置いておくと腐ってしまう。「腐ってこそ美味い食べ物もある」、という反論も聞こえてきそうだが、そういったものは少数の例外である。味オンチの料理人の作ったものではあるが、どうか賞味期間内に味わって頂きたい。
1999-07-18[n年前へ]
■hixの地図 
好きな話は何処にある?
最近、本WEBのTopページが非常に読みにくくなっている。話題が多すぎるのだ。これでは、このWEBを見に来てくれた人がいたとしても、迷ってしまうだろう。きっと、好みに合うページを見つける前に他のWEBサイトにとんでしまうに違いない。自分の好きにやっているサイトとは言え、それは少し寂しい。そこで、自らhiraxサイトの内容について解説してみることにした。といっても、単に解説するのではつまらないので、多少の考察を含めながら、である。
他の人のWEBなどを眺めながら、自分のWEBの特徴を振り返ってみると、下のような図を持ち出すのが一番良いような気がする。これは横軸を「技術度」、縦軸を「感性度(完成度にあらず)」にしたものである。ジャンル1,2,3,4は大雑把に傾向で分類しようとしたものである。
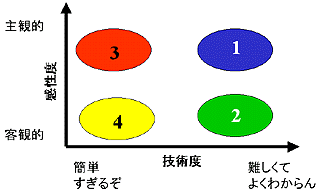 |
他の技術系サイトを見た後に本WEBを見ると、どうも本WEBは技術的でない話が多い。主観的な部分がかなり含まれているのだ。他の技術サイトでももちろん主観的な部分はある。しかも、(私にはまだまだ出来ないのだが)説得力があるのだ。すなわち、ある程度の客観性が感じられる。しかし、私のサイトの中にある主観的な話は他の人に説得力があるとは思えないのである。妙な感覚的な話と技術的な話のカクテルみたいなのである。そこで、上のようなグラフが登場するわけである。
科学という立場から考えれば、客観的であり技術的にも高度な「ジャンル-2」が望ましいだろう。しかし、本WEBには技術的には高度でないし、客観性もない、という「ジャンル-3」も多い。例えば、
iMacはドラえもんの夢を見るか? -さようなら、ドラえもん - (1999.02.03)
などがそうだ。そして、その極限として「Scraps」がある。こういった状況が良いのか悪いのかよくわからないが、とりあず、それもまた個性ということにしておこう。
「ジャンル-4」の代表的な話としては
鴨川カップルの謎 -そうだ、京都、行こう-(1998.11.29)
というところか。「ジャンル-1」としては
コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
というところで、「ジャンル-2」は
夏目漱石は温泉がお好き? -文章構造を可視化するソフトをつくる - (1999.07.14)
という感じだろう。まずは、自分の好みとあった所から眺めてみて頂きたい。また、裏で繋がっている話も多いのでそういう伏線を探してみるのも面白いのではないだろうか。
なお、私の書く文章ははどうも「本当に言いたいことを行間に隠してしまう」ようなので(表現力がないとも言う)、行間に隠れている(作者も気づいていない)応用など読みとって頂けたら幸いである。それを私に教えていただければ、なお良い。
1999-09-01[n年前へ]
■画像に関する場の理論 
ポイントは画像形成の物理性だ!?
今回は、
夏目漱石は温泉がお好き? - 文章構造を可視化するソフトをつくる- (1999.07.14)
の回と同じく、「可視化情報シンポジウム'99」から話は始まる。まずは、「可視化情報シンポジウム'99」の中の
ウェーブレット変換法と微積分方程式によるカラー画像の圧縮および再現性について
という予稿の冒頭部分を抜き出してみる。「コンピュータグラフィックスを構成する画素データをスカラーポテンシャルあるいはベクトルポテンシャルの1成分とみなし、ベクトルの概念を導入することで古典物理学の集大成である場の理論が適用可能であることを提案している」というフレーズがある。
着目点は面白いし、この文章自体もファンタジーで私のツボに近い。しかしながら、肝心の内容が私の趣向とは少し違った。何しろ「以上により本研究では、古典物理学の場の理論で用いられるラプラシアン演算を用いることで、画像のエッジ抽出が行えることがわかった。」というようなフレーズが出てくるのである。うーん。
私と同様の印象を受けた人も他にいたようで(当然いると思うが)、「エッジ強調・抽出のために画像のラプラシアンをとるのはごく普通に行われていることだと思うのですが、何か新しい事項などあるのでしょうか?」という質問をしていた人もいた。
また、話の後半では、画像圧縮のために、ラプラシアンをかけたデータに積分方程式や有限要素法などを用いて解くことにより、画像圧縮復元をしようと試みていたが、これも精度、圧縮率、計算コストを考えるといま一つであると思う(私としては)。
画像とポテンシャルを結びつけて考えることは多い。例えば、「できるかな?」の中からでも抜き出してみると、
- 分数階微分に基づく画像特性を考えてみたい- 同じ年齢でも大違い - (1999.02.28)
- ゼロックス写真とセンチメンタルな写真 - コピー機による画像表現について考える- (99.06.06)
- コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
現実問題として、実世界において画像形成をを行うには物理学的な現象を介して行う以外にはありえない。「いや、そんなことはない。心理学的に、誰かがオレの脳みそに画像を飛ばしてくる。」というブラックなことを仰る方もいるだろうが、それはちょっと別にしておきたい。
「できるかな?」に登場している画像を形成装置には、
コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
で扱ったコピー機などの電子写真装置や、
宇宙人はどこにいる? - 画像復元を勉強してみたいその1-(1999.01.10)
で扱ったカメラ。望遠鏡などの光学系や、
ヒトは電磁波の振動方向を見ることができるか?- はい。ハイディンガーのブラシをご覧下さい - (1999.02.26)
で扱った液晶ディスプレイなどがある。そのいずれもが、純物理学的な現象を用いた画像形成の装置である。
例えば、プラズマディスプレイなどはプラズマアドレス部分に放電を生じさせて、電荷を液晶背面に付着させて、その電荷により発生する電界によって液晶の配向方向を変化させて、透過率を変化させることにより、画像を形成するのである。
 |
また、逆問題のようであるが電界・電荷分布測定などを目的として液晶のボッケルス効果を用いることも多い。液晶を用いて得られる画像から、電界分布や電荷分布を計測するわけである。これなども画像と場の理論が直に結びついている一例である。
参考に、SHARPのプラズマアドレスディスプレイを示しておく。
 |
また、電子写真装置などは感光体表面に電荷分布を形成し、その電位像をトナーという電荷粒子で可視化するのであるから、電磁場を用いて画像形成をしているわけである。だから、場の理論を持ちこむのは至極当然であり、有用性も非常に高いだろう。そういった視点で考察してみたのが、
である。 同様に、画像圧縮に関しても、画像形成の物理性に着目することで実現できる場合も多いと思うのであるが、それは次回にしておく。
2000-04-09[n年前へ]
■心に浮かぶハートマーク 
色覚の時空間特性で遊んでみよう
4月である。「四月物語」の4月である。
で書いたように、私は4月だけは英語の勉強をしたくなるのである(何故なら、全然できないから)。そこで、ここのところ英語の先生のところに足繁く出向いている。その時に、信号機の例題を出されて「青信号」と言おうとして私は"ablue light"と言ってしまった。すると、「青信号は"green"だ -> The run signalis green.」と言われてしまった。しまった、確かにその通りだ。いや、英語でそう表現することに納得という話ではない。英語ではこうだと言われたら、私はそのまま頷くのみである。"Yes,sir"状態である。納得したのは、信号機の「現実の」色の話だ。そう言えば、日本でも信号機は「緑色」だった。試しに、信号機の一例を次に示してみる。 実は人にそう優しくないユーザーインターフェースの一例 |
本当は「緑色」なのに、「何故、青信号と言われていたのだっけ?」と考えながら、帰り道に交差点、「緑」信号をじっと見ていた。すると、「緑」信号は消えて、黄信号になった。しかし、私の目にはその瞬間「赤」信号が見えたのである。
私は夢を見ていたわけでも、予知能力があるわけでもむろんなくて、それは単なる錯覚である。「緑」信号が消えた瞬間に「赤」信号が見える、という錯覚である。
私が見た「赤」信号機の錯覚を実感してもらうために、こんなアニメーションGIFを作ってみた。ソフトをレジストしてないが故の、SGという文字は気にしないでもらいたい。下の画像中央にある黒い点を見つめていて欲しい。すると、緑のハートマークが消えた瞬間から、赤いハートマークがおぼろげに見えるはずである。
|
これは、色覚の時間特性による錯覚の一つである。実際に、赤いハートマークがあるわけではない。私の心の中にだけ、浮かぶハートマークである。
その原因となる色覚の時間特性を示すグラフを以下に挙げる。これは色覚の時間特性を示すグラフの例である。色覚のインパルス応答のようなものである。ある色を見た後には、その色の反対色を感じるということを示している。
 |
このような錯覚というのはとて興味深いものである。視覚という「デバイスの特性」が「目に見えて実感できる」ことが特に面白い。以前、
- 分数階微分に基づく画像特性を考えてみたい-同じ年齢でも大違い-(1999.02.28)
- コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
- ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
さて、先の錯覚は色覚の時間特性によるものだった。それと全く同じような錯覚が、色覚の空間特性から得ることができる。そのような錯覚の一つにこのようなものである。それを下に示してみる。
 |
この有名な画像パターンを見れば、「白い線の交差部が赤く見える」はずだ。
これは、色覚の空間特性によるものである。これを示すグラフの例を以下に示す。この場合もやはり色覚の時間特性のように、ある刺激があるとその周囲に反対の色の影響が表れる。例えば、周りに白が多いと、その部分は黒っぽく見える。赤色の周りは緑がかって見えるのである。逆に緑色のものの周りは赤く見えるのだ。
そして、それをさらに進めると、周囲に赤色が少ない場所は、周りに比べて赤く見えるのである。上の画像で言えば、白の交差部は、赤の刺激が少ないので、赤の刺激を逆に感じるのである(ちょっと説明をはしょりすぎかな)。
 |
今回は、このような色覚の空間特性をシミュレートしてみたい。道具は単純にPhotoshopだ。もう手作業でやってみるのだ。ネコの色覚で遊んだ
の時と同じである。 | これがオリジナル画像。黒背景に白い線で格子模様が描かれている。 |
 | 白い(つまり光刺激が多い領域)からの影響を考える。先に示したグラフのように、光刺激がある箇所と少し離れたところではそれと逆の刺激を受けたような効果がある。 そこで、まずは白い部分からの影響をガウス形状のボカシにより、真似してみる。ある画素から少し離れた所に影響が及ぶのをシミュレートするのである。 |
 | 白い部分からの影響(実際には、比較問題となるので黒い部分からの影響と言っても良いだろうか?)は「白と逆の方向、すなわち黒い方向」に働く。 そこで、上の画像を階調反転させる。すなわち、ある画素から少し離れた所に元の明るさと逆の影響が及ぶことをシミュレートするのである。そしてさらに、階調のカーブを鋭くしてやる。 |
 | 上で計算したものとオリジナルの画像を加算してやる。これが、人間が感じる画像をシミュレートしたものである。 白い格子の交差点部が黒く見えているのがわかると思う。といっても、もともとその部分は黒く見えていたとは思うが。 下に、シミュレート画像とオリジナル画像を並べてみる。 |
 |  |
このようにして、オリジナル画像を見たときに感じる錯覚をシミュレートできたことになる(もどきだけど)。
さて、上では簡単のためにグレイスケールで遊んでみたが、最初に示した赤白の場合のようなカラーの例を示してみる。次に示す四角形の中央部は、右と左ではいずれも右の方が赤っぽく見えるはずである。緑に囲まれた領域は、本来の色に対して、緑と逆の赤色に見えるのである。上に示した白黒格子と全く同じ理屈である。
|
|
|
|
さて、この右下の画像中の赤は通常の「赤」よりもさらに鮮やかな「赤」を実現していることになる。左下のものと同じ赤100%の色であるが、左よりももっと鮮やかに見えている筈だ。右下と比べると、左下の赤は落ち着いた赤色に見えてしまうのではないだろうか?
この右下の赤、すなわち緑に囲まれた赤は、物理的にCRTあるいは液晶(今あなたがこのWEBページを見ているデバイス)などの表現可能領域を越えた、さらに鮮やかな赤色に見えているわけだ。ヒトの視覚のデバイス特性が故に鮮やかに見えることになる。
さて、鮮やかな「赤」と言えば、「ポケモンチェック」によれば、日本民間放送連盟のガイドラインには
- 映像や光の点滅は、原則として1秒間に3回を超える使用を避けるとともに、次の点に留意する。
- 「鮮やかな赤色」の点滅は慎重に扱う。
- 前項1の条件を満たした上で1秒間に3回を超える点滅が必要なときには、5回を限度とし、かつ、画面の輝度変化を20パーセント以下に押さえる。加えて、2秒を超える使用は行わない。
- コントラストの強い画面の反転や、画面の輝度変化が20パーセントを超える急激な場面転換は、原則として1秒間に3回を超えて使用しない。
- 規則的なパターン模様(縞模様、渦巻き模様、同心円模様など)が、画面の大部分を占めることも避ける。
しかし、その「赤」と「緑」パターンが細かくなると、何故だか不快なのだ。色覚の時空間特性を考えると、「赤」と「緑」の細かいパターンというのは、もしかしたら読む際に刺激が強すぎるのではないか、と想像してみたりする。根拠はたいしてないのだけれど。




