hirax.net::Keywords::「回転」のブログ

■Evey little thing we ee is magic.　

WEBページで作るOscylinderscope

　先日、The Reuben H. FleetScience Centerという科学館に遊びに行った。そこで面白いものをみかけた。それはOscylinderScopeという名前のもので、下の写真のようなものだった。
 

Oscylinderscope

リンク先はhttp://www.normantuck.com/catalogPages/oscylinderScope.html

　Oscylinderscopeの作者のNorman TuckのWEBサイト

• A Catalog of Kinetic Sculpture byNorman Tuck
• ( http://www.normantuck.com/ )

• TheOscylinderScope
• ( http://www.normantuck.com/catalogPages/oscylinderScope.html)

　電気的な変化する信号に合わせて、光の点をsweepさせることで波形を描き出すのがオシロスコープだが、このOscylinderScopeもドラムをい回転させて、ドラム上に描かれた白い線が振動するギターの弦の後ろをsweepして、ギターの弦の振動する様子を描き出すのである。

　参考までにNorman TuckがOscylinderScopeに関して取得しているUnites StatesPatent 5,975,911から判りやすそうな図を下に示しておく。揺れる棒の様子がSin波状に見えている、という説明図である。
 

United States Patent 5,975,911

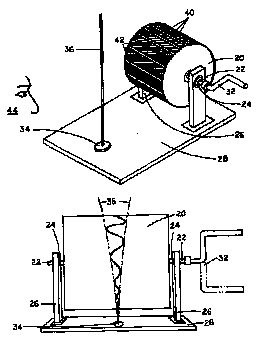　このOscylinderScopeにはとっても単純だけど素敵な科学的なアイデアと、展示物としてのセンスと、そして何故かちょっとうれしくなるようなバカバカしさが感じられて私はとっても大好きだ。そこで、一ファンとして私も「WEBページで作るOscylinderscope」というのをやってみることにした。

　といっても、やることは単純に単なる速く移動する白い線をパソコン画面に映し出すだけである。そして、その前で何かを振動させてその振動の様子を可視化するのである。

　まずは、Oscylinderscope風アニメーションGIFだ。おそらくInternetExplorerではゆっくりとしか再生されないと思うが、NetscapeCommunicatorであればプラットホームにもよるが高速に再生することができると思う。少なくとも、Linux上のNetscapeNavigatorではかなり速く再生されるハズだ。
 

Oscylinderscope風アニメーションGIF

　このアニメーションを再生できない環境の人のために、動画ファイル版にしたものもここにおいておく。

• oscylinderscope.avi ( 145kB )

　このアニメーションGIFや動画ファイルを再生して、部屋の電気を暗くしてみる。すると、CRTの画面というのはとても明るいので、部屋を暗くしてCRTだけをつけておくと、CRT画面に映し出されている色に部屋が染まる。部屋がそんな風にチカチカした状態で、画面の前で何かを振動させると、アラ不思議その物体の振動の様子が何やら変な風に見えてくる。例えば、真っ直ぐな細い棒を「Oscylinderscope風AVIファイルの前で棒を揺らしてみたところ」である。写真では判りにくいと思うが、真っ直ぐな棒がウニョロウニョロと曲がって見えるだろう。とにかく、真っ直ぐな棒が振動する様子を静止したイメージで目にすることができるのだ。
 

Oscylinderscope風AVIファイルの前で棒を揺らしてみたところ

　ところで、私はこんなOscylinderscopeを見ていると、ナポレオンズの「首グルグル・マジック」を連想してしまう。一カ所だけ穴の開いた筒を頭にかぶる。そして、穴の部分から顔を覗かせる。筒を回転させ始めると、なんと顔がずっと見え続ける、つまりエクソシストの少女のように首が回転しているのだ！これがマジックかぁ？と言う人も多いかもしれないが、私はこれこそ本当にmagicそのものだと思う。このマジックには、目に見えていない瞬間に起きていることは結局想像するしかない、という本当の真実と、何故かもう嬉しくなるくらいのバカバカししさが同居していて私は大好きなのだ。他の人はどう思うか知らないけれど。
 

■ブランコの中の∞(無限大)　

なんで一体漕げるのだろう？

　もちろん、そこは子供の領分というだけではなくて、黒沢明の「生きる」の主人公がしていたように「大人がブランコに座って揺れていたり」すると、思わずその人の陰に隠れている物語を想像したりしてしまう。ブランコの周りというのはそんな不思議な雰囲気を持っているのだ。

　やたらにブランコを漕ぐのが上手いガキんちょもいる一方で、全然ブランコを漕げず四苦八苦する子供もいる。ブランコを漕ぐコツを覚えるのもなかなか大変そうである。考えてみれば、ブランコは一体どういう風に漕ぐものなのだろう？口で上手く説明できる人がいるだろうか？

　それに、そもそも私たちはブランコを何故漕ぐことができているのだろう？

　いったい、いつから疑問に思うことをやめてしまったのでしょうか?　いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか?
　いつだって、どこでだって、謎はすぐ近くにあったのです。
　何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。

　もちろん、「何でブランコの漕ぎ方が不思議なのさ？」と言う人も多いだろう。その中には理路整然とブランコの漕ぎ方を説明してくれる人もいるだろう。そして、「特にブランコの漕ぎ方をじっくり考えたことなんかないもんね」という人も多いに違いない(私だけかもしれないが)。そこで、まずは「ブランコの不思議」を簡単に書いてみることにしよう。

　次の図は「ブランコを漕いでる子供」である。
 

ブランコを漕いでる子供

　この子供が何もせず立っているだけ(あるいは座っているだけ)だったら、どうなるだろうか？それはもちろん、単なる振り子と同じくようにブランコは動く。もしも色々な摩擦がなければ、まったく同じように動き続けるだけだし、摩擦力があればブランコの動きはただ減衰していくだけである。つまり、子供が何もしなければ、ブランコの動きは「遅く・小さく」なることはあっても、ブランコが「速く・大きく」なることはないのである。

　だからブランコを速くするためには、「ブランコに乗ってる子供がブランコを漕がなければならない」わけであるが、ブランコに乗ってる子供は一体どんなことができるだろうか？

　次に示す図は「ブランコに乗ってる子供を中心にとった座標軸」を描いてみたものだ。この図の中で直交する二つの軸を描いてある。つまり、

1. ブランコの動きの中心を向いている軸A
2. 軸Aに直交する、つまりブランコの進行方向(あるいはその逆方向)を向いている軸B

ブランコに乗ってる子供を中心にとった座標軸

　ところが、実は「ブランコに乗ってる子供」はこの二つの軸の内の片方、軸Aに対しての動きしかできない。何故なら、軸B方向に対しては「ブランコに乗ってる子供」動きの支えになるモノが全然無い。だから、ツルツル滑る氷の上では全然動けないのと同じく、「ブランコに乗ってる子供」はその方向には動けないのである。もし子供がその方向に動こうとして体を動かしたりしても、結局子供の重心はその方向には全然動かないのだ。

　それに対して、ブランコの動きの中心を向いている軸A方向に対してはブランコの鎖も座っている(あるいは立っている)板が支えになるわけで、その方向に対しては「ブランコに乗ってる子供」は動くことができる。

　というわけで、ブランコの上では「ブランコの動きの中心を向いている軸A」方向にしか動けないわけであるが、その方向というのはブランコの進行方向に対しては直交している。つまり、ブランコを漕ぐためには、「ブランコの進行方向に対して直交している方向に動く」しかないことになる。

　ここまで書くと、ブランコの不思議が判るハズだ。ブランコを漕ぐ、つまりブランコを軸B方向の速度を上げたいのに、我々は「軸Bに対して直交している方向に動く」ことしかできないのである。一体何故、軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増すのだろうか？　この謎「ブランコの不思議」を、ゆっくり考えてみることにしよう。
 

　まずは、ブランコに乗ってる子供が立ち上がったりして、「ブランコの動きの中心を向いている軸A」方向に動いた場合、何が起きるだろうか？
 

ブランコに乗ってる子供が立ち上がったりすると、何が起きる？

　「ブランコの動きの中心を向いている軸A」方向に動くと、ブランコの鎖の長さが短くなることと同じである。すると、回転しているブランコの鎖が短くなるわけで、そうするとブランコの速度は速くなる。何故なら、角運動量が保存されるからである。ちょうど、スケートのフィギア競技の選手が回転中に伸ばしていた手を縮めると回転数が早くなるのと同じだ。

　もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの半分だけ(とんでもない身長の子供だ！)上がれば、ブランコの速度はもとの速度の倍になるのである！

　ということは、少なくともこの瞬間は「軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増す」わけであるが、これでブランコの漕ぎ方を納得するにはまだまだ早いのである。確かに、「ブランコの動きの中心を向いている軸A方向に動く」とブランコの速度は増すわけであるが、それはその瞬間だけである。ブランコの上で「立ち上がり続ける」なんてことはできないわけで、速度が増し続けるわけではないのである。

　もしも、「もう一度ブランコの上で立ち上がるために、すぐに低い姿勢に一旦戻ったり」したら大変だ。ブランコの鎖の長さが長くなるのだから、今度はブランコの速度は遅くなってしまうのである。

　もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの二倍だけ(つまりさっき立ち上がった逆の動きである)下がれば、ブランコの速度はもとの速度の1/2になってしまうのだ！
これでは、結局さっきの速度が二倍になったことは帳消しになってしまう。つまり、「単純に」角運動量の保存を考えるだけではブランコの速度を(長い間にわたって)早くしていくことはできないわけだ。

　このままでは、「ブランコを漕ぐことなんか不可能である」という結論が出てしまいそうになるが、ブランコを漕いでる子供達はイッパイいるわけで、そんな結論を受け入れるわけにはいかない。彼らがみんな超能力でブランコを漕いでいるわけもないのである。まだまだ見落としていることがあるので、ブランコの不思議の謎が解けないだけのハズなのだ。
 

　そこで、ちょっと考えてみると「とんでもなく単純なこと」を見落としていたことに気付いた。それは、「タイミング」である。例えば、ブランコの速度がずっと同じであるすると、

1. 初期のブランコの速度 = 10
2. 重心位置を高くして 10 X 2 = 20　(やったぁ、速度が二倍だぁ！)
3. 重心位置を低くして 10 Ｘ 1/2 = 10　(何てこったい、速度が半分になっちまったか！)

1. 初期のブランコの速度 = 10
2. 重心位置を高くして 0 X 2 = 20　(やったぁ、速度が二倍だぁ！)
3. そのあとブランコの速度 = 0
4. 重心位置を低くして 0 Ｘ 1/2 = 0　(0が0になっても全然変わってないもんね！ヘヘン！)

　人生何事もタイミングが重要である。失恋した男性や女性にタイミングをわきまえた「恋のハイエナ」達が寄ってくるのと同じく、またお金に困っていると何故かサラ金の広告が目の前にチラチラするのと同じく、ブランコを漕ぐにはやはりタイミングが重要なのだ。
 

　なるほど、考えがまとまってきた。このイキオイでそのまま「ブランコの理想の漕ぎ方」まで考えてしまおう。

　まず、「重心位置を高くしてブランコの速度早くする」にはできるだけ速度が速い瞬間に行うのが良いだろう。倍率が確定している賭なのだから、元金はあればあるほどおトクである。１万円×２=二万円では１万円しかもうからないが、一千万円×２=二千万円では一千万ももうかるのだ。ブランコの速度が速い瞬間に立ち上がれば、一番おトクに速度を増すことができるのである。

　もちろん、ブランコの速度が速い瞬間といえば、明らかにブランコが一番下にきた瞬間である。つまり、ブランコが一番下にきた瞬間に立ち上がれば「一番おトクに速度を増すことができる」わけだ。しかも、その瞬間は鉛直に重心を持ち上げることになる。つまり、位置エネルギーを効果的に増加させることができるわけだ。結局、この時に増加させた位置エネルギーは後で、運動エネルギーに変換されるわけで、結局これがブランコの運動の源となるのである。

　そして、「次にもう一度立ち上がるために一旦低い姿勢に戻る瞬間」=「速度が遅くなる瞬間」はブランコが停止しているときであれば何の問題もない。ブランコはもともと止まっているんだから、その速度が何分の一になったって全然気にしないもんね！となるわけだ。そのタイミング= ブランコが止まる瞬間といえば、もちろんブランコが最高地点まで上がった瞬間である。つまり、ブランコが一番上にいった瞬間に低い姿勢に戻れば全く減速無しに次の加速に備えることができるわけである。しかも、その時には実は運動エネルギーを位置エネルギーに変えることで、隠し財産にしているわけで、もう汚い政治家のマネーロンダリングのような見事な方法なわけだ。

　というわけで、

• ブランコが下に来たときに(立ってる場合は)足を伸ばして立ち上がったり、(座ってる場合は)足を曲げたりすることにより高い位置に重心を持ってきて(しかも、重力に逆らって重心を上げるため位置エネルギーが増加する)
• ブランコが上に行ったときにその姿勢を元に戻す

　それでは、確認のためにそのやり方で本当にブランコが漕げるのかどうか、シミュレーション計算を行ってみた。ブランコの動きは振り子運動だが、振れ幅がとても大きいので、cosx≒xというような近似をする単振動としての扱いはできない。そこで、楕円積分の計算を行わなければならない。が、私が自分の力でできるかどうかはともかく、そこはMathematicaに解かせればイッパツである。もう、驚くくらい簡単なのである。自分の力で解いていないところが、実に悲しい現実ではあるが、それが現実なのだからしょうがない。

　というわけで、ブランコの動きのシミュレーションをしてみた結果が次のグラフである。「ブランコに乗ってる子供」の漕ぎ方としては、以下の三つ

1. 何もしない場合
2. ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合
3. ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合

ブランコの動きのシミュレーション結果

1. 何もしない場合 →　ブランコの動きはず〜と変わらない

2. ブランコが下にきたあたりで立ち上がり、 ブランコが上にきたあたりで座り込んだ場合 →　ブランコの動きはどんどん大きくなる 「やったぜ、これが理想の漕ぎ方だぁ。」

3. ブランコが下にきたあたりで座り込み、 ブランコが上にきたあたりで立ち上がった場合 →　ブランコの動きはどんどん小さくなる 「なんてこったい、遅くなっちまったぁ。」

　この結果から、ちゃんと1.の「何もしない場合」は「ブランコの動きはず〜と変わらない」し、理想の漕ぎ方であるハズの2.の「ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合」は「ブランコの動きはどんどん大きくなる」し、最悪の漕ぎ方であるハズの3.の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合」には「ブランコの動きは逆にどんどん小さくなってしまう」ことがわかる。というわけで、今回考えた「ブランコの不思議= 漕ぎ方」はシミュレーション計算結果からも確かめることができたわけだ。

　ところで、こういったタイミングを考えながらパラメーターを変えることで動きを大きくしたりすることは「パラメータ励振」と呼ばれる。ブランコの漕ぎ方はその「パラメータ励振」の応用のひとつである。「何故、リンゴは落ちるのかという謎」には重力という基本的な物理現象が隠されていたが、それと同じく、「ブランコの漕ぎ方の謎」にも「パラメータ励振」という物理現象が隠されているのだ。次回以降も、この「パラメータ励振」を手がかりにいくつかの「身近な謎」に迫ってみたい、と思うのである。
 

　さて、公園でブランコを漕ぎまくる子供をもし見かけたならば、ぜひ横から子供の動きを見てやってもらいたい。きっと、その揺れ動くブランコの中にはこんな∞(無限大)の形が見えるハズだ。天まで上ろうとする「ブランコの秘密」はその「ブランコの中の∞(無限大)」に隠されていたのである。子供も含めて人間の可能性は∞(無限大)だと私は思うが、ブランコの揺れる動きから、そんなことを考えてみるのも少し面白いのではないだろうか？　それとも、ちょっと考え過ぎかな。
 

■心地良い波音　

　画面は90度回転しちゃってます。。（リンク）

■パズルのカケラ　

ジグゾーパズル的プラグインを作る

　大きな写真を20ピクセル四方くらいで分割して、それをタイルのように並び替えてくれて、分割したカケラを自分であとで自由に移動できたり、個別に画像調整もできて…、そんなPhotoshopのプラグインが欲しいので探して下さい。　もしなかったら、作ってくれてもいいです。

　それはさておき、今回の依頼も実に判りやすいのだが、もしなかったら作ってくれてもいいです、とは優しい口調でとんでもない依頼だ。いや、実際のところ依頼というよりほとんど命令である。人を（いや違った、ぐるぐるを）ドラえもんか何かと間違えているんじゃないかー、と聞き返したくなったりするのである。

　しかし、これまで「できるかな?」では「たくさんのカケラを並べて、一枚の絵にするモザイク」で遊んでみることが多かったが、そんなこれまでとは逆のアプローチ、「一枚の絵をたくさんのカケラにばらばらにしてみる」という、まるで一枚の絵をジグゾーパズルのピースに分解してしまうような遊びをしてみるのも面白いかも、ともふと思った。そこで、今回はこの依頼に応えてそんなPhotoshopのジグゾーパズル的プラグインを作ってみることにした。名付けて、Midinette(= 女性店員,、針子さん)プラグインである。「糸のこで切り抜いたパズル」はJjigsawpuzzleだけれど、そんなジグゾーパズルを切り張りしたり繋げあわせたりする賢い女性店員・針子さんという気持ちを込めてみた。
 

　さて、普通なら、Photoshopのプラグインと言えば、普通はフィルター・プラグインなのだろうけれど、今回は「分割したカケラを後で動かしたい」という注文がついているので、アクション・プラグイン（通常のアクションではなくて、あくまでもプラグイン）で適当にちょちょいと作ってみることにした。まずは、このプラグインを使った場合のサンプル画像を下に示してみる。
 

Midinetteの処理画面をちょっとだけ加工したもの

オリジナル画像

変換画像

　アクションプラグインはPhotoshop5.0以降に導入されたものであるが、今回のプラグインは6.0以降の機能も使っているので、Photoshop56.0以降が動作環境となる。また、Windows2000でしか動作チェックしていないので、もしかしたらその他の環境では動かない場合があるかもしれない。その場合はその旨知らせてもらえれば、コンパイルし直したものを作る予定だ。で、いつもと同じようにアルファ版のものをここに置いておく。これをPhotoshopのPlug-Insディレクトリに置けば、ファイル→自動作業からMidinetteが使えるようになる。

• Midinette.lzh ( 29kB )

　この手のジグゾーパズル系のプラグインとしては他にAVBros. Puzzle Proなどがあるが、ピースの形状の自然さはともかく、各ピースを(それぞれレイヤーに変換することで)自由に後で動かすことができるという点で今回のこのプラグインは面白いのではないか、と思う。

　ちなみに、下の画面がMidinetteのダイアログである。現時点で設定可能なパラメータの内容は

• Horizontal Division  : 横方向の分割数
• Vertical Division    : 縦方向の分割数
• Inclination          :長方形からの変形量 (3〜5)
• JigsawPuzzle         : 丸い突起部の大きさ(6〜7)
• Scattering          : ピースをバラバラにするかどうか
• LayerEffects         : ピースの立体効果をつけるかどうか

Midinetteのダイアログ

　パラメータを変えると、ピースの形がある程度変えられるので例えば、こんな風にもなる。ここでは各ピースをバラバラにしている（ちゃんとバラバラにしていないのはご愛敬だが…）。
 

Midinetteの処理画面をちょっとだけ加工したもの　パート２

　ところで、このプラグインが作るパズルのカケラは、本来のジグソーパズルのカケラの形とは違う。本来、ジグゾーパズルでは各のピースはどれも違う形だけれど、このプラグインではどれも同じ形になる。今回のプラグインでは、それぞれのカケラ、ピースを並べ替えたあとでも、どのピースも形の上ではきちんとはまって、きれいに一枚の絵になる方が便利だろうと考えてどのピースも同じ形にしてみた。

　だから、今回のMidinetteが作るパズルのカケラはどの場所に置いてもきちんとはまってしまう。だから
どのピースをどこに置くかはユーザー次第だ。もちろん、元画像がちゃんと再現するように並べてみても良いけれど、それでは元画像そのままだ。それは全然面白くない。せっかくばらばらのカケラにする意味がない。やっぱり、ここは自分の好みにまかせて、それぞれのパズルのカケラを好きな場所に置くべきだろう。

　一旦、元の画像を頼りにならないとなってしまえば、あとはもう別に一つの答えがあるわけじゃないし、もう気の向くまま風の向くまま、「自分の感覚」だけを頼りにして、色々いじればきっと面白いはずだ。頭の中で色んな思考のカケラを並べてみるように、このMidinetteでパズルのカケラを自分の好きなように並べて遊んでみてもらえたら、とてもうれしい。　byぐるぐる
 

■CleType自主学習（仮）　

ちょっと真面目にClearType（仮）

1. 楽しそうな「iMac」＆「電子ブック」風ノートPC用スタンド　-はじまり -　(2002.08.26)
2. 一本道か、分かれ道か　- ドキュメントの縦横比について- (2002.08.29)
3. 水平思考と垂直思考 - 文字の縦横解像度 -　(2002.08.29)
4. 細かくすると楽（粗く）になる？ - ClearTypeの一番の秘密-　(2002.09.09)

楽しそうな「iMac」＆「電子ブック」風ノートPC用スタンド　-はじまり -　(2002.08.26)

　Lapvantageという楽しそうな会社を初めて知った。ノートPCをiMac風にするLapvantageDomeやPCを縦置きで使うためのLapvantagePortraitという、とても実用的でいて、それでいて明和電機のような面白い製品を作っている会社である。明和電機は兄弟が運営しているが、こちらのLapvantageの方はビアボーム親子がやっているらしい。iMac風スタンドの方は角度が振れないようのが（特にノートPCを立てられない）残念だが、Lapvantageの方はもう少しデザインがスマートであるならば今すぐにでも欲しくなる。
 

Lapvantage Products

Lapvantage Dome

Lapvantage Portrait

　複数の作業を切り替えながら作業をしたり、あるいはツールバーが多数出てくるようなソフトウェアを使って作業をする時には、左右に広いディスプレイが便利で使いやすい。しかし、単純に一つのドキュメントを読んだり、一つのドキュメントを書いたりする場合には上下に長いディスプレイを使うと、見通しがきいて考えをまとめやすくなる。気のせいか、頭の中の見通しがとても良くなるように感じたりする。だから、以前から横長の画面のノートPC(ToshibaPortege 320)を愛用していたりした私はノートPCの画面を横にして使ったり、縦にして使ったりと、画面を切り替えて使ってみたいと感じていた。AdobeAcrobat Readerであれば、画面を回転させて文章を読む機能があるので、これまでノートPCを回転させて電子ブックのようにして文章を読んだりすることもあった。　

　Lapvantage PortraitはPivotProのソフトウェア付きなので、Windowsの画面を自由自在に回転させることができる。だから、ノートPCを普通に横置きに使ってみたり、スタンドに載せて縦置きに切り替えて使ってみたり、と好きなように切り替えることができる。「これはなかなか便利そうだ」と思い、私も私も30日有効のPivotProのデモ版をインストールして使ってみることにした。

　そして、このソフトのインストールをきっかけにして

• ファイト！縦文字文化　-縦と横の解像度を考えよう - (2001.04.29)

• デバイスドライバーは仮免-ClearTypeの秘密 - (1999.09.26)

一本道か、分かれ道か　- ドキュメントの縦横比について- (2002.08.29)

　前回書いたように、複数のことを考えるなら「左右に長いディスプレイ」が良くて、一つのドキュメントを読むなら「上下に長いディスプレイ」が良い。その理由を端的に言えば、「目が左右についているから」だと思う。

　まず、「目が左右に付いているので、あまりに大きい左右への目の動きは、目にとってとても非対称な作業であるから不自然」だ。だから、左右を眺めるときには自然と頭を左右に振ることになる。その頭を左右に振るという作業は、頭の中での何らかの切り替え作業を伴うような気がする。だから逆に、ツールパレットの切り替えのような「何らかの作業の切り替え」を伴う作業であれば、その左右へ視線を移動する（自然と頭も左右に動かす）ということはとても自然な行為になる。しかし、それは一つのドキュメントを読むような場合には、いたって不自然な行為になってしまう。だから、一つのドキュメントというのは本来「上下に長い＝縦長」であるべきだと思う。

　そしてまた、「目が左右についているから」、人は上下方向を「一本道」に繋げて考える。例えば、絵画を眺めるとき、上に見える景色は多くの場合遠い景色で、下に見える景色は多くの場合近い景色だ。漱石の文学論の図を引くまでもなく、この「上下の遠さ、距離」というものを例えば時系列上の「一本道」に繋げるのは、いたって自然な連想だと思う。「遠い上」に見えるものは「遠い過去」で、下に来ればくるほど新しいことになる。それは、ドキュメントを読む場合に対応させて考えると、とても自然だ。それに対して、左右に並ぶものは決して「一本道」ではないのである。それは、「選択肢＝分かれ道」であって、決して一つの道ではないのである。左右に並ぶものは「複数の何か」なのである。

　だから、一つのドキュメントは上下に並び、上下に長いべきなのである。ドキュメントの表示も同じく、縦に長いべきなのである。
 

「文学の焦点」

漱石　「文学論」より

　最近のPCであると、ディスプレイは通常横に長い。だから、本来縦に長くあるべきドキュメントを眺めようとする場合には、表示を90°回転させてやることもある。そうすると、本の一ページのようにして画面表示を眺めることができる。例えば、AcrobatReaderで表示画面を回転させたり、PivotProなど使ってPCの画面表示自体を回転させてやれば良いわけである。
 

Acrobat Readerで90°回転表示をする

回転させない場合

回転させた場合

PDF表示を90%回転させている例

縦長のドキュメントを読むことができる

　このように、ドキュメント表示のための縦横比については、単にディスプレイの表示を90°回転させてやれば問題は解決する。しかし、表示のためのもうひとつの条件、表示品質が問題になってくる。そもそも、液晶(二十世紀においてきたCRTは無視しよう)の解像度はまだま低くて、それを改善するための技術としてClearTypeやCool Fontがあるのだけれど、AdobeのCool Typeはともかく、Clear Typeの場合には表示が90°回転しているという情報をClearTypeが取り扱わない（知らない）ために、上手く動かなくなってしまう。ClearTypeにしてもCool Fontにしても、液晶のRGBのカラーフィルターの並び方を利用してやることで解像度を高めているわけで、その並びの変化（表示の回転）に対応できない場合には表示品質を大幅に落とすことになってしまう。

　次に、「ファイト！縦文字文化　-縦と横の解像度を考えよう - (2001.04.29)」で考察した、文字の解像度についてもう少しちゃんと考えてみることにする。

水平思考と垂直思考 - 文字の縦横解像度 -　(2002.08.29)

　ドキュメントを表示させるためには、文字を表示させてやらなければならない。しかし、液晶ディスプレイの解像度は必要十分には高くないから、文字はつぶれてしまうことが多い。例えば、「現実問題春夏雪雹資本主義電計算機」なんて文字を表示させてみるとかなり潰れてしまい、非常に読みにくいのが判るはずである。これが、英語の"RealProblem seasons Snow capitalism Computer"なんて文字であれば、まだマシである。

　この日本語と英語の文字の解像度の差について考えてみる。比較例は下に示した、「漢字」と「英語」のテキストを用いることにする。
 

日本語と英語の文字の解像度

「漢字」

「英語」

　まずは、600dpiで20ptのMS Pゴシックのフォントを展開して上のような画像にした後に縦・横方向のそれぞれの解像度を考えてみる。ここでは、縦・横方向の黒い線（あるいは線でない部分）の太さ（幅）の分布を測ってみることにした(今回解析のために作成したソフトはここ（RunLength.lzh）においておく)。テキストのような二値の画像の「解像度特性」を計測するのであれば、このような解析にしなければならない。「ファイト！縦文字文化　-縦と横の解像度を考えよう - (2001.04.29)」でやったようなフーリエ解析は適切な方法ではないのである。

　下の図が縦・横方向の黒い線（あるいは線でない部分）の太さ（幅）の分布である。縦方向に計測した黒い線（あるいは線でない部分）の太さというのは、結局のところ横線の太さ（あるいは線の間隔）であり、横方向に計測した黒い線（あるいは線でない部分）の太さというのは、結局のところ縦線の太さ（あるいは線の間隔）ということになる。どれだけの細かさで「太さ」（あるいは「位置」）を描いてやらなければならないか、を示すグラフということになる。
 

600dpiで20ptのMS Pゴシックのフォントをビットマップに展開してみた場合

「漢字」の場合

「アルファベット」の場合

　「漢字」の場合には「Vertical 方向で計測した線の太さ（あるいは線の間隔）、すなわち横線の太さ（あるいは線の間隔）」が「縦線の太さ（あるいは線の間隔）」に比べて、大きく小さい方にシフトしていることが判ると思う。また、横線の量が縦線の量に比べてずっと多いことも判ると思う。後者は「数字文字の画像学　-縦書きと横書きのバーコード - (2000.01.21) 」で考えたことと全く同じで、「日本語は横線が多い」ということを端的に示している。そして、前者は「Vertical方向で計測した（すなわち横）線の太さ（あるいは線の間隔）」が縦のそれより大幅に小さいということは、「漢字」の解像度は縦方向に大幅に解像度が高い、ということを示している。漢字は縦書き文字故に鉛直思考志向なのである。

　一方、「アルファベット」の場合には、これも「数字文字の画像学　-縦書きと横書きのバーコード - (2000.01.21) 」で考えたことであるが、縦線と横線の量においてはむしろ縦線の方が多いことが判る。水平方向に対して情報量が多いのである。アルファベットは水平思考志向なのである。「アルファベット」の情報量はそのかなりの部分が縦線によるものなのである。そしてまた、線の太さ（あるいは間隔）は横線の方が細い（あるいは線間隔が短い）が、その横線であっても「漢字」の縦線程度の解像度であることが判る。「漢字」に比べて「アルファベット」の解像度は低いのである。

　ただし、文字の解像度を「線の太さ（あるいは間隔）の最小値」だけで論じることはできない。「適切な線の太さ（あるいは間隔）」にすることができるほどに解像度が十分高いか、ということも重要である。もし、そうでなかったら線が妙に太くなったり、細くなったりしてしまったり、あるいは、線の間隔が妙に近づいたり離れてしまったり、つまりは文字のプロポーションが崩れてしまったりするだろう。上の場合は600dpiで文字を表示させた場合の解析例だが、次に現在の液晶と同じような解像度（例えば）150dpiでこの文字を表示（展開）させてみる。こうすることでことで「適切な線の太さ（あるいは間隔）」にできていない様子を確認してみたい。
 
 
 

細かくすると楽（粗く）になる？ - ClearTypeの一番の秘密-　(2002.09.09)

　まずは、「現実問題春夏雪雹資本主義電計算機」という漢字と"RealProblem seasons Snow capitalism Computer"というアルファベットを現在の液晶と同じような解像度（例えば）150dpiでこの文字を表示（展開）させてみた。そして、前回と同じようにそのビットマップ画像の「縦・横方向の黒い線（あるいは線でない部分）の太さ（幅）の分布」を調べてみる。その結果が下のグラフである。また、前回に調べた、これよりも４倍程解像度が高い「600dpiで20ptのMSPゴシックのフォントをビットマップに展開してみた場合」をさらに下に比較用として示してみる。
 

150dpiの解像度で20ptの文字を出力してみた

「漢字」の場合

「アルファベット」の場合

600dpiで20ptのMS Pゴシックのフォントをビットマップに展開してみた場合

「漢字」の場合

「アルファベット」の場合

　150dpiでTrueTypeをビットマップに量子化した場合には、漢字・アルファベットの場合共に、縦・横方向とも600dpi単位で4,8pixelの太さ＝150dpiで1,2ピクセル幅のパターンが発生していることが判る。このようなパターンは、600dpiで20ptのMSPゴシックのフォントをビットマップに展開してみた場合には見られなかったものである。つまり、、着目すべきは例えばアルファベットの場合、

• 縦方向には幅10pixel(600dpi単位)=2.5pixel(150dpi単位)以下の高い周波数は存在していなかった
• 横方向には幅13pixel(600dpi単位)≒3pixel(150dpi単位)以下の高い周波数は存在していなかった

• 縦・横方向共に幅4,8pixel(600dpi単位)=1,2pixel(150dpi単位)以下の高い周波数が生じている

• 縦方向には幅7pixel(600dpi単位)≒2pixel(150dpi単位)以下の高い周波数は存在していなかった
• 横方向には幅11pixel(600dpi単位)≒2.5pixel(150dpi単位)以下の高い周波数は存在していなかった

• 縦・横方向共に幅4,8pixel(600dpi単位)=1,2pixel(150dpi単位)以下の高い周波数が非常に多く生じている

　また、これらの文字の場合には本来18〜15≒12pixel(600dpi単位)の線幅・線間のパターンが多いわけであるが、それを150dpi単位（　=600dpi単位で4pixel　)で量子化してしまうと、場所により4/12 = 33%もの線幅・線間の位置の誤差が生じてしまうことになる。不必要に狭い幅のパターンが作成されたり、不必要に広い幅のパターンが作成されたりして、これでは文字の線が太くなったり細くなったり、線の位置が狂ったりしてしまい、見にくいことこのうえない。これはすべて、150dpiという低解像度で量子化してしまったためである。「低解像度の表示系の解像度に合わせて量子化（ビットマップ化）してしまうと、ますますその表示系では表示しづらい高周波のパターンが生成されてしまい、結果として読みづらい」という一見逆説的に思えてしまう（しかし当たり前の）現象が生じている。

　ところで、本題のClearTypeの場合には横方向（通常の液晶はRGBの3つのサブピクセルが横方向に並べられているから）の解像度を3倍だと仮想的に考えて、横方向を3倍の解像度で量子化を行うことになる。ここで、話の単純のために3倍≒4倍と思うことにすれば、つまりはClearTypeの場合には本来150dpiの解像度であるにも関わらず、サブピクセルを考えて600dpiの解像度で量子化している、ということである。それは結局上の二つのグラフの比較と同じであって、ClearTypeを使うと実は表示すべきパターンが「より表示しやすい低い周波数のパターン」になっているのである。それは、「文字の線が太くなったり細くなったり、線の位置が狂ったりしてしまう」ことがなく、目にとってはとても見やすいパターンになるだろう。この量子化の段階について触れている情報は見たことがないが、実はこの量子化の段階にClearTypeの隠された（しかし、一番重要な）メリットがあるように思う。また、アルファベットの場合にはHorizontal方向に振幅を持つパターン（＝縦線）が支配的に多いため、Horizontal方向に仮想的に高解像度の量子化を行うことは非常にメリットを効果的に得られると考えるのが自然である。

　次に、このように量子化されたデータをClearTypeで表示する際の問題点・その解決方法について考えてみていくことにしたい。

　P.S.ちなみに解析ソフト（RunLength.lzh）をアップロードしました。