2000-08-13[n年前へ]
■WEBの時間、サイトの寿命 
ゆっくり長く続けましょうか?
以前、
でロゲルギストが- 第五物理の散歩道 ロゲルギスト著 岩波新書 「通信を考える」
- その系の情報処理の単位時間
- その系の信号の伝わる速度
- その系の空間スケール
- 空間スケール < 情報処理の単位時間 × 信号の伝わる速度
- 大人数から構成される企業のスピードは、少人数から構成される企業のそれには遙かに及ばない
ところで、ロゲルギスト達はある系の「単位時間・信号伝達速度・大きさ」の間の関係について、
- 「単位時間・信号伝達速度」を入力値として、「大きさ」を考える
- 「大きさ・信号伝達速度」を入力値として、「単位時間」を考える
さて、寺田寅彦が「単位時間・信号伝達速度・大きさ」について、さらにどのようなことを展開していたかというと、それはある系の「大きさ・寿命」についての関係である。寺田寅彦は
- 空想日録 三 身長と寿命 (寺田寅彦随筆集 第四巻 岩波文庫 小宮豊隆編)
- 人体感覚について振動感覚の限界を調べた実験データ、 - 人は自らの体の固有振動周波数の振動に対してもっとも過敏である- 、というものをきっかけとして、
- 生物の時間の長さの単位は相対的なものである
- ある系の「時間の長さの感覚 = 相対的な単位」はその系の固有周期と密接な関係がある(振り子時計なんてわかりやすいだろう)
- ある系の「寿命」を測る単位は、その系の「時間の相対的な単位」、すなわち、その系の固有周期だと想像してみよう。
- その場合、ある系の固有周期はその系の大きさに比例するから、大きい動物ほどその系の「時間の相対的な単位」は長いものとなり、見かけ上の「寿命」はその動物の「大きさ」に比例するだろう。
なるほど、サイズが小さい動物(すなわち固有振動の波長の短い動物)にとっては、ほんの小さな変化も大きな変化である。ということは、その動物の感じる「時間単位」は短くなければ、生き残れないだろう。逆に、サイズの大きな動物は俊敏な動きはできないわけで、その動物の「時間単位」は長くならざるをえないだろう。
ゾウのような大きい動物は「時間単位」が長く、一見「寿命」が長いように見え、ノミのような小さな動物は「時間単位」が短く、一見「寿命」が短く見えるというわけだ。実は、ゾウもノミもその動物自身の「時間単位」を基準にすると、同じ寿命を生き抜いているということになる。
本川達雄の中公新書「ゾウの時間 ネズミの時間」では- 体重の4分の1乗に比例して「その動物の時間単位=生理的時間」が長くなる-と述べられているが、昭和八年に既に寺田寅彦は体重は身長の3乗に比例する、逆に言えば体重は身長の3分の1乗に比例するから、「体重の3分の1乗に比例して時間が長くなるだろう」と想像を巡らせているのである。素晴らしい、想像力である。
さて、寺田寅彦はロゲルギストと違って、「単位時間・大きさ」については言及しているが「信号伝達速度」については触れていない(その替わり、さらに「寿命」にまで触れているわけであるが)。もっとも、私があえて書き加えてみるならば、ある系の固有振動にはその系の中での弾性が密接に関係するし、弾性はその中での弾性波の速度も密接に関係する。つまり、ある系の固有振動の周期というものには「その系中での波の伝達速度」が暗に隠されていて、寺田寅彦は単にそれを一定とおいていたわけで、寺田寅彦が述べた内容は実はロゲルギスト達の述べた内容を包括している、と私は思うのである。
このような「単位時間・大きさ・信号伝達速度・寿命」に関する話は動物に限るものではない。
- ロゲルギストが「信号伝達速度=光速度」として、「処理速度を確保する」ための人類の行動範囲について論じたり、
- 私(いきなり自分を例に出すのも何だが)が「信号伝達速度の変化」と「大きさ(人口)の変化」から人類の処理速度の変化について論じたり
さて、前振りが長くなった。前回、
では、単に「信号伝達速度の変化」と「大きさ(人口)の変化」を並べて「処理速度」の変化について考えてみただけだった。今回は寺田寅彦が考えたのと同じく、「信号伝達速度」と「大きさ(人口)」から「寿命」が決まると考えることにより、「人類」の「寿命」の変化について考えてみることにしたいと思う まずは、前回使った「人類の大きさ=人口」の変化が次のグラフである。ただし、この人口は全然正確ではないし、むしろかなり不正確なものであることは先に断っておく。ここでは、細かな値を使うのが目的ではないので別に構わないだろう。
 |
そして、「人類」の中での「情報伝達速度」の変化を示したものが次のグラフである。この速度が「人類」という集合体の中での波の進行速度を決めるのである。
 |
それでは、「人類」という集合体の固有振動はどうやって扱うかというと、この
- 「人類の大きさ=人口」
- 「情報伝達速度」
- 人口 / 情報伝達の速度
その、人口 / 情報伝達の速度 = 「人類の固有時間」を計算してみたものを次に示してみよう。
 |
こうしてみると、人類というヒトの集合体においては、どんどん時間の流れは速くなり、それに応じて見かけの「寿命」は短くなっている、ということがわかる。人類はまさに生き急いでいるのである。もし、この流れを止めようと思ったら、どうしたら良いだろうか?それには、今回の計算から言えば情報転送速度を遅くするか、人類の大きさを大きくするしかない。情報転送速度を遅くするのはなんとも後ろ向き(byわきめも)だし、人口を減らすというのもなんとも後ろ向きだ。だとしたら、宇宙へでも人類が進出して、人類の空間的なスケールを大きくしていくしかないのだろうか?これもまた難しい話である。
さて、最近、大好きなWEBサイトが閉鎖してしまったり、更新速度が遅くなっていたりしていて少しさみしい。だけど、もしかしたら各WEBサイトにも、「更新速度が速いと、WEBサイトの寿命が短い」なんて法則が実はあるのかもしれない。更新速度が速いということは、そのWEBサイトの固有時間が速く流れているということで、限られた寿命をどんどん使い果たしているのかもしれない。
だとしたら、更新速度が遅いということはそのWEBサイトの寿命が長くなるということだから、それはそれで良いのかなぁ、などと思ってみたりする。「太くて短い寿命」も「細くて長い寿命」も実は本人からすればどちらも同じ長さなのかもしれないけれど、外から見ている私は「細くても良いから長く続いて欲しいなぁ」なんて思ってもみたりするのである。
2000-09-16[n年前へ]
■モザイク消し器の真実 
買うも買わないもアナタの自由
で「モザイク消し器」について考えてみた。といっても、考えてみただけで使ってみたわけではない。当たり前である。そんな「モザイク消し器」が私の家にあるわけはないからだ。歩く「悟り」、歩く「生き仏」と呼ばれる私の家にそんなものがあって良いはずがない。その証拠に私はそんな風に呼ばれたことがない(土屋賢治風ロジック)。モザイクの向こう - 隠しているから良いのです- (2000.07.18)
さて、そんな風に言いたい所なのだが、実はそれがあるのだ。何と、「モザイク消し器」が私の家には鎮座しているのである。といって、それは私のものではなくて、某編集者の方がとあることのために送ってくれたものなのである。
 |
残念ながら、このくりくり小僧はあまりにも使い物にならなかったので、部屋の片隅にそのまま放置されていた。いや、こう書くと誤解されそうである。別に変なことに使ったわけではなくて、技術的に使い物にならなかったのである。一応、そこの所はハッキリしておきたい。大体、コレを一体どうやって変なことに使うのだ(以下略)。
今回、このくりくり小僧を送り返すことになったので、せっかくだからこのモザイク消し器がどんな風に技術的に使い物にならなかったかをこのタイミングで書いてみることにしたいと思う。
まずは、このくりくり小僧の操作方法を説明しておこう。ビデオ信号は通常のNTSC信号で入出力するようになっている。エロビデオをこの「くりくり小僧」に入力し、処理した画像をテレビへ送るのである。あるいは、処理した画像を新たにビデオにダビングするのかもしれない。
この「くりくり小僧」は、対応するモザイク処理(広義の)の種類は
- モザイク(狭義の)
- 反転
 |  |  |
「くりくり小僧」の写真を見ると判ると思うが、画像復元処理をかける領域の
- 大きさ
- 位置
写真中にあるその他のボリューム
- 輝度
- 明るさ
- エンハンサー
それでは、まずは適当にモザイク画像を作ってみる。そして、その画像を「くりくり小僧」を使ってキレイに戻せるかを調べてみることにしよう。そこで、最初に示すのが
- 女性のオリジナル画像
- オリジナル画像の一部に反転処理をかけたもの(後述するが、実は失敗している)
 |  |
上の右の反転画像の中央部に対して、「くりくり小僧」で復元処理をかけてみたのが下の画像である。さて、画像は元通りになっているだろうか?
 |
この画像を見る階調は確かに反転しているのであるが、色が明らかにおかしい。オリジナル画像では赤かったハズの唇が青いのである。それどころか、顔全体が青いのである。真っ青だ。明るさは正しそうなのであるが、色合いは絶対に何かが狂っている。
そこで、「基準画像」に対して、「くりくり小僧」で反転復元処理をかけてみることで、どのような処理をかけているかを調べてみた。それが下の画像である。左が「基準画像」で、右が「基準画像」に「くりくり小僧」で反転復元処理をかけてみた画像である。なお、画像の右端および下端部分に関しては「くりくり小僧」で反転復元処理をかけていない。
 |  |
さて、画像の向かって左にあるグレイスケールの階調部分を見れば一目瞭然だと思うが、この「くりくり小僧」で反転復元処理をかけた画像は確かに明るさが反転している。それはその他の白黒画像の部分を見ても明らかである。
そして、カラーチャート部分を見てみると、色合いは実は全く変化していないことが判る。右上から左下まで「紫・青...橙・赤」と繋がっているカラーチャートは左と右でそれほど違っていない。ほとんど同じである。
それは考えてみれば、当たり前なのである。「くりくり小僧」の入出力はNTSC(NationalTelevision System Commitee)方式を使っている。このNTSC信号はカラー画像を
- 輝度情報
- 赤 - 輝度情報
- 青 - 輝度情報
- 赤 - 輝度情報
- 青 - 輝度情報
ところが、先ほど私が女性のオリジナル画像に対して反転処理をかけてみたものは、RGB画像のRGBそれぞれのチャンネルに対して反転処理をかけていたのである。これでは、明るさが反転するだけでなくて、色合いまで反転してしまう。私は、何と「くりくり小僧」の入出力はNTSC方式を使っていて、RGB画像でないことを失念していたのである。その結果、女性の顔色が反転したまま真っ青になってしまったわけだ。
そこで、その「輝度チャンネルのみの反転」ということを考慮してテストしてみたものが次の画像である。今度は反転画像の中央部に「くりくり小僧」で復元処理をかけた部分の色合いが正しい色合いであることがわかるだろう。
 |
なるほど、「反転画像」に関しては「くりくり小僧」は確かにちゃんと画像を復元できることが判った。しかし、しかしである。反転モザイク処理をかけたビデオなんてそうそうあるわけがない。いや、そんなに自信を持っていうと何やら変な疑いをかけられそうであるが、多分そうだろう。ほとんどは、次に示すモザイク(狭義の)処理だと思う。それをキレイに復元できなければ、「モザイク消し器」と名乗る資格はない。そうは思わないだろうか?百歩譲っても、「反転消し器」と言うべきではないだろうか?そこで、狭義のモザイク画像に対してこの「くりくり小僧」が威力を発揮することができるかどうかを、次に調べてみた。
まずは、作ったモザイク画像を先に示そう。下の左が先程と同じオリジナル画像で、右がモザイク(狭義の)画像である。よく(?)見かける画像だと思う。
 |  |
それでは、「くりくり画像」はこのモザイク向こうをキレイに映し出すことができるだろうか?この機械は悩めるエロ子羊達を救うことができるのだろうか?それを確かめてみたのが次の画像である。先のモザイク画像の中央部に「くりくり小僧」で復元処理をかけてみたものである。
 |
「何だこりゃぁあぁ」、と私は思わず叫びそうになった。いや、別にこの機械のためにお金を払ったわけじゃないから良いのだけれど、一体なんなのだこれは。このモザイク消し機能はハッキリ言って大嘘である。桃太郎侍だったら「おまえなんか「モザイク消し器」じゃねぇぇ」と切り捨てるところだ。
これなら、前回
で試したような単なるボカシ処理の方がずっと上である。ちなみに、この下の画像が単なるボカシ処理で「モザイク」を消してみたものである。上の「くりくり小僧」の復元画像よりもずっとマシであることが判るだろう。モザイクの向こう - 隠しているから良いのです- (2000.07.18)
 |
ちなみに、先程の「反転処理」の場合と同じように、「基準チャート」に対して「くりくり小僧」でモザイク復元処理をかけてみたものを示してみよう。下に示すその画像を見れば、「くりくり小僧」のモザイク復元処理が
- 輝度チャンネルの反転処理
- 横方向のエッジ強調処理
 |  |
しかし、この「モザイク復元処理」をかけてみても、私には全然モザイクの向こうは見えないのである。もう、何が何だか判らないのである。もう、何が何だか判らないが故に、もしかしたら人の持つ無限の想像力をフルに発揮できるのではないか、と思うほどである。私は残念ながらエロの想像力が足りないのかもしれないが、想像力の発達したエロの天上人達であれば話は別だろう。
さて、今回の話は「モザイク消し器のMTF(仮称)」というタイトルで書き始めたのであるが、「モザイク消し器」の実力がこんなものだったのでお蔵入りしていたのである。まぁ、解析の出来としてはイマイチであるが、もしかしたら「モザイク消し器」を買おうかどうかと迷っている子羊達の参考になるかもしれないので、一応公開してみた次第だ。
さて、私はこの機械をいじってみて思わず暴れ出しそうになったが、それはもしかしたら私だけかもしれない。人によっては、「何て素晴らしいんだ!!この機械は!!」と感激する可能性だってゼロではない。イマジネーションが豊かなあなたであれば、さぞかし素晴らしい桃源郷がモザイクの向こうに見えるのかもしれない。
だから、「買うか、買わないか」はアナタの自由だ。だから、このイマジネーション養成ギブスに大枚を払うの悪くないかもしれない。この機械でイマジネーションを鍛えた暁には、モザイクの向こうにアナタには何かが見えるかもしれない。確かに、それも悪くないかもしれないだろう。そこに何が見えるかは、結局あなた次第だと思うのである。
2001-01-21[n年前へ]
■カンバスから飛び出す「名画の世界」 
作者の視点から眺めてみれば
先日、新穂高ロープウェイスキー場へ行った。雄大な景色に囲まれたとても素晴らしいスキー場だ。その景色を思わずデジカメで撮ったのが下の写真である。まずはこの「写真をじっくりと眺めて」みて欲しい。
 |
私が感じた「雄大な景色」は伝わっただろうか? きっと私の感じた「雄大な」感じは百分の一も感じられないに違いない。それでは、次に片目をつむって、もう片方の開いた目だけでこの写真をもう一度眺めてみてもらいたい。そうすると、今度は一体どんな風に感じられるだろうか?今度は、立体的に浮かび上がる山と谷が浮かび上がってくるハズである。
この「片目で写真を眺める」というのは南伸坊の「モンガイカンの美術館」の中で書かれている「写真の見方」である。その一部分を引用してみると、
ヒトの視覚の特殊性というのは、横に並んだ二つの目が、それぞれ違った映像を感じて、それが脳ミソでかきまぜられて、立体を感じるようになっていることなのだった。私はこれを初めて読んだときは、目からウロコが落ちたような気持ちになった。それまでは、私は写真を「じっくりと眺め」ようとして、両目でじっくりと眺めてしまっていたのである。両目、すなわち、作者とは異なる視点からじっくりと眺めてしまっていたのである。写真に切り取られている景色は作者の視点・場所から描かれているのだから、その場所からじっくり眺めてみれば、もっとそこに切り取られている世界を感じることができたに違いないのだが、そこをちょっと勘違いしていたわけだ。一方、カメラというのは、もともとが片目で見た映像なのである。ファインダーをのぞいていないほうの目を、カメラマンがあけたままであっても、写ってきた写真は片目の映像には違いない。これを両目で見れば、「写真は立体を平面に置き換えたものである」という正論が見えてしまうばかりである。だから、写真を、実物からうける視覚の印象と同じように見ようとするなら、片目で見なければいけないのである。
映画のセットは撮影しているカメラの位置から見るのが正しいのであって、それ以外の位置から見ても意味がない。違う角度から見てみても、それはあまり面白くないのである。いや、もちろん映画村とかユニバーサルスタジオとかそんなのも繁盛しているくらいだから、実は裏側から見るのも面白いのだろうが、それはあくまで表から見終わった後での、「裏の眺め」なわけだ。
そういったわけで、写真を眺めるときには「(作者と同じ)片目でじっと眺める」のが良いわけであるが、それは写真だけに限らない。平面に描かれたものであればそれは何だって同じである。普通の絵画だって、版画だって、もう何でもそうだ。例えば、このモネの「散歩、日傘をさす女」を両目と片目で眺めてみよう。これはモネが家族を光り輝く景色の中で描いた名画である。
 |
両目でじっくり眺めてしまうと、いまひとつ感じられない風の感じや空気の透明感が、片目で眺めると躍動感と共にあなたの目の前に迫ってくることと思う。片目でこの画を眺めるとき、私達の目はセザンヌが「彼(モネ)は眼である。しかし、何という眼だろう。」と評したモネの目と一体化し、モネが眺めた景色を私達も眺めることができるのだ。
というわけで、写真に限らず平面に描かれたものであれば、私は片目で作者と同じ視点に立って眺めてみるのが面白いと思うわけだ。平面に描かれた写真や絵画には、作者の片方の目から見た視点しか描かれていないので、私達も同じように片目で見てやればあとは私達の想像力が作者のもう片方の視点を作りだし、作者の感じた世界を立体的に感じることができるのである。
と、そんなことを新穂高ロープウェイスキー場のリフトの上でぼぅ〜と考えていると、少し面白いことを思いついた。平面に描かれた写真や絵画には、作者の片方の目から見た視点しか描かれていないのであれば、もう一つの視点を想像して、そのもうひとつの視点から眺めた情報を絵画に加えてしまえば良いのである。
簡単に言えば、オリジナルの画に描かれている物体の距離に応じて、左右の視差をつくってやった二枚の画像を作れば良いのである。そして、その二枚の画像を左右の目で眺めてみれば、作者が同じく左右の目で眺めている景色、作者が描こうとしたものを眺めることができるかもしれない、と思ったのだ。もちろん、その処理にはいくつかの面倒なこともあるのだが、その処理の細かい内容・注意についてはまた次回以降に説明してみることにして、今回はまずはそういう処理をしてみた名画を見ていくことにしよう。
というわけで、これが作者の視点情報を勝手に加えて3D化したモネの「散歩、日傘をさす女」hirax.netEdittionである。この二枚の画像を平行法、つまり右の絵を右の目で眺めて、左の絵を左の目で眺めてみたならば、キャンバスの中で佇んでいる妻カミール・モネと息子ジーンが、キャンバスの中から浮かび上がってくるはずだ。その時、二人の背景の青い空もより深く見え、空気の透明感も流れる風が流れる時間と共に浮かび上がってくるのである。
 |  |
このThe Stroll, Camille Monet and Her Son Jean hirax.net Edittionを眺めれば、あなたもモネの視点から、彼の両目に映るカミール・モネを感じることができたことと思う。平行視が苦手な人は目の力を抜いて、ゆっくり挑戦してみてもらいた。平行法のコツはぼぅ〜と遠くを眺めるように、目の力を抜くことである。
この「散歩、日傘をさす女」は単に紙で作ったニセモノのパノラマの景色みたいに見える、という人がいるかもしれないので、次にシャガールの「窓」も同じように眺めてみよう。まずは、オリジナルの「窓」である。
 |
そして次が、作者の視点情報を勝手に加えて3D化してみたシャガールの「窓」hirax.netEdittionである。これも同じく、平行法で描かれている。シャガールが眺めている窓の向こうの景色、世界が深い奥行きと共に目の前に出現するハズである。
 |  |
さて、写真にせよ絵画にせよそれは作者の視点から世界を切り取ったものである。その「切り取る」という作業は、このシャガールの絵のタイトルではないが、"window"=「窓」そのものである。限られた「窓」によって画家の感じた世界の一部がカンバスの上に切り取られる。それは逆に言えば、カンバス上に画家の感じた世界へ開かれた「窓」が開いている、ということでもある。
もちろん、私達の視点は必ずしも作者の視点とは同じでないし、作者が世界を切り取った窓もごく限られた小さな窓だろう。だから、なかなか作者が感じた世界を共有することはできないだろう。しかし、作者の視点を想像しながら、作者の切り取ったごく限られた窓に立って外を眺めてみる時、きっとそこには描かれている世界は生き生きと見えてくるに違いないと思うのである。
2001-02-11[n年前へ]
■もう一つの目から眺めた世界 
hirax.net式「平面画像立体化法」
先日、出張のついでに本屋で野田秀樹の「20世紀最後の戯曲集」を買った。電車の中で冒頭の「RightEye」を読んでいると、こんな台詞があった。
オレはもう二度と、立体写真を見ることができない。立体星座早見盤とか、アトラス立体地図とか、ああいうのが見れなくなるんだぞ。「Right Eye」は野田秀樹自身の右目失明、カンボジアで亡くなったカメラマン一ノ瀬泰造、被写体を執拗に追いかけるパパラッチ達、そして死んでいった一人の女性が姿形を変えながら絡み合っていく話だ。
立体写真を見ても立体感を感じるかどうかは人それぞれであるし、空にかかる虹を眺めてみてもそれが何色に見えるかはやはり人それぞれだろう。「平面画像を立体化する話」の話を書いてみても、それを眺めることができない人もいるし、Photoshopを使った話を書いてもPhotoshopを持っていない人には面白くないだけかもしれない、そしてオッパイ星人の話を書けば(いつもバストを大きくしがちなのは、わかりやすさの都合上だったりするだけなのだが)、それで不快になる方も多々いることだろう。
それでも、今回も立体画像の話、「平面画像立体化」の続きを書く。
さて、こんな平面画像があったとしたら、どのようにしてやれば立体化することができるだろうか?
 |
人間が立体感を感じる大きな手がかりの一つが両眼視差だ。遠くにあるものを眺める時には、右目と左目にはほぼ同じように見えるが、近くにあるものを見る時は右目と左目の場所が違うため、右目と左目では違う景色が見えることになる。例えば、下の図のように緑色の○が遠くにあって、青色の□が近くにあった場合を考えると、緑色の○は右目からも左目からも同じように見えるが、青色の□は左目からは視界の右側に見えるし、右目からは視界の左側に見える。
|
この左目と右目からの見え方の違いを頼りにして、立体感を得るのが両眼視差である。であれば、左目用と右目用に別々の画像を用意してやり、その位置のズレを意図的に作ってやれば立体的に見ることができるわけだ。
例えば、下の画像のように青色の□を右へずらしてやり、これを左目用の画像に使えば、立体感を得ることができる。
 |
下の画像はそのようにしてやることで、一番最初に示した図を立体的に見えるようにしたものである。この図は平行法= 「左目で左図を見て、右目で右図を見る」なので、遠くをぼう〜っと眺めるつもりでこの図を眺めれば、きっと青い□が近づいて見えて、この図が立体的に見えるようになるハズだ。
 |
こういった方を用いれば、立体画像を作ることができるわけで、実際「立体星座早見盤」というようなものはそういうやり方で作成されているわけではある。
だが、実は一般的に「平面画像を立体化しよう」とすると、話はそう簡単ではない。それは、こんな図を立体化しようとする場合を考えてみればわかると思う。
 |
「さっきと同じで、青い□の位置をズラしてやれば良いんじゃないの?」と簡単に言う人は少しばかり考えが足りない人である。ちょっとでも考えてみさえすれば、大きな問題に気付くハズである。この図のように背景がある場合には、青い□の位置をズラしたら、そのズレた部分は一体どうしてやれば良いのだろうか?
 |
この部分に何があるかは判らない。だとしたら、単純に青い□の位置をズラすわけにはいかない。考えてみれば、そもそも一つの目から見た情報しかないのだから当たり前なのである。もう一つの目から見た時の情報は我々の手元には無いのである。そこの部分をどうしたら良いかは我々にはわからないのである。
しかし、そうは言っても立体化するためにはこの青い□の位置を左へズラしたい。だけど、位置をズラしたらその部分が真っ白になってしまう。だけど、やっぱり立体化したいからズラしたい。"Toshift it or not to shift it; that is the question."というわけで、これはもうハムレットの心境のようになってしまう。このジレンマを解決してやらなければ、背景がある、あるいは距離の異なる物体が視野の中で重なっている平面画像を立体化することはできないのである。
そこで、「できるかな?」ではそのジレンマを解決するために、単に位置をズラすのではなくて、青い□を拡大しつつ位置をズラすというやり方を考えてみたのである。名付けて、hirax.net式「平面画像立体化法」だ。
例えば、上の画像の場合だとまずは青い□を拡大して、その後右へズラすのである。
 |
上の絵を見ればわかるだろうが、青い□を拡大してやると、元の図形と重心は同じだが、その周りに青い□が拡大することになる。そこで、その拡大した分だけであれば、位置をずらしてやっても背景の画像情報が無い場所が露出してしまう、ということがなくなる。このhirax.net式「平面画像立体化法」はつまり、隠された部分が部分的に露出してしまうのを防ぐために、それ以外の部分を隠してしまうというテクニックなのである。
そのようにして、先の一枚の平面画像を立体化すると下の図のようになる。
 |
前回作成したシャガールの「窓」hirax.net版などはそのようにして作成したものである。この画像の場合は窓枠部分は全く同じなのであるが、窓の中の景色を拡大後、左右の目用の画像をそれぞれ左右にズラしている(ズラし量は高さによって変えている。すなわち景色の中で遠くの部分と近く区の部分ではズラし量を変えている)のである。だから、よくこれらの画像を眺めてみれば、景色部分はオリジナルよりもhirax.net版は大きくなっているし、絵の中に描かれている情報自体もむしろ減少していることがわかると思う。
  |
 |
まずは、hirax.net式「平面画像立体化法」の原理がこの「画像の一部を拡大してからズラす」ということなのである。このやり方でシャガールの「窓」のような絵は立体化してやることができる。
しかし、多くの人が気付くと思うがこれだけではまだまだ不十分なのである。最初の例えのように、四角や丸の形状の物体だけがある場合などはこれで十分なのだが、一般的にはさらなる問題が発生するのである。シャガールの「窓」の場合には、窓枠がほぼ四角と丸の組合わさったような形状をしているために、その問題は発生しないのであるが、一般的な形状の場合には話はそう簡単にはいかないのである。そんな場合、すなわち四角や丸の形状の物体だけで画像が構成されていない場合には、どんな問題が発生し、それをどんな風に解決していくことができるか、については次回以降に考えてみることにしたい。
さて、冒頭で読んでいた「Right Eye」の中の「立体写真を見ることができない」という台詞はこんな感じのカメラマンに対する台詞で続けられていく。
この写真を撮った奴らは、右目(Right Eye)をなくしてる。立体感がない。正しい(=right)右目と、覗きたい左目とのバランスを失っている。物を捉える立体感をなくしたままだ。この台詞を眺めていると、前回の話を読んだ人であれば、その中で引用した南伸坊の「モンガイカンの美術館」の中で書かれている「写真の見方」の文章をきっと思い出すことだろう。
一方、カメラというのは、もともとが片目で見た映像なのである。ファインダーを覗いてないほうの目を、カメラマンがあけたままであっても、写ってきた写真は片目の映像には違いない。つまり、立体感を失った平面画像を眺めるときには、カメラマンあるいは画家と同じように覗きたい片目だけで覗かなければならないのであった。そして、その平面画像に奥行きを与えもう一度立体画像にしてやるためには、hirax.net式「平面画像立体化法」ではないが、違う場所から眺めたときに「姿を現してくる隠されたもの」についてどう対応するかということを考えてやらなければならないと思うのである。
これを両目で見れば、「写真は立体を平面に置き換えたものである」という正論が見えてしまうばかりである。だから、写真を、実物からうける視覚の印象と同じように見ようとするなら、片目で見なければいけないのである。
それは、片目で平面画像を眺めて、そして頭の中でその立体感を与える作業をしてやっても良いかもしれない。また、両目を開けて考えてみても良いかもしれない。ただ、ファインダーを覗いてないほうの目で景色を眺めようとする時には、見えていない景色を想像したり、考えたりする必要があると思うのである。その想像力は、ある意味義務でもあるし、また貴重な自由でもあるのかもしれないなと、電車の中で、ドアに寄りかかりつつ「RightEye」の最後の台詞
のこされた(=left)ものは、のこされた瞳(left eye)で、のこされた夢を見続ける義務がある、… いや自由があるを眺めながら、そんなことを考えてみたりした。
2001-09-12[n年前へ]
■オッパイ星人の力学 求む未来のヒロイン編 
タックルがおいっぱい。
いつでも、正義の味方は人知れず戦い続ける。それが正義の味方だ。…ワタシもその例に漏れず、日夜オッパイ星人と戦い続けているのは周知の通りである。「継続は力なり」というが、はや一年以上もその苦しい戦いは続いている。戦況は必ずしも良いとは言えず苦戦をし続けているが、とにかくワタシはオッパイ星人と死闘の最中なのである。
その苦しくも長いオッパイ星人達との死闘の歴史をちょっとばかり振り返ってみると、
- オッパイ星人の力学 - 胸のヤング率編- (2000.06.29)
- 続 オッパイ星人の力学 - 揺れる胸の動き編- (2000.07.02)
- 続々オッパイ星人の力学 - 胸を揺さぶるパラメータ励振編-(2000.12.01)
- オッパイ星人の力学 第四回- バスト曲線方程式編- (2001.01.13)
- オッパイ星人の力学 仏の手にも煩悩編- 時速60kmの風はおっぱいと同じ感触か? - (2001.01.27)
- オッパイ星人の力学 あなたのオッパイ星人度編- 擬似オッパイに関するhiraxの関係式 - (2001.05.20)
しかし、そんな死闘を続けているのは何も私だけではない。確かに、オッパイ星人をはじめこの地球上には異星人達があふれている。いや、もしかしたら、オッパイ星人と戦う私のような正義の味方はヤツらより数は少ないかもしれない。が、決してワタシは孤独な戦いを続けているわけではないのである。数少ない正義の味方達は日本中の各地で日夜戦い続けているのだ。というわけで、今回はそんな正義の味方達の戦いを、これまでのワタシの戦いと重ね合わせながら紹介してみたい、と思う。
先日、素晴らしい論文(いや違う戦闘報告だ)を見つけた。それは日本人間工学会関西支部大会講演論文集Vol.2000Page. 112-115に掲載されている岡部氏らの「歩行に伴う乳房の振動分析」という報告である。内容は、
着心地の良いブラジャーを設計するためには、乳房の形態を詳細に捉え、動的な挙動を明らかにする必要がある。そのため、歩行中の乳房の振動を、胸部土台の動きから分離・抽出し分析した。歩行中、乳房は複雑な振動を繰り返し、被験者により、また乳房の場所により異なる振動を示すことが判明した。特に、乳房の柔らかさによって振動の特性が大きく異なった。また、同じ乳房上でも柔らかさの違いが振幅と相関を示した。一方、場所が異なると振動に位相差が生じ、これが円運動・8の字型運動の発生につながることが判った。というものである。この戦いの詳細はオリジナルの文献を読んでもらうことにして、私のこれまでのオッパイ星人との戦いと彼らの戦いはかなり似通ったところがあるので、それらを重ね合わせながら彼らの戦いを紹介したい、と思う。そして、それらの似たような過去の戦いを学ぶことで、さらなるオッパイ星人達との戦いに備えたいのだ。いわば、ちょっとした反省会をしてみたいのである。
 |
ワタシはこれまでオッパイ星人達と戦い続けてきた。しかし、その戦いの中で大きな悩みが一つだけあったのである。それは、ワタシが女性達を守るために戦っているにも関わらず、その女性達にワタシがどうも信用されていないフシがあることだった。「オレは味方だぁ」といくら力説しても、「ふぅ〜ん(どうだかねぇ)」と冷たい目でワタシを見る女性が多かったのである。いや、正直に言えばそうでない優しい眼差しを向けてくれる女性など皆無であったのだ。
だから、、「オッパイ星人」達が目を常にロックインさせている「揺れ動くオッパイの動き」を調べようとしても、地球を守るための貴重な被験者になってくれる女性などいるわけもなく、ワタシの戦いはもっぱら計算上のモデルを主戦場としてきた。だから、そんなワタシの戦いを「机上の空論にすぎない」と言う方がいたり、「それって、単なるエッチな夢想ですか?」と言う人がいたり、はたまた「アナタは本当のオッパイを知らない」などと、ワタシは常に罵詈雑言を浴びせられてきたのである。「机の上がダメなら、どこの上なら良いんだぁ〜」とか、「想像力と好奇心が旺盛でどこが悪ぃ〜」とか、「余計なお世話だぁ〜」とか言いたくなるほど、世のため人のために戦い続ける正義の味方に世の中はとても冷たかったのである。
そしてまた、FBIなどが犯罪者と戦う際によく用いる「おとり捜査」というような戦術も協力者がいないため、ワタシは遂行することができなかった。というわけで、「オッパイ星人」をワナにかけて退治しよう、なんていうことはとてもじゃないができなくて、ワタシの戦術はもっぱら専守防衛のみ、という状態だったのである。まるで、日本が誇るセルフ・ディフェンス・アーミーのような状態だったのだ。
しかし、世の中にはそんなワタシのような情けない正義の味方だけではなくて、華やかな戦いを続けているグループもいるのであった。その良い例が先の素晴らしい論文(いや違う戦闘報告だ)を報告した岡部氏らのグループである。何しろ、彼らには年齢22〜23歳の成人女性12名が被験者として協力してくれているのである。仮面ライダーでさえ味方の女性はタックル一人しかいなかったし、五人もいるゴレンジャーの中でさえ仲間の女性はモモレンジャーただ一人しかいなかった。なのに、彼らには12人もの女性の協力者がいるのである。素晴らしくゴージャスなのである。人数で言えば、まるで「モーニング娘。」程のタックルがいるのだ。
しかも、かの戦闘報告にはより詳細なタックル達の紹介文までついており、それによれば
- Bカップの65 1人
- Bカップの70 4人
- Cカップの65 1人
- Cカップの70 4人
- Cカップの75 1人
- Dカップの75 1人
ちなみに、そのオッパイの柔らかさ測定に用いられた測定器は日本電産シンポ(株)製のデジタルフォースゲージである。 …ワタシも硬さの測定をたまに仕事でするので、フォースゲージを使うこともあるのだけれど、これまでこんな測定はしたことがない…。う、うらやましい。
 |
|
このフォースゲージを製造している日本電産シンポも - 各種「力」の計測に対応-と書いてみても、まさかオッパイの弾力の計測に使われるとは思うまい。まさか、異星人「オッパイ星人」との正義の戦いの武器に使われるとは思わなかっただろう。きっと、それを知れば日本電産シンポも正義の誇りに奮い立つハズなのである。
もちろん、先の素晴らしい論文(いや違う戦闘報告だ)には、その正義の武器デジタルフォースゲージを用いた「オッパイの弾力の実測データ」も掲載されており、それが下のグラフだ。
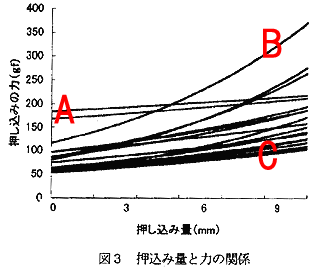 (赤文字はワタシが記入) |
横軸がフォースゲージをオッパイへ押し付ける「押し込み量」で、縦軸はその押し込んだ指プローブをオッパイが「押し返す力」である。このグラフから判るように、オッパイを押し込めば押し込むほど押し返す弾力は強くなるわけだ。もちろん、どんどん押し込めば土台としての肋骨があるハズなわけで、いずれ硬い肋骨にぶつかって「押し返す力」は限りなく大きくなってしまうハズである。その良い例がデータBであって、1cmも指プローブを押し込めば土台としての肋骨に突き当たっているかのようである。
しかし、片やデータAやCのようにその程度押し込んだだけではまだまだ押し返す弾力が強くならない、言い換えれば懐の深さ(それを単に巨乳といってはイケナイ)を感じさせるものも存在するのである。このようなデータを眺めるとき、我々は何が何でも構造解析をしてみたい、と思うのは至極当然のことであろう。
また、面白いことに例えば前回考察した「走る車の窓から出した掌が受ける力とオッパイ一個あたりの重さ(g)を重ね合わせたグラフ」などとこのグラフを並べてみると、まぁまぁ良い感じで力のオーダーが一致していることがわかる。つまり、単なる前回考察したような数値、ワタシが苦しくも続けてきた戦い、は必ずしも「机上の空論」ではなくて、年齢22〜23歳の成人女性12人のタックル達の貴重なデータと割合良い一致し、無駄ではなかったことが確認できるのである。また、ワタシも彼らも「グラム重」を単位として採用していることも確認して頂きたい。
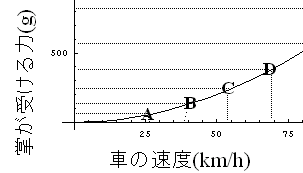 |
そしてまた、彼らはタイトルにもある通り歩行時にタックル達のオッパイの揺れるさまも実測しており、ワタシが続オッパイ星人の力学 - 揺れる胸の動き編 -などで計算し続けてきた歩行時の女性のオッパイの動きとも比較することができるのである。
例えば、その二つを並べたものが下の二つのグラフである。左が実測されたオッパイの揺れるさまであり、右がワタシが計算したGカップバストの女性のオッパイの動きである。
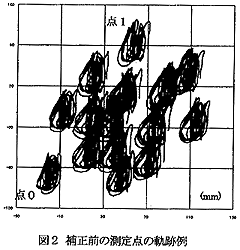 | Gカップバストを揺らす女性のオッパイの動き  |
これらを並べてみると、実測値の方が比較的単純な動きであるのに対して、右側のワタシの計算値の方はずいぶんと複雑になっているが、これはワタシの考えではカップの大きさの違いとオッパイの振動の減衰の仕方が異なるせいだと考えている。比較的小ぶりなバストでは単純な動きですむのであるが、ワタシの試算ではバストが大きくなると動きは急激に複雑になるのである。また、ワタシの計算はオッパイを比較的単純な弾性体として取り扱っているが、本来柔らかいオッパイはそういうものではなくて、オッパイ星人の力学第四回 - バスト曲線方程式編-で挑戦し始めたような水風船モデルで取り扱い、さらにその中でエネルギーの減衰も組み込む必要があると思うのである。
次に、歩く速さを変えたときの実測値と計算値を比較してみる。まずはゆっくり歩いた時のオッパイの振動のようすである。なお、実測値の方は水平方向と鉛直方向の揺れとが分離され表示されている。
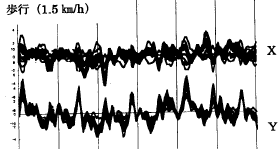 | Gカップバストの軌跡 (1秒で2歩の場合) 横軸 : 左右(cm) 縦軸 : 高さ(cm)  |
これを眺めると、実測値、計算値のいずれにおいても水平方向と鉛直方向にそれほど相関が無い複雑な動きをしていることがわかるだろう。何と言うか、言葉にはできないがアッチコッチアッチコッチぐるんぐるんな状態なのである。
それに対して、速く歩いた場合には結構単純な揺れ方になってくる。それを示したのが下のグラフである。実測値では水平方向と鉛直方向の動きが比較的相関が高そうなことが見て取れるし、右の計算値では一目瞭然ユッサユッサと単純かつキレイな動きになっているのである。
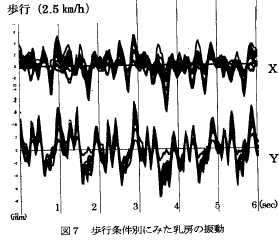 | Gカップバストの軌跡 (1秒で6歩の場合) 横軸 : 左右(cm) 縦軸 : 高さ(cm) 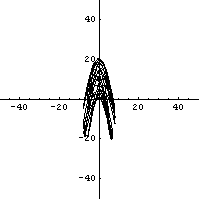 |
このように素晴らしい実測データとワタシのこれまでの戦いを比較してくると、「ワタシの戦いも必ずしもムダではなかった」と思えてくるから不思議である。そして、見たいの地球を守るためにワタシはさらに戦い続けることを誓うのである。
しかし、やはり実測があっての計算である。オッパイ星人を始めとする異星人達の攻撃にさらされている地球を確実に守るためには、ワタシのこれまでの「専守防衛」作戦だけではなくてもっと攻撃的な布陣や戦略を活用したいところだ。そのためには、ワタシと一緒に未来の地球を守るタックル達の結集を強く望む(自衛隊のポスター風に)次第であると一応書いておいて、今回の反省会を終了したいと思う。

