2012-04-16[n年前へ]
■エクセルで２次方程式の「解の配置」を図示してみる!? 
（たとえば）２次方程式、つまりx^2+bx+c==0という方程式の実数解を、中学生か高校生の頃、グラフにしてよく眺めたような気がします。しかし、それらの方程式がいつも１個か２個の解を持つにも関わらず、グラフにして眺めるのは「（時にはゼロ個の）実数解」だったような気がします。
そこで、今日は「複素数係数を持つ２次方程式の（複素数）解を”可視化する”エクセルシートを作ってみました（ダウンロード先）。"b"と"c"という２つの複素数を入力すると、（ある程度の範囲の）任意の複素数を"x"とした上で"x^2+bx+c"を計算し、その計算結果がゼロ近くになる部分（どんな複素数値を”ｘ”に代入すれば"x^2+bx+c"という式がゼロになるか）を複素平面上で”可視化”する、というエクセルシートです。
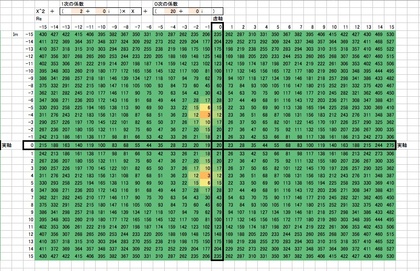
実数（あるいは時に複素数の）係数b,cを持つ２次方程式の、それら係数b,cを自由自在に動かしてみた時の２次方程式の２つの解（の配置や動き方）を眺めてみると、何だかとても面白いものです。たとえば、実数係数の２次方程式を作った時には、実数軸に線対称な２つの共役数が解になったり、複素数係数を入れてみると…何だか綺麗な対応が見えてきたり…と不思議に魅力的な世界が見えてくるのです。
明日は、「係数」をドラッグ＆ドロップで動かすと、「解」がどんな風に・どんな配置で動き回るかでも眺めてみよう（眺められるソフトでも作ってみよう）と思います。
」など。